机器学习——评价指标

机器学习——评价指标

1、结果统计

1.1 混淆矩阵表示

	正样本	负样本
正样本	True Positive(TP)	False Negative(FN)
负样本	False Positive(FP)	True Negative (TN)

TP：将正样本识别为正样本的数量或者比例
FN: 将正样本识别成负样本的数量或者比例
FP：将负样本识别成正样本的数量或者比例
TN ：将负样本识别成负样本的数量或者比例

1.2 准确率，精确率和召回率

准确率：
$$Y=\frac{TP+TN}{TP+TN+FP+FN}$$
表示所有的样本被分类正确的概率。
精确率(查准率)：
$$P=\frac{TP}{TP+FP}$$
在所有识别出来的正样本中，真正为正样本的概率。

召回率(查全率)：
$$R=\frac{TP}{TP+FN}$$
在所有的正样本中，被准确识别的概率。

准确率和召回率是一对相对矛盾的度量，一般情况下，精确率越高的时候，召回率越低。也就是说，我们如果想要提高召回率，那就需要增加样本分类为正的数量，如所有的样本的分类均为正，那么精确率自然的提升了，因为所有实际上为正的样本均被识别成正样本。但是这难免会增加FP的值，也就引起了精确率的降低。

1.3 多数据集下的相关指标

当我们用一个模型去训练多个数据集的时候，会产生对个混淆矩阵。或者，在一个数据集上训练测试多次的时候，也会产生多个混淆矩阵。当产生多个混淆矩阵的时候，如何计算相关指标？这里有两个个简单常用的方法。

1. 分别对各个混淆矩阵计算$(p_1,r_1)，.....,(p_n,r_n)$，然后对各个p和r取平均值，生成全局的精确率和召回率：
   $$mircoP=\sum _{i=1}^n{p}_i$$
   $$mircoR=\sum _{i=1}^n{r}_i$$
   $$marcoF1=\frac{2\ast microP\ast microR}{microP+microR}$$
2. 先计算，各个混淆矩阵中的TP,FP,TN,FN的的平均值
   $T{P}_{mean},F{P}_{mean},T{N}_{mean},F{N}_{mean}$,然后再根据这些来计算相关指标
   $$microP=\frac{T{P}_{mean}}{T{P}_{mean}+F{P}_{mean}}$$
   $$microR=\frac{T{P}_{mean}}{T{P}_{mean}+F{N}_{mean}}$$
   $$microF1=\frac{2\ast microP\ast microR}{microP+microP}$$

2、相关曲线

2.1 P-R曲线

我们将精确率和召回率的联合曲线称为：P-R曲线，如下图所示：

在上面的图示中，如果模型1的P-R曲线完全在模型2的P-R曲线之上，那么就可以认为模型1优于模型2。
BEP平衡点：
在该点上，精确率=召回率，一般认为该点的数值越高，模型越优。
F1值：
F1值是基于P和R的调和平均：
$$\frac{1}{F1}=\frac{1}{2}\ast (\frac{1}{P}+\frac{1}{R})$$
$$F1=\frac{2\ast P\ast R}{P+R}=\frac{2\ast TP}{样本总数+TP-TN}$$
同样，F1值越高，模型越优。
F1还有更一般的形式：
$$F_{\beta }=\frac{(1+{\beta }^2)\ast P\ast R}{({\beta }^2\ast P)+R}$$
其中β>0度量了召回率对于精确率的重要性。β>1时，召回率更重要，β<1时，精确率更重要。

2.2 ROC曲线与AUC曲线

我们现在假设TP,FN,FP,TN均为概率，则四者的关系为：
TP + FN = 1
FP + TN = 1
真正例率：$$TPR=\frac{TP}{TP+FN}$$
假正例率: $$FPR=\frac{FP}{TN+FP}$$
我们以假正例率为横轴，真正利率为纵轴，构建出一个相关的曲线，我们称之为ROC曲线。称ROC曲线包裹的面积为AUC。具体如下图所示：

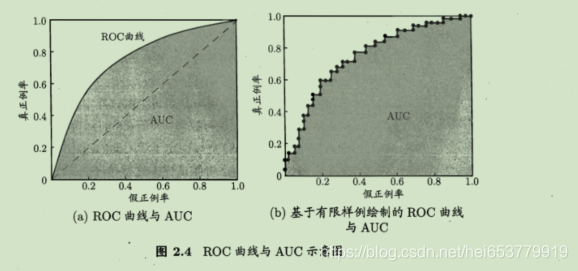
进行学习器比较的时候，与P-R曲线类似，当模型1的ROC曲线包裹了模型2的ROC曲线的时候，模型1更优。
另外一种比较是通过AUC的大小，AUC的估计计算公式为：
$$AUC=\frac{1}{2}\sum _{i=1}^{m=1}(x_{i+1}-x_i)\ast (y_i+y_{i+1})$$

2.3 代价敏感函数和代价曲线

在实际的任务中，分类错误所造成的代价可能是不同的，比如，将正例分类为负例的代价是1，而将负例分类为正例的代价为0.5。据此，我们可以构建出来一个代价矩阵。
其中，将第0类的样本分类为第1类的代价为$cos{t}_{01}$，将第1类样本分类为第0类的代价为$cos{t}_{10}$。在之前假设的FN，FP等指标中，计算的都是分类错误的次数，但是并没有指出错误的代价，也可以默认将分类错误的代价是相同的。在存在代价不同分类任务中，我们的目标不再是分类错的次数降低，而是期望分类错误造成的代价是最小的。
我们假设$D^{+}$为正例集，$D^{-}$为反例集。则存在代价敏感的错误率为：

在这种情况下，单纯的依赖ROC曲线是不能刻画总体代价的，我们采用“代价曲线”的度量方式，其中横轴采用：
$$P(+)cost=\frac{p\ast cos{t}_{01}}{p\ast cos{t}_{01}+(1-p)\ast cos{t}_{10}}$$
其中，p是样本为正例的概率，纵轴采用的是取值为[0,1]的归一化代价：
$$cos{t}_{norm}=\frac{FNR\ast p\ast cos{t}_{01}+FPR\ast (1-p)\ast cos{t}_{10}}{p\ast cos{t}_{01}+(1-p)\ast cos{t}_{10}}$$
其中，FRP是假正例率，FNR = 1 - TPR是假反例率。图示如下：

3 参考文献

周志华 《机器学习》