最近在实际工作中遇到一个解分线性方程的问题,于是学习了一下牛顿迭代算法,于是写了写个人的认识和体会。
首先直观的理解,如下图
是在f(x) 的零点附近取点(x0,f(x0)),然后以(x0,f(x0))做切线f(x0) + f'(x0)(x - x0) =0,求出切线的零点坐标x1 = x0 - f(x0)/f' (x0) ,依次进行下去x(n+1) = x(n) - f(x(n))/f'(x(n))------(1),可以发现点列(x0,x1,x2,x3...xn)越来越近我们要求的目标零点。
该原理可以用泰勒在x0出展开同样能得到相同的迭代关系。可以证明通过迭代,这个式子必然在f(x*) = 0时,收敛,详细的证明过程可以参考“http://wenku.baidu.com/link?url=Xwyi9EBNCpt3OB7bFdTO5uWYi1yTafB0tdPcP-eYWdR4gQOK-RHXFdA0qf_Zo7fnjWEhKkBgBXBMDUtHnjlIasTWuYjF1ARyUhrDsP_5WVe”。








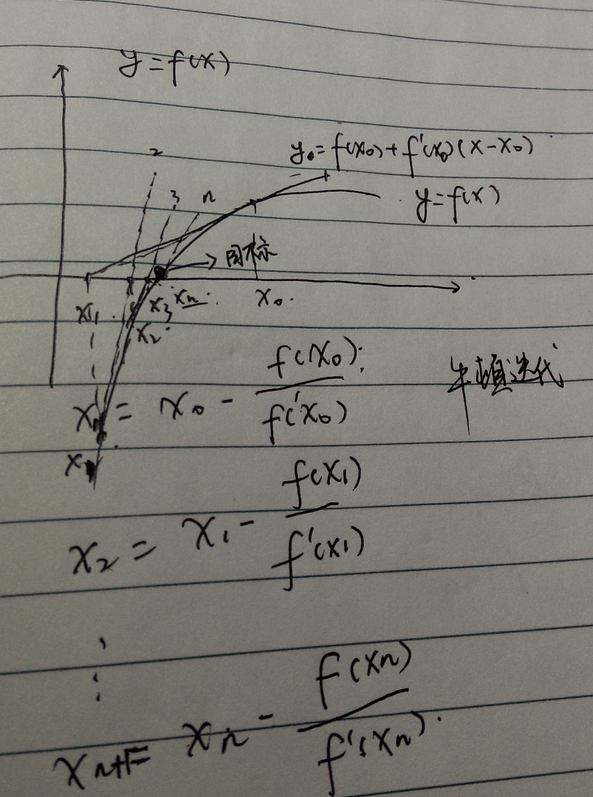














 7万+
7万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








