吉布斯现象

问题：为什么曲波阈值会带来噪声和伪影？

对信号处理一般可变换到变换域（小系数很有可能是高频，高频一般是噪声，但有可能也是信号），然后经过

1、阈值处理

2、频率截断（傅里叶变换），只保留自己希望的频率，具体得看信号的类型。

在频率截断时会出现吉布斯现象（在时域描述一个不连续的信号要求信号有无穷的频率成分。但实际情况是不可能采集到无穷的频率成分。信号采集系统只能采集一定频率范围内的信号，这将导致出现频率截断，频率截断会引起时域信号产生“振铃效应”（当使用少于合适数目的频率成分来描述信号时，就会产生振铃效应。），任何突然不连续或阶跃/转折信号总是会存在出现吉布斯现象）。

吉布斯现象 在工程应用时常用有限正弦项正弦波叠加逼近原周期信号。所用的谐波次数N的大小决定逼近原波形的程度，N增加，逼近的精度不断改善。但是由于对于具有不连续点的周期信号会发生一种现象：当选取的傅里叶级数的项数N增加时，合成的波形虽然更逼近原函数，但在不连续点附近会出现一个固定高度的过冲，N越大，过冲的最大值越靠近不连续点，但其峰值并不下降，而是大约等于原函数在不连续点处跳变值的9%，且在不连续点两侧呈现衰减振荡的形式。

讲到对信号进行FFT处理时，需要做截断，而截断又分为周期截断和非周期截断。FFT运算是对有限字长数据的傅里叶分析，其中会存在频谱泄露的现象，本来功率集中的频谱会出现能量外泄，污染其他频带的信号，造成一定的性能损失，甚至整体功能失效。
FFT是DFT的一种快速计算方法，而由信号与系统理论可知，有限长信号的DFT，是假设该信号为一个周期信号的片段（周期）来进行计算的，也就是说将有限长信号进行周期拓展，然后再进行周期信号的傅里叶谱计算。
假设原始信号是单频正弦波，如果截断的时间长度刚好是信号周期的整数倍，那么，截断后的每帧数据仍是周期信号，可重构得到原始的周期信号，如图3所示。此时，信号的频谱为单一频率的线状谱，如图4所示。

                                                              图三：周期截断

倘若信号截断的时间长度不为原始正弦信号周期的整数倍，那么，截断后的信号则不为周期信号。对同一个正弦信号进行非周期截断，如图5所示，截断后的信号起始时刻和结束时刻的幅值明显不等，将这个信号再进行重构，在连接处信号的幅值不连续，出现阶跃，如图5中黑色圆圈区域所示。对这个信号进行FFT分析，得到的频谱如图6所示，不再是正确的线状谱了，而是出现了明显的频率拖尾效应，频率成分分布在整个频带上了。

 

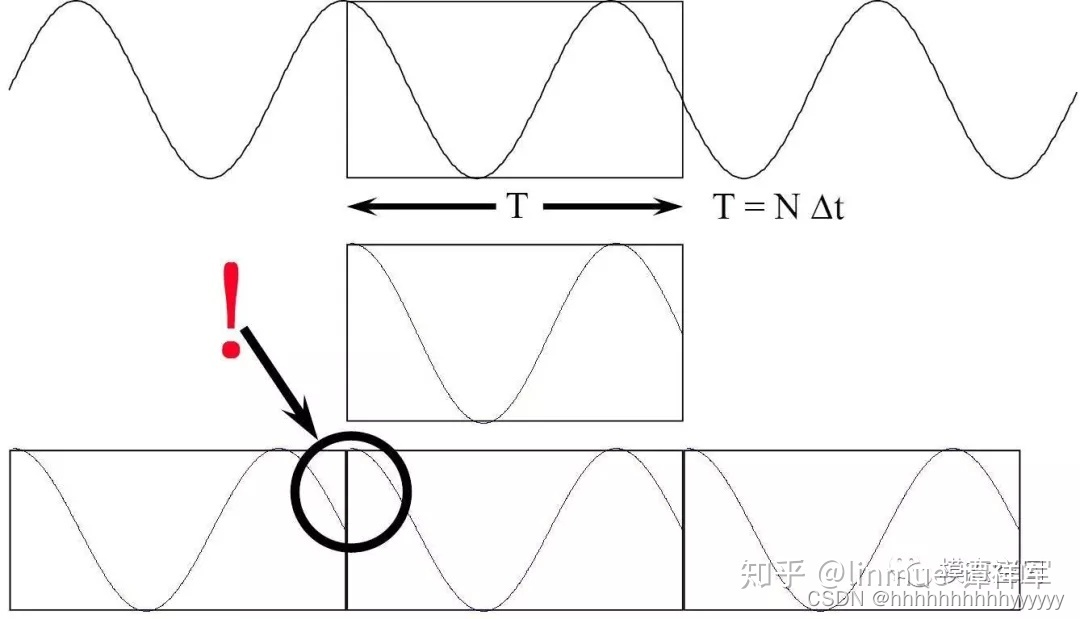
                                                                     图五 非周期截断

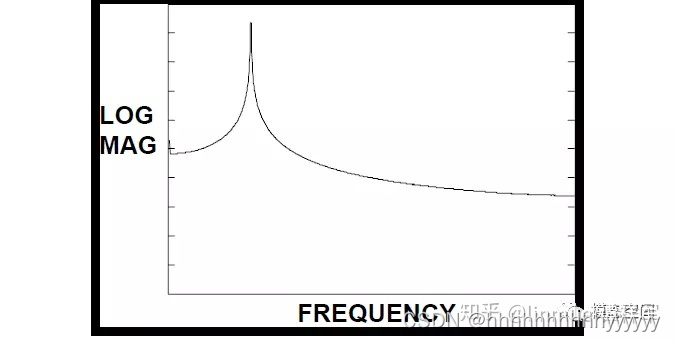
                                                      图6 非周期截断导致频谱拖尾

对于具有不连续点（跳变点）的波形，所取级数项数越多，近似波形的均方误差虽可减少，但在跳变点处的峰起值不能减少，此峰起值随项数增多向跳变点靠近。

     

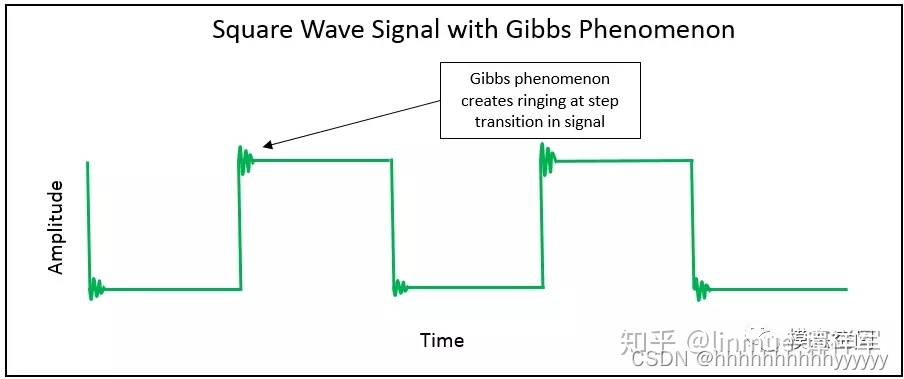
                                                     图9 方波中的吉布斯现象

代码：
%（3）
t=-pi:0.001:pi;
N=input('N=');
for j=1: N
f = zeros(size(t));
for i=1:j
f = f + (sin(i*t))/i;
end
fmax(j) = (max(f)-pi/2)/pi;
end
figure(1); plot(t, f, 'r');
hold on;
y=-pi/2*sawtooth(t);
plot(t,y);axis([-4 4 -2 2]) ;
title(['N=', num2str(N)]);
figure(2); plot(fmax) ;
legend('(f_{n}-f)/f(max)');
axis([0 200 -0.2 0.15]);
title('吉布斯现象');
%（4）
t=-pi:0.001:pi;
N=input('N=');
F0= zeros(size(t));
for j=1:N
f = zeros(size(t));
for i=1:j
f = f + (sin(i*t))/i;
F0=F0+(sin(i*t))/i;
end
end
F=F0/n;
y=-pi/2*sawtooth(t);
plot(t, f);hold on;
plot(t,y);
plot(t,F) ;title(['n=', num2str(n)]);
legend('f_{N}(t)','sawtooth','F_{N}(t)');