线性回归（2）缩减系数理解

最新推荐文章于 2022-04-22 16:14:32 发布

hhy518518

最新推荐文章于 2022-04-22 16:14:32 发布

阅读量2k

点赞数

分类专栏：数据科学机器学习文章标签：读书笔记机器学习 python 数据 algorithm

本文链接：https://blog.csdn.net/hhy518518/article/details/53573843

版权

本文探讨了在数据特征超过样本点时的线性回归问题，介绍了岭回归的概念，解释了其如何通过调整λ来优化系数，并对比了与线性回归的关系。同时提到了LASSO回归，指出其与岭回归的不同约束形式，并讨论了在λ取值小时对数据的理解。此外，文章还涉及前向逐步回归算法和权衡偏差与方差的重要性，并通过预测乐高玩具价格的实例进行了分析。

摘要由CSDN通过智能技术生成

摘要：

当我们的数据特征比样本点还多怎么办，是否能够预测呢答案是否定。

岭回归

那么如何解决这个问题呢？科学家们引入了岭回归这个概念，岭回归其实就是如下：

与前面的算法相比。这里通过预测误差的最小化得到系数首先抽取一部分用于训练I的系数，剩下的再来训练W

def ridgeRegres(xMat,yMat,lam=0.2):
    xTx = xMat.T*xMat
    denom = xTx +eye(shape(xMat)[1])*lam
    if linalg.det(denom)==0.0:
        print "this matrix is singular"
        return
    ws = denom.I*(xMat.T*yMat)
    return ws

def ridgeTest(xArr,yArr):
    xMat = mat(xArr);yMat = mat(yArr).T
    yMean = mean(yMat,0)
    xMeans = mean(xMat,0)
    xVar = var(xMat,0)
    xMat = (xMat-xMeans)/xVar
    numTestPtS = 30
    wMat = zeros((numTestPtS,shape(xMat)[1]))
    for i in range(numTestPtS):#lamda is different
        ws = ridgeRegres(xMat,yMat,exp(i-10))
        wMat[i,:] = ws.T
    return wMat

而代码主要改变的是Lambda 用30个不同的来进行实验，获得一个权重矩阵，每一行代表不同的Lambda所对应的权重

reload(regression)
abX,abY = regression.loadDataSet('abalone.txt')
ridgeWeights = regression.ridgeTest(abX,abY)

import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.plot(ridgeWeights)
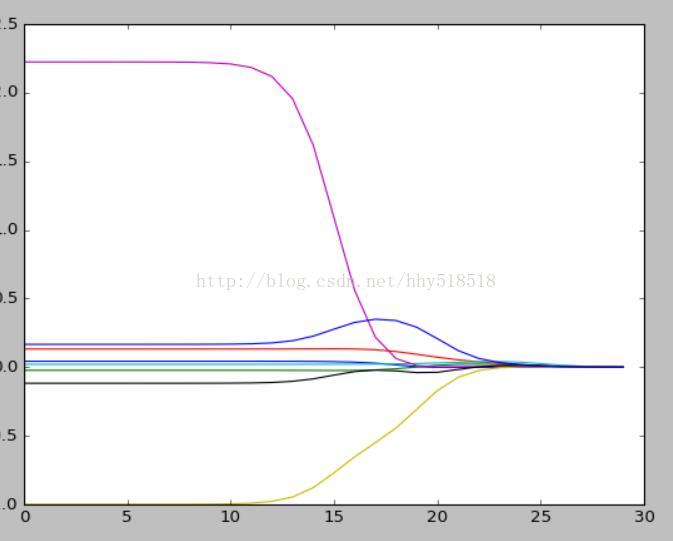
plt.show()

我们绘制出Lambda的图形