小波变换 python MITBIH数据库基线漂移去噪

最新推荐文章于 2025-05-15 15:14:39 发布

原创最新推荐文章于 2025-05-15 15:14:39 发布 · 4.9k 阅读

53 ·

CC 4.0 BY-SA版权

文章标签：

#python #深度学习 #机器学习

心电信号分析专栏收录该内容

4 篇文章

订阅专栏

本文介绍如何利用小波变换处理心电信号中的基线噪声。通过选用合适的分解层数与小波基(sym8)，有效提取并减弱了低频噪声。文章提供了Python代码实例，并分析了时频域的变化。

部署运行你感兴趣的模型镜像

文章目录

基线噪声

对于心电信号，，基线信号存在于脉搏信号中。对于基线，一般频率小于0.5HZ,不存在与心电信号频谱重叠的区域。因此采用基于sym8小波函数对信号进行分解，提取0~0.1HZ内的基线信号。

小波基选择

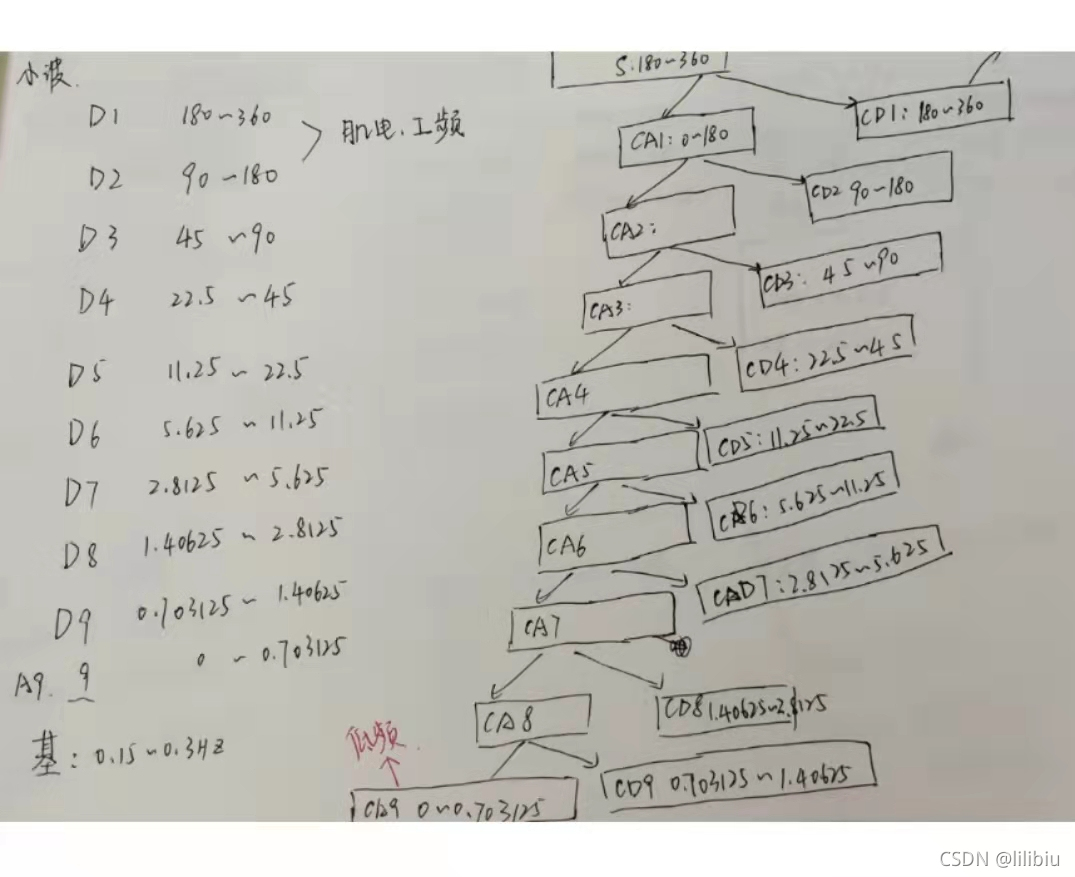
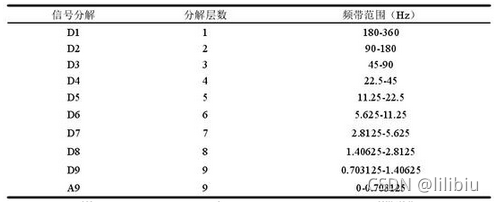
在这里插入图片描述

分解示意图

在这里插入图片描述

如上图所示，9层分解之后，得到的CA9的频率范围是0~0.703125HZ,
如果只分解8层，则会CD8频率范围1.40625~2.8125,因此选择9层分解。

对于MIT-BIH数据库（采样率360hz）的数据进行小波9层分解，每一层分解如图所示。
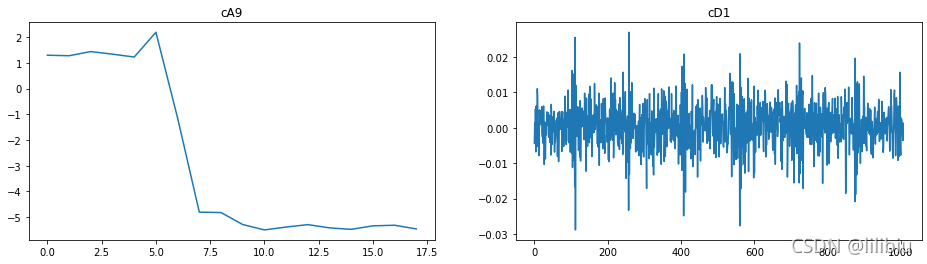
在这里插入图片描述

代码实现与时频域分析

cA9, cD9, cD8, cD7, cD6, cD5, cD4, cD3, cD2, cD1 = coeffs #数字越小频率越大

注意代数与频率的对应关系，CD1代表的是高频，CA9则是本次分解的最低频。

在这里插入图片描述
小波变换前后的时频域图像如下图所示：

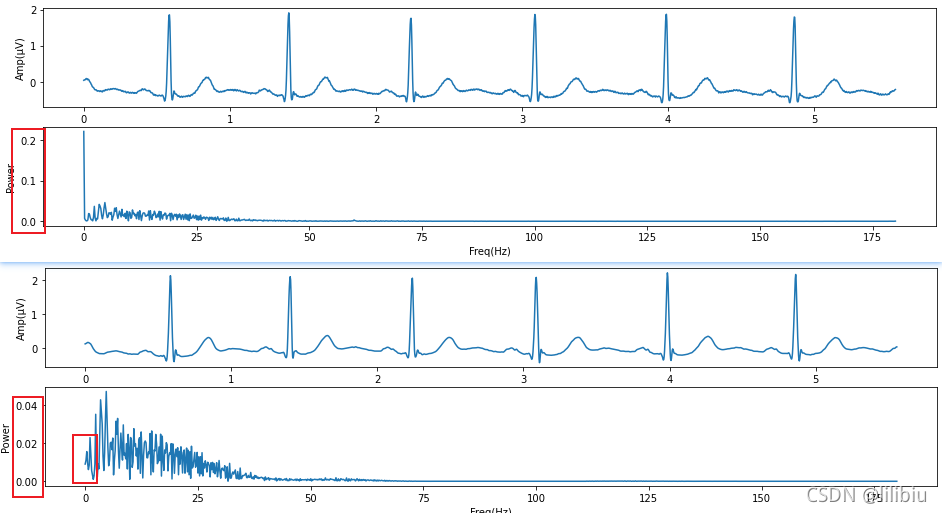
在这里插入图片描述
可以看到小波变换之后，0HZ周围的噪声已经减弱。

代码也很简单，本网站有很多，需要的也可以留言邮箱。

def WT(data,wavelet,level):
    #小波变换之后
    Data = data.flatten()
    coeffs = pywt.wavedec(data = Data, wavelet = wavelet, level = level)   
    # print(len(coeffs))
    cA9, cD9, cD8, cD7, cD6, cD5, cD4, cD3, cD2, cD1 = coeffs #数字越小频率越大
    plt.figure(figsize=(16,4))
    plt.subplot(1,2,1)
    plt.plot(cA9)
    plt.title('cA9')
    plt.subplot(1,2,2)
    plt.plot(cD1)
    plt.title('cD1')
    # 将高频信号cD1、cD2,低频信号CA9置零
    cD1.fill(0)
    cD2.fill(0)
    cD9.fill(0)
    cA9.fill(0)
    #180~360, 90~180,0.703125~1.40625,0~0.703125 均置为0
    rdata = pywt.waverec(coeffs, wavelet='sym8')
    return rdata

如果需要软阈值滤波：

threshold = (np.median(np.abs(cD1)) / 0.6745) * (np.sqrt(2 * np.log(len(cD1))))
# 将高频信号cD1、cD2置零
cD1.fill(0)
cD2.fill(0)
# 将其他中低频信号按软阈值公式滤波
for i in range(1, len(coeffs) - 2):
    coeffs[i] = pywt.threshold(coeffs[i], threshold)