卷积神经网络的深入理解-最优化方法(梯度下降篇)(持续更新)
说起最优化方法,我们首先要知道优化目标是什么,优化目标有凸函数和非凸函数两种,而我们要尽可能的寻找相对小的值

凸函数全局最小值=局部最小值

非凸函数包含许多局部最小值
那么更新方式有几种呢,就如我们下山一样,取决于我们所走的方向和每一步所走的距离,即学习率和更新方向。
下面是方法列表(这里主要是一阶的优化方法)
| 基于学习率的选择 | 基于更新方向 |
|---|---|
| Adagrad法 | 随机梯度下降SGD法 |
| Adadelta与Rmsprop法 | momentum动量法 |
| Adam,AdaMax,Nadam法 | Nesterov accelerated gradient法 |
| AMSgrad法 | |
| Adafactor法 | |
| Adabound法 |
这里选择常见的几种进行介绍(之后会对遇到的进行补充)
一、更新方向
1、随机梯度下降SGD
随机体现在,在计算梯度下降时,从下降最快的方向随机选一个数据进行计算。其参数更新如下:
θ
n
+
1
=
θ
n
−
η
Δ
θ
J
(
θ
)
\theta_{n+1} =\theta_{n}- \eta \Delta_{\theta}J(\theta)
θn+1=θn−ηΔθJ(θ)
现参数 = 原参数减去学习率 X 其梯度
| 优点 | 缺点 |
|---|---|
| 简单 | 不稳定,对学习率敏感,迭代慢 |
2、动量法
动量法是对SGD算法的改进
加速SGD,特别是处理高曲率小、但一致的梯度;累积了之前梯度指数级衰减的移动平均,并继续沿该方向移动。
m
n
+
1
=
β
m
n
+
η
▽
θ
J
(
θ
)
,
θ
n
+
1
=
θ
n
−
m
n
−
1
m_{n+1}=\beta m_{n}+\eta \triangledown_{\theta}J(\theta), \theta_{n+1}=\theta{n}-m_{n-1}
mn+1=βmn+η▽θJ(θ),θn+1=θn−mn−1
相较于SGD算法,动量法多了一部分
β
m
n
\beta m_{n}
βmn,
β
\beta
β默认是0.9,如下图所示
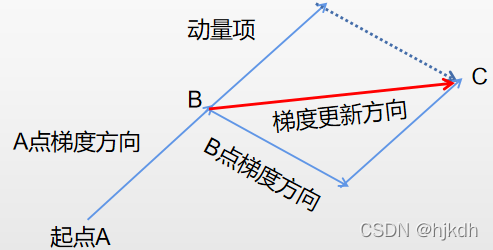
B点的梯度方向加上动量项的梯度方向就是B点的梯度更新方向,更新后到达C点。这里在网上找了一张图片,黑色是SGD法,红色是动量法。
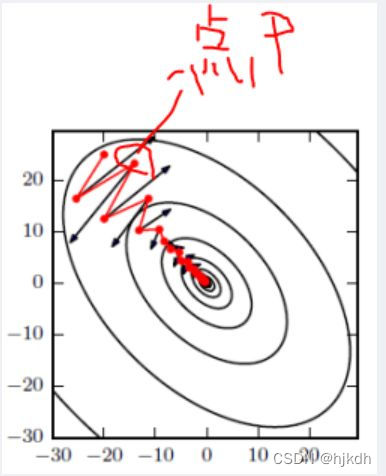
3、Nesterov accelerated gradient法(NAG法)
这种方法在标准动量法的基础上加了一个矫正因子,使得梯度下降更快,更加智能。公式和图像如下(不过为何会加快不太理解,知道的朋友可以告诉我一下):
m
n
+
1
=
β
m
n
+
η
▽
θ
J
(
θ
−
β
m
n
)
,
θ
n
+
1
=
θ
n
−
m
n
−
1
m_{n+1}=\beta m_{n}+\eta \triangledown_{\theta}J(\theta-\beta m_{n}), \theta_{n+1}=\theta{n}-m_{n-1}
mn+1=βmn+η▽θJ(θ−βmn),θn+1=θn−mn−1

二、更新学习率
1、Adagrad法
自适应地为各个维度的参数分配不同的学习率
G
t
=
G
t
−
1
+
g
t
2
G_{t}=G_{t-1}+{g_{t}}^{2}
Gt=Gt−1+gt2
Δ
θ
t
=
−
η
G
t
+
ε
∗
g
t
\Delta \theta_{t}=-\frac{\eta }{\sqrt{G_{t}+\varepsilon }}*g_{t}
Δθt=−Gt+εη∗gt
g
t
g_{t}
gt是当前的梯度,
η
η
η是初始学习率,
G
t
G_{t}
Gt是梯度平方累积值,
ε
ε
ε是一个比较小的数。
| 优点 | 缺点 |
|---|---|
| gt较小的时候,能够放大梯度,较大的时候,能够约束梯度 | 后期学习率非常小,需要设置一个合适的全局初始学习率 |
三、更新学习率+更新方向
1、Adam法
Adam法对梯度的一阶和二阶都进行了估计和偏差修正,使用梯度的一阶矩估计和二阶矩估计来动态调整每个参数的学习率。
公式如下:

| 优点 | 缺点 |
|---|---|
| 对学习率没有那么敏感,学习步长有一个确定的范围,参数更新比较稳 | 学习率在训练的后期仍可能不稳定导致无法收敛到足够好的值,泛化能力较差。 |
下面是一些总结
| 采用改进的SGD算法的优点 | 采用改进SGD算法的缺点 |
|---|---|
| 减少了调参工作量 | 不稳定,收敛效果不如精细调参的SGD算法 |
也可以采用二阶方法进行优化,上面采用的都是一阶方法,当然采用二阶方法也有利弊。
| 采用二阶算法的优点 | 采用二阶算法的缺点 |
|---|---|
| 二阶的方法因为使用了导数的二阶信息,因此其优化方向更加准确,速度也更快 | 计算量大,一阶方法一次迭代更新复杂度为O(N),二阶方法就是O(N*N) |
























 4121
4121

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








