虎书学习笔记-数字信号处理（一）

一、什么是数字信号处理？

数字信号处理分为两个过程：

1）采样（sampling）：数码设备通过模拟-数码转换器通过捕获特定形式的物理信息，将其转换为数字存储到设备中，作为采样数据。
2）重建（reconstruction）：数码设备将存储的采样数据通过数码-模拟转换器将数字转换为捕获的物理信息，以物理信息原本的形式“播放”。

二、一种简单的数字信号处理过程

0）数字信号处理在生活中的应用：在生活中我们使用到的许多物品都有数字信号处理的过程，像数码相机拍摄照片时、麦克风捕捉我们的说话声时就进行了采样，耳机播放音乐时、电视机或手机等电子设备在屏幕上显示图案时就进行了重建。
1）这一节中，我们介绍一个简单的数字信号处理模型：数字音频

模型示意图如下所示：

在麦克风录音的时候，记录的声音是在空气中以压力波存在着的，而麦克风通过低通滤波器将其转换为了随时间变化的电压，这样的物理信息就存储进了麦克风。而当要播放记录的声音时，音响就同样会以变化的电压通过低通滤波器来形成空气中的压力波。而接下来我们要重点介绍物理信息和数字信息之间是如何转换的。

在录音的过程中，就进行了采样，此时麦克风记录的物理信息就会通过A/D转换器（analog-to-digital converter）转换为整形数据流存储在像光盘等便携式硬件中。

在播放音频时，就进行了重建，这时存储的数据就以合适的频率读取，通过D/A转换器（digital-to-analog converter）转换为物理信息传递给音响等播放声音的硬件。

三、数字信号处理中遇到的问题

在上一节的数字音频模型中，如果我们录音的采样频率低于被录声音的频率，那么在重建声音的过程中就会出现一些不自然的声音，或者说不是我们原本录的声音。这一现象被称为失真。

同样的事情在计算机图形学领域中也有发生，像对图片进行采样时低于特定频率，在重构图片时也会出现重构的图片会有撕裂的区域。这一现象称为畸变。

这样类似的现象就引出了这样的问题

• 多大的采样频率才能保证好的效果？
• 怎样的滤波器（filter）对于采样和重建是合适的？
• 需要多大的平滑程度才能避免信号的错误识别（aliasing）？

为了解决这样的难题，我们首先要补充一些理论知识。

四、理论知识：卷积（一）

卷积是将两个函数结合形成一个新函数的操作，在虎书中使用*表示卷积的运算符，例如函数f对g的卷积可以表示为
$$f\ast g$$

卷积适用范围也很大，不仅可以适用于连续函数，也能适用于离散的数组，不仅可以适用于一元函数，还可以适用于多元函数，本节主要介绍一元函数的情况。

1）移动平均值

在一元函数中，为了得到函数任意一点的平滑变化的值，我们通过可以计算一个半径为r的邻域内函数值的平均值，其中r是控制平滑程度的参数。比如平滑化一个连续函数g(x)，我们就可以通过对g积分这样操作：
$$h(x)=\frac{1}{2r}{\int }_{x-r}^{x+r}g(t)dt$$
类似地，对于一组离散数据构成的数组a[i]我们就可以对其求和：
$$c[i]=\frac{1}{2r+1}\sum _{j=i-r}^{i+r}a[j]$$
为什么要提这个呢，因为虎书是这样说的

This idea of a moving average is the essence of convolution; the only differ-
ence is that in convolution the moving average is a weighted average.

2）离散卷积

对于两个数组a[i]和b[i]，我们定义数组a对b在某一位置i处的卷积为：
$$(a\ast b)[i]=\sum _{j}a[j]b[i-j]$$
其中值b[i-j]为位置j的权重，也就是距离位置i长度为i-j处的值。如图所示是一个计算的例子：

其中$$b=\frac{1}{16}[...,0,1,4,6,4,1,0,...]$$也就是说，b[0]=6/16，a[1]=a[-1]=4/16等等。

在图形学中，两个函数中的一个通常在有限个自变量区间是非零的，如果我们假设b满足这样的条件，这时有对于参数r满足当|k|大于r有b[k]=0，这样我们就可以将以上卷积定义为：
$$(a\ast b)[i]=\sum _{j=i-r}^{i+r}a[j]b[i-j]$$

i）虎书中的解释说明（便于理解卷积过程）
关于箱式过滤器（box filter）的介绍和一个简单的卷积计算例子

ii）性质
性质一：卷积运算满足乘法运算的规律
结合律：(a * b)[i]=(b * a)[i]
交换律：(a* (b * c))[i]=((a * b) * c)[i]
分配律：(a * (b + c))[i]=(a * b + a * c)[i]

简单证明结合律：
对于公式$$(a\ast b)[i]=\sum _{j}a[j]b[i-j]$$
如果我们令j=i-k，那么公式可以写成
$$\begin{gathered} (a\ast b)[i]=\sum _{k}a[i-k]b[i-(i-k)] \\ =\sum _{k}b[k]a[i-k] \end{gathered}$$
这就证明了结合律。

性质二：滤波器为恒量滤波器时，函数对其的卷积等于其本身

恒量滤波器，是一个半径为零，或像d[i]=…,0,0,1,0,0,…这样的滤波器。

数组a[i]对d[i]的卷积则为
$$\begin{gathered} (a\ast d)[i]=\sum _{j=i}^{j=i}a[j]d[i-j] \\ =a[i] \end{gathered}$$

3）连续卷积

对于两个连续函数f和g，二者的卷积为：
$$(f\ast g)(x)={\int }_{-\infty }^{+\infty }f(t)g(x-t)dt$$
可以理解为随着参数x变化，函数f(t)g(x-t)从负无穷到正无穷区间内的积分值。图示如下：

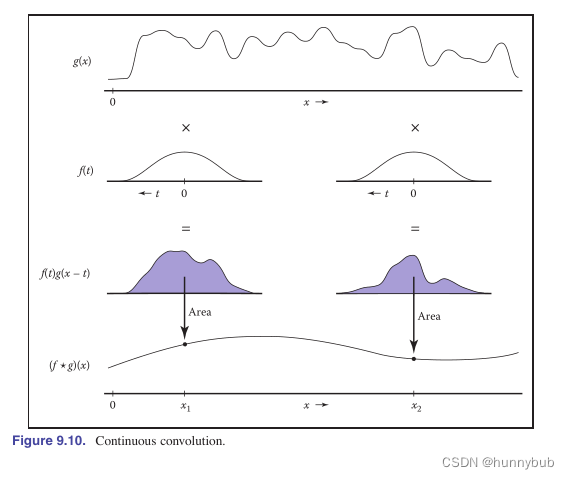
一个简单的计算例子：

注意这里separation应理解为“两个box之间的距离”

4）离散-连续卷积

当我们要计算一个离散数组a[i]和连续函数f(x)的卷积时，一种计算方式是通过对f(x)采样得到离散的数组f[i]进行计算，另一种方式是对数组a[i]进行重建，使其成为连续函数a(x)。

在将离散的数组a[i]与连续函数f(x)进行卷积时，写为以下形式
$$(a\ast f)(x)=\sum _{i}a[i]f(x-i)$$
示意图如下：

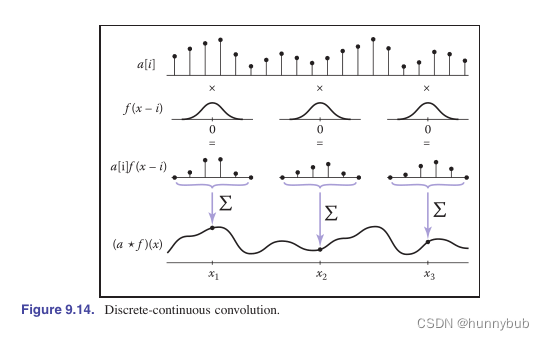
当我们确定了滤波器的半径r时，卷积表达式可以写为
$$(a\ast f)(x)=\sum _{i=\lceil x-r\rceil }^{\lfloor x+r\rfloor }a[i]f(x-i)$$
这里需要注意的是如果点正好落在距离点x为r的位置，将不进行求和。