9.7 python模拟常用分布

本章用Python统计模拟的方法，介绍四种常用的统计分布，包括离散分布：二项分布和泊松分布，以及连续分布：指数分布和正态分布，最后查看人群的身高和体重数据所符合的分布。
首先导入python相关模块：

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib inline
%config InlineBackend.figure_format = 'retina'

随机数

计算机发明后，便产生了一种全新的解决问题的方式：使用计算机对现实世界进行统计模拟。该方法又称为“蒙特卡洛方法（Monte Carlo method）”，起源于二战时美国研制原子弹的曼哈顿计划，它的发明人中就有大名鼎鼎的冯·诺依曼。蒙特卡洛方法的名字来源也颇为有趣，相传另一位发明者乌拉姆的叔叔经常在摩洛哥的蒙特卡洛赌场输钱，赌博是一场概率的游戏，故而以概率为基础的统计模拟方法就以这一赌城命名了。
使用统计模拟，首先要产生随机数，在Python中，numpy.random 模块提供了丰富的随机数生成函数。比如生成0到1之间的任意随机数：

np.random.random(size=5)  # size表示生成随机数的个数

运行结果

array([ 0.32392203,  0.3373342 ,  0.51677112,  0.28451491,  0.07627541])

又比如生成一定范围内的随机整数：

np.random.randint(1, 10, size=5)  # 生成5个1到9之间的随机整数

运行结果

array([5, 6, 9, 1, 7])

计算机生成的随机数其实是伪随机数，是由一定的方法计算出来的，因此我们可以按下面方法指定随机数生成的种子，这样的好处是以后重复计算时，能保证得到相同的模拟结果。

np.random.seed(123)

在NumPy中，不仅可以生成上述简单的随机数，还可以按照一定的统计分布生成相应的随机数。这里列举了二项分布、泊松分布、指数分布和正态分布各自对应的随机数生成函数，接下来我们分别研究这四种类型的统计分布。

• np.random.binomial()
• np.random.poisson()
• np.random.exponential()
• np.random.normal()

二项分布

二项分布（伯努利分布）是n个独立的是/非试验中成功的次数的概率分布，其中每次试验的成功概率为p。这是一个离散分布，所以使用概率质量函数（PMF）来表示k次成功的概率：

$$f(k;n,p)= \big( ^k_n \big)p^k(1-p)^{n-k}$$
最常见的二项分布就是投硬币问题了，投n次硬币，正面朝上次数就满足该分布。下面我们使用计算机模拟的方法，产生10000个符合（n，p）的二项分布随机数，相当于进行10000次实验，每次实验投掷了n枚硬币，正面朝上的硬币数就是所产生的随机数。同时使用直方图函数绘制出二项分布的PMF图。

def plot_binomial(n,p):
    '''绘制二项分布的概率质量函数'''
    sample = np.random.binomial(n,p,size=10000)  # 产生10000个符合二项分布的随机数
    bins = np.arange(n+2) 
    plt.hist(sample, bins=bins, align='left', normed=True, rwidth=0.1)  # 绘制直方图
    #设置标题和坐标
    plt.title('Binomial PMF with n={}, p={}'.format(n,p))  
    plt.xlabel('number of successes')
    plt.ylabel('probability')

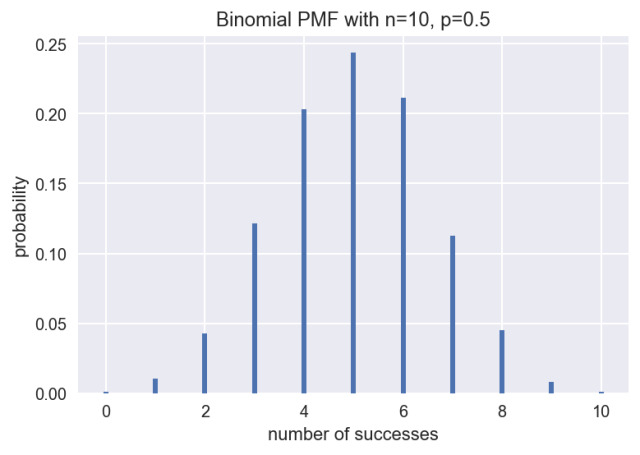
plot_binomial(10, 0.5)

投10枚硬币，如果正面或反面朝上的概率相同，即p=0.5， 那么出现正面次数的分布符合上图所示的二项分布。该分布左右对称，最有可能的情况是正面出现5次。
但如果这是一枚作假的硬币呢？比如正面朝上的概率p=0.2，或者是p=0.8，又会怎样呢？我们依然可以做出该情况下的PMF图。

fig = plt.figure(figsize=(12,4.5)) #设置画布大小
p1 = fig.add_subplot(121)  # 添加第一个子图
plot_binomial(10, 0.2)
p2 = fig.add_subplot(122)  # 添加第二个子图
plot_binomial(10, 0.8)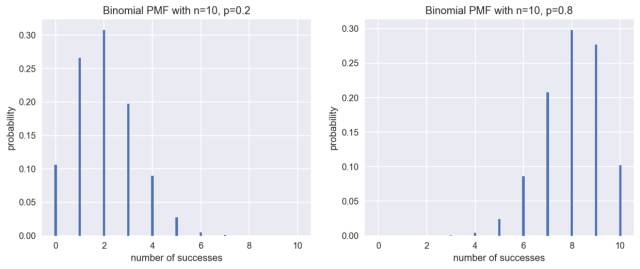

这时的分布不再对称了，正如我们所料，当概率p=0.2时，正面最有可能出现2次；而当p=0.8时，正面最有可能出现8次。

泊松分布

泊松分布用于描述单位时间内随机事件发生次数的概率分布，它也是离散分布，其概率质量函数PMF为：

$$f(k;\lambda)=\frac{e^{-\lambda}\lambda^k}{k!}$$
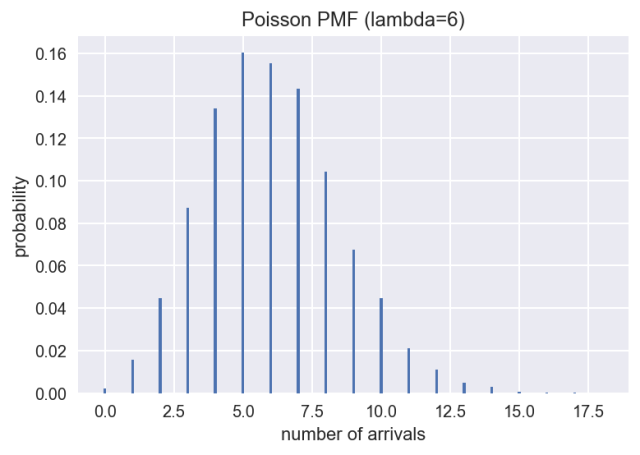
比如你在等公交车，假设这些公交车的到来是独立且随机的（当然这不是现实），前后车之间没有关系，那么在1小时中到来的公交车数量就符合泊松分布。同样使用统计模拟的方法绘制该泊松分布，这里假设每小时平均来6辆车（即上述公式中lambda=6）。

lamb = 6
sample = np.random.poisson(lamb, size=10000)  # 生成10000个符合泊松分布的随机数
bins = np.arange(20)
plt.hist(sample, bins=bins, align='left', rwidth=0.1, normed=True) # 绘制直方图# 设置标题和坐标轴
plt.title('Poisson PMF (lambda=6)')
plt.xlabel('number of arrivals')
plt.ylabel('probability')
plt.show()

指数分布

指数分布用以描述独立随机事件发生的时间间隔，这是一个连续分布，所以用质量密度函数表示：

$$f(x;\lambda)=\lambda e^{-\lambda x}(x≥0)$$
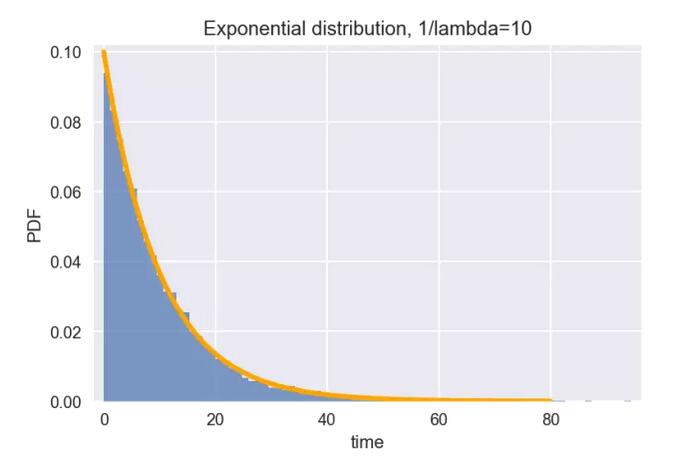
比如上面等公交车的例子，两辆车到来的时间间隔，就符合指数分布。假设平均间隔为10分钟（即1/lambda=10)，那么从上次发车开始，你等车的时间就满足下图所示的指数分布。

tau = 10
sample = np.random.exponential(tau, size=10000)  # 产生10000个满足指数分布的随机数
plt.hist(sample, bins=80, alpha=0.7, normed=True) #绘制直方图
plt.margins(0.02) 

# 根据公式绘制指数分布的概率密度函数
lam = 1 / tau
x = np.arange(0,80,0.1)
y = lam * np.exp(- lam * x)
plt.plot(x,y,color='orange', lw=3)#设置标题和坐标轴
plt.title('Exponential distribution, 1/lambda=10')
plt.xlabel('time')
plt.ylabel('PDF')
plt.show()

正态分布

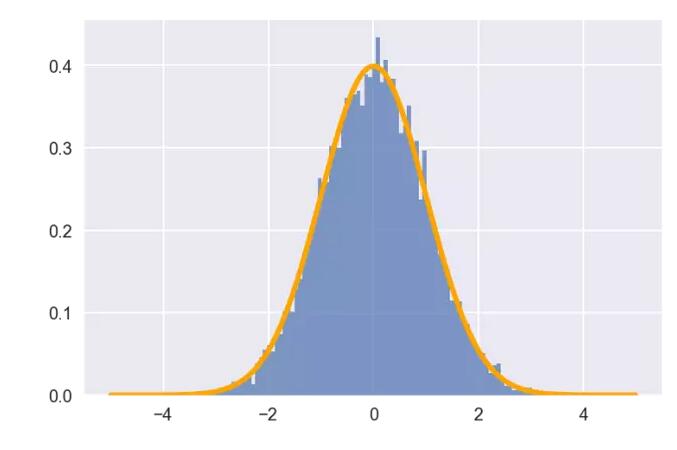
正态分布是一种很常用的统计分布，可以描述现实世界的诸多事物，具备非常漂亮的性质，其概率密度函数为

$$f(x;\mu,\sigma)=\frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{(x-\mu)^2}{2e^2}}$$
以下绘制了均值为0，标准差为1的正态分布的概率密度曲线，其形状好似一口倒扣的钟，因此也称钟形曲线

def norm_pdf(x,mu,sigma):
    '''正态分布概率密度函数'''
    pdf = np.exp(-((x - mu)**2) / (2* sigma**2)) / (sigma * np.sqrt(2*np.pi))    return pdf

mu = 0    # 均值为0
sigma = 1 # 标准差为1
# 用统计模拟绘制正态分布的直方图
sample = np.random.normal(mu, sigma, size=10000)
plt. hist(sample, bins=100, alpha=0.7, normed=True)# 根据正态分布的公式绘制PDF曲线
x = np.arange(-5, 5, 0.01)
y = norm_pdf(x, mu, sigma)
plt.plot(x,y, color='orange', lw=3)
plt.show()