人工智能之数学基础：随机向量的期望和随机向量函数的期望

本文重点

在前面的课程中，我们介绍了随机变量的数学期望，本文我们将学习随机向量的数学期望。随机向量的数学期望和随机变量的数学期望的计算方式大致是相同的。

随机向量的数学期望的直观理解

随机向量是一个向量，随机向量的期望也是一个向量。

随机向量的每一个元素都是一个随机变量，只需要计算出每一个随机变量的期望，然后组成向量就可以得到随机向量的期望了。

公式

现在有一个随机向量X=[X1,X2],对于每一个随机变量X1、X2分别计算期望E[X1]、E[X2]，就可以得到随机向量X的期望了E[X]=[E[X1],E[X2]]

对于离散型随机向量，分量Xi的数学期望为：

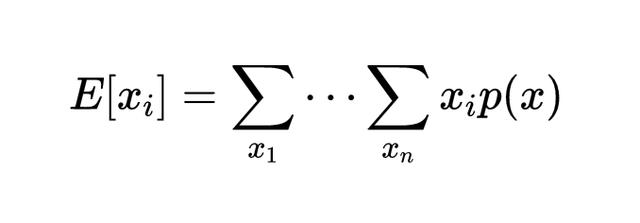
针对于离散型进行举例，现在随机向量x的联合概率质量函数如下所示：

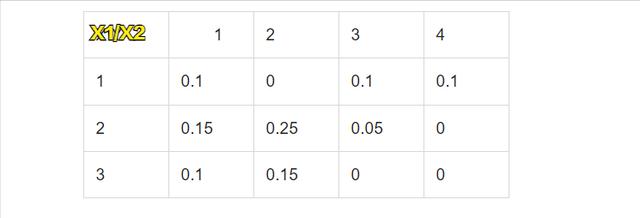
E[X1]=1*0.1+1*0+1*0.1+1*0.1+2*0.15+2*0.25+2*0.05+2*0+3*0.1+3*0.15+3*0+3*0=0.1+0.1+0.1+0.3+0