如何通俗易懂地理解皮尔逊相关系数？

要理解 Pearson 相关系数，首先要理解协方差（Covariance）。协方差表示两个变量 X，Y 间相互关系的数字特征，其计算公式为：

$COV(X,Y)=\frac{1}{n-1}{\sum }_1^n(X_i-\overline{X})(Y_i-\overline{Y})$

当 Y = X 时，即与方差相同。当变量 X，Y 的变化趋势一致时，如果某个 $X_i$ 大于 $\overline{X}$，相应的 $Y_i$ 也大于 $\overline{Y}$；如果某个 $X_i$ 小于 $\overline{X}$，相应的 $Y_i$ 也小于 $\overline{Y}$，那么 $COV(X,Y)$ 就是正值，当变量 X，Y 的变化趋势相反时，那么 $COV(X,Y)$ 就是负值。

Pearson 相关系数公式如下：

$COR(X,Y)=\frac{{\sum }_1^n(X_i-\overline{X})(Y_i-\overline{Y})}{\sqrt{{\sum }_1^n(X_i-\overline{X}{)}^2{\sum }_1^n(Y_i-\overline{Y}{)}^2}}$

由公式可知，Pearson 相关系数是用协方差除以两个变量的标准差得到的，虽然协方差能反映两个随机变量的相关程度（协方差大于0的时候表示两者正相关，小于0的时候表示两者负相关），但其数值上受量纲的影响很大，不能简单地从协方差的数值大小给出变量相关程度的判断。为了消除这种量纲的影响，于是就有了相关系数的概念。

当两个变量的方差都不为零时，相关系数才有意义，相关系数的取值范围为[-1,1]。《数据挖掘导论》中给了一个很形象的图来说明相关度大小与相关系数之间的联系：

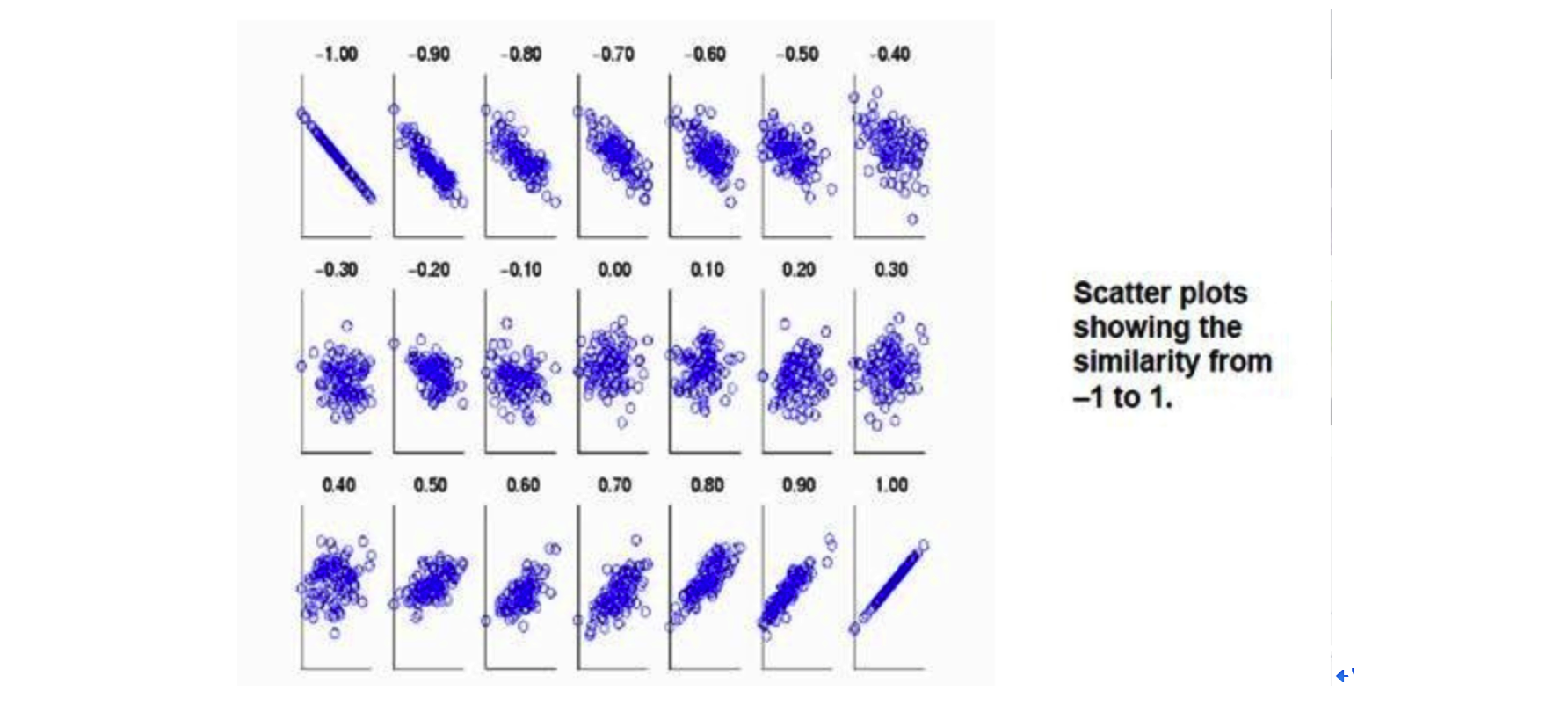
由上图可以总结，当相关系数为1时，成为完全正相关；当相关系数为-1时，成为完全负相关；相关系数的绝对值越大，相关性越强；相关系数越接近于0，相关度越弱。

关于皮尔逊相关系数的编程计算，MATLAB 中提供了现有的函数：

cor = corr(Matrix,'type','Pearson')

Matrix 参数即为需要计算的矩阵。