leetcode 572. Subtree of Another Tree

Given two non-empty binary trees s and t, check whether tree t has exactly the same structure and node values with a subtree of s. A subtree of s is a tree consists of a node in s and all of this node's descendants. The tree s could also be considered as a subtree of itself.

Example 1:
Given tree s:

     3
    / \
   4   5
  / \
 1   2

Given tree t:

   4 
  / \
 1   2

Return  true, because t has the same structure and node values with a subtree of s.

Example 2:
Given tree s:

     3
    / \
   4   5
  / \
 1   2
    /
   0

Given tree t:

   4
  / \
 1   2

Return  false.

这道题比较简单。我的思路是 先找到大树S中 与 T的根结点值相同的结点，之后再来看 以这些结点为根结点的树 是否与T一样。

public boolean isSubtree(TreeNode s, TreeNode t) {
	List<TreeNode> rootNodes=new ArrayList<TreeNode>();
	DFS(s, rootNodes, t.val);
	for(TreeNode m:rootNodes){
		if(isSame(m, t)==true){
			return true;
		}
	}
	return false;
}

public void DFS(TreeNode node,List<TreeNode> list,int rootVal){
	if(node==null){
		return;
	}
	if(node.val==rootVal){
		list.add(node);
	}
	DFS(node.left,list,rootVal);
	DFS(node.right,list,rootVal);
}

public boolean isSame(TreeNode m,TreeNode n){
	if(m==null&&n==null){
		return true;
	}
	if(m!=null && n!=null){
		if(m.val!=n.val){
			return false;
		}
		else{
			return isSame(m.left, n.left) && isSame(m.right, n.right);
		}
	}
	else{
		return false;
	}
}

大神解法跟我类似，不过是遍历了S的每个结点，以每个结点来根，来与T树作比较。

public class Solution {
    public boolean isSubtree(TreeNode s, TreeNode t) {
        if (s == null) return false;
        if (isSame(s, t)) return true;
        return isSubtree(s.left, t) || isSubtree(s.right, t);
    }
    
    private boolean isSame(TreeNode s, TreeNode t) {
        if (s == null && t == null) return true;
        if (s == null || t == null) return false;
        
        if (s.val != t.val) return false;
        
        return isSame(s.left, t.left) && isSame(s.right, t.right);
    }
}

此外，还有一种解法：打出先根遍历的序列字符串，如果 S的字符串.contains(T的字符串) ，那么就是子树了。需要注意的是，先根遍历时，如果左右结点是空，也要打出来，不然会有问题。如下图：

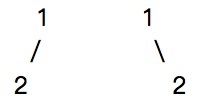
先根遍历的字符串都是 1,2，但是两棵树完全不同。必须要把空结点带上，才能区分。左边的树是 ,1,2,# ，右边的树是 ,1,#,2 ，这样就区分开来啦。

public boolean isSubtree(TreeNode s, TreeNode t) {
    return serialize(s).contains(serialize(t)); 
}

public String serialize(TreeNode root) {
    StringBuilder res = new StringBuilder();
    serialize(root, res);
    return res.toString();
}

private void serialize(TreeNode cur, StringBuilder res) {
    if (cur == null) {res.append(",#"); return;}
    res.append("," + cur.val);
    serialize(cur.left, res);
    serialize(cur.right, res);
}

当然，也有迭代用栈做先根遍历的。

public class Solution {
 public boolean isSubtree(TreeNode s, TreeNode t) {
        String spreorder = generatepreorderString(s); 
        String tpreorder = generatepreorderString(t);
        
        return spreorder.contains(tpreorder) ;
    }
    public String generatepreorderString(TreeNode s){
        StringBuilder sb = new StringBuilder();
        Stack<TreeNode> stacktree = new Stack();
        stacktree.push(s);
        while(!stacktree.isEmpty()){
           TreeNode popelem = stacktree.pop();
           if(popelem==null)
              sb.append(",#"); // Appending # in order to handle same values but not subtree cases
           else      
              sb.append(","+popelem.val);
           if(popelem!=null){
                stacktree.push(popelem.right);    
                stacktree.push(popelem.left);  
           }
        }
        return sb.toString();
    }
}

这道题有solutions： https://leetcode.com/problems/subtree-of-another-tree/solution/。方法就是我上面提到的两个方法。

Solution

---

Approach #1 Using Preorder Traversal [Accepted]

Algorithm

We can find the preorder traversal of the given tree $s$ and $t$, given by, say s_{preorder}s​preorder​​ and t_{preorder}t​preorder​​ respectively(represented in the form of a string). Now, we can check if t_{preorder}t​preorder​​ is a substring of s_{preorder}s​preorder​​.

But, in order to use this approach, we need to treat the given tree in a different manner. Rather than assuming a $null$ value for the childern of the leaf nodes, we need to treat the left and right child as a $lnull$ and $rnull$ value respectively. This is done to ensure that the t_{preorder}t​preorder​​ doesn't become a substring of s_{preorder}s​preorder​​ even in cases when $t$ isn't a subtree of $s$.

You can also note that we've added a '#' before every considering every value. If this isn't done, the trees of the form s:[23, 4, 5] and t:[3, 4, 5] will also give a true result since the preorder string of the t("23 4 lnull rull 5 lnull rnull") will be a substring of the preorder string of s("3 4 lnull rull 5 lnull rnull"). Adding a '#' before the node's value solves this problem.

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
public class Solution {
    HashSet < String > trees = new HashSet < > ();
    public boolean isSubtree(TreeNode s, TreeNode t) {
        String tree1 = preorder(s, true);
        String tree2 = preorder(t, true);
        return tree1.indexOf(tree2) >= 0;
    }
    public String preorder(TreeNode t, boolean left) {
        if (t == null) {
            if (left)
                return "lnull";
            else
                return "rnull";
        }
        return "#"+t.val + " " +preorder(t.left, true)+" " +preorder(t.right, false);
    }
}

Complexity Analysis

• Time complexity : O(m^2+n^2+m*n)O(m​2​​+n​2​​+m∗n). A total of $n$ nodes of the tree $s$ and $m$ nodes of tree $t$ are traversed. Assuming string concatenation takes $O(k)$ time for strings of length $k$ and indexOf takes $O(m\ast n)$.

• Space complexity : $O(max(m,n))$. The depth of the recursion tree can go upto $n$ for tree $t$ and $m$ for tree $s$ in worst case.

---

Approach #2 By Comparison of Nodes [Accepted]

Algorithm

Instead of creating an inorder traversal, we can treat every node of the given tree $t$ as the root, treat it as a subtree and compare the corresponding subtree with the given subtree $s$ for equality. For checking the equality, we can compare the all the nodes of the two subtrees.

For doing this, we make use a function traverse(s,t) which traverses over the given tree $s$ and treats every node as the root of the subtree currently being considered. It also checks the two subtrees currently being considered for their equality. In order to check the equality of the two subtrees, we make use of equals(x,y) function, which takes $x$ and $y$, which are the roots of the two subtrees to be compared as the inputs and returns True or False depending on whether the two are equal or not. It compares all the nodes of the two subtrees for equality. Firstly, it checks whether the roots of the two trees for equality and then calls itself recursively for the left subtree and the right subtree.

The follwowing animation depicts an abstracted view of the process:

Java

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */

public class Solution {
    public boolean isSubtree(TreeNode s, TreeNode t) {
        return traverse(s,t);
    }
    public boolean equals(TreeNode x,TreeNode y)
    {
        if(x==null && y==null)
            return true;
        if(x==null || y==null)
            return false;
        return x.val==y.val && equals(x.left,y.left) && equals(x.right,y.right);
    }
    public boolean traverse(TreeNode s,TreeNode t)
    {
        return  s!=null && ( equals(s,t) || traverse(s.left,t) || traverse(s.right,t));
    }
}

Complexity Analysis

• Time complexity : $O(m\ast n)$. In worst case(skewed tree) traverse function takes $O(m\ast n)$ time.

• Space complexity : $O(n)$. The depth of the recursion tree can go upto $n$. $n$ refers to the number of nodes in $s$.