机器学习总结6_支持向量机(SVM)

0.

支持向量机，非常非常非常经典的一个算法。看起来也特别费劲，看SVM的时候先别有一次性就能全面整明白的准备，可能要反反复复看许多不同的文章不同的资料，或许某一天，一切都明朗了。然后你会发现，之前的所有挣扎所有努力都是值得的，真的是很有启发性。
我不准备具体写SVM算法的整个流程。因为我感觉我写也写不好，写不好就怕给这个算法粘上一些污点，所以我想推荐一些文章和视频：

1.july大神的支持向量机通俗导论（理解SVM的三层境界）
http://blog.csdn.net/v_july_v/article/details/7624837
2.台湾大学《机器学习技法》，第一讲到第六讲。(台湾大学的《机器学习基石》和《机器学习技法》这两门课真的值得用心去看看的。)
http://mooc.guokr.com/course/1843/%E6%A9%9F%E5%99%A8%E5%AD%B8%E7%BF%92%E6%8A%80%E6%B3%95–Machine-Learning-Techniques-/
3.其他的资料百度一搜能搜很多，无数人写了关于SVM的资料。我觉得很多人都在按照自己的方式在写文章写书，你可以去看很多文章，寻到一个你最能引起共鸣的思路。

1

我还是忍不住要再写点东西，因为我当时在看SVM的时候，被几个问题困扰了很长时间。注意：接下来的只是补充，没有详细的介绍。
这里是假设“你已经把july的文章或者那六讲视频已经仔细看了”！！！！

关于KKT条件，当对偶问题的解满足KKT条件时，就可以说对偶问题的解和原始问题的解相同，同时都是最优解。问题来了，在对偶问题求解的过程中，是怎么满足KKT条件的？换句话说，为什么对偶问题求出来的解是满足KKT条件的？这个问题困扰了我好长好长时间。
KKT条件：

相信你如果看过SVM，你会对这4个条件感到很熟悉。
回去翻一翻SVM的讲解文章，你会发现在对偶问题的求解中，只有第二个和第三个条件作为对偶问题的约束条件一直在伴随左右，而第一个和第四个条件在对偶问题的求解中一直都没有出现。第一个和第四个条件在对偶问题的求解中并没有作为约束条件出现，那又怎么保证对偶问题的解就一定会满足这两个条件呢？
先看对偶问题的式子：

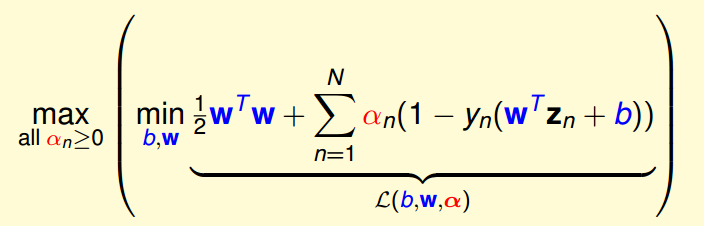
先看括号里面的最小化：
$min_{b,w}1/2w^Tw+\sum_{n=1}^{N}{a_n(1-Y_n(w^Tz_n+b))}$，这里只有$a_n>=0$这一个条件，没有关于w和b的约束条件。
可以想一下这个最小化的结果里，$(1-Y_n(w^Tz_n+b))一定要取的尽量小$，这时候又因为没有关于w和b的约束条件，所以不可能出现$(1-Y_n(w^Tz_n+b))$大于0的情况。这个最小化的结果应该是：$1/2w^Tw+\sum_{n=1}^{N}{a_n(-\infty)}$。

然后再对这个结果求最大值，接着就要保证$a_n(1-Y_n(w^Tz_n+b))=0$才能求出最大值（0显然是比负数要大的）。
总结一下：你就会发现KKT的第一个和第四个条件隐藏在了最优化的过程中，即$(1-Y_n(w^Tz_n+b))<=0$和$a_n(1-Y_n(w^Tz_n+b))=0$。

这个只是大概的说明，并不算是严格的证明，甚至说明的都有点牵强了。非常欢迎有人能对这个问题提出自己的理解。

2、Kernel 核技巧

这个真的是一个非常强大的工具，而且它也具有很强的启发性和扩展性。
核技巧的重点就是核函数，通过核函数，可以在样本的原始特征空间中直接计算样本映射到高维特征空间后之间的内积。
关于核技巧： 《机器学习技法》做了详细的说明。
我觉得对核技巧的理解可以有两种：
1. 我们可以把它理解成一种特征空间的映射，从低维特征空间映射到高维特征空间。
2. 我更喜欢把它理解成是重构样本的过程。
这两种理解并不矛盾，只是角度不同。

---

我说一下第二点：
这种理解的最关键一点就是：明确内积可以一定程度表示相似度。
！！！两个向量的内积可以在一定程度上去衡量这两个向量的相似度。仔细想想是不是有点道理。
现在每一个样本看成一个向量，我们可以从所有样本中均匀的选取一些关键样本，然后用每个样本和这些关键样本的内积去重新表示这个样本。
举个例子：
现在有10个样本X1，。。。。X10
我从这10个样本中，选出了3个关键样本，X2，X5，X9
这个时候样本X1就可以表示成 ( (X1,X2), (X1,X5), (X1,X9) )这样一个三维向量了，这个时候X1的特征就变成了3维的了。这个时候的样本的特征个数就是由你选择的关键点的个数决定的了。
同样X2可以表示成( (X2,X2), (X2,X5), (X2,X9) )这样一个三维向量。这就是通过样本之间的相似性去重构样本的特征空间。
而核函数实际上就是计算样本直接的内积的。所以我们就可以通过核函数对样本空间进行重构。同样是假设现在有10个样本X1，。。。。X10
我从这10个样本中，选出了3个关键样本，X2，X5，X9
这个时候样本X1就可以表示成 ( K(X1,X2), K(X1,X5), K(X1,X9) )这样一个三维向量了，这个时候X1的特征就变成了3维的了。
同样X2可以表示成( K(X2,X2), K(X2,X5), K(X2,X9) )这样一个三维向量。

我看到过很多篇用这种方法对特征空间进行重构的论文，而且我也在自己的论文中用到了这种技巧。通过kmeans算法选取关键点，然后通过核函数重构样本空间。
这种技巧真正强大的地方是在，假设你现在有个线性回归的实现代码，你不需要对线性回归的代码做任何更改，只需要通过高斯核函数对样本的特征空间进行重构，就可以实现在无穷维的特征空间中学习回归模型。对最原始的样本来说，现在所学习到的模型就不是线性模型了。
（平时如果我们想做一个二次回归，大部分时候都是对样本先做二次变换，然后再跑一遍线性回归，所做出来的模型就是二次回归模型了）

！！始终明确一点：核函数计算的是两个向量的内积，内积可以一定程度表示相似度。
！！始终明确一点：核函数计算的是两个向量的内积，内积可以一定程度表示相似度。
！！始终明确一点：核函数计算的是两个向量的内积，内积可以一定程度表示相似度。

这样就是说在你所优化的式子中并没有出现向量内积的时候，你也可以把核技巧加入进去。(因为W始终可以表示成样本的线性组合)

很难把这种理解讲的非常清楚，你可以带着这种理解去看一下《机器学习技法》。特别是如果你正在为论文发愁，你非常有必要去看一下，看能不能寻找到一些启发。

---

3.

惯例，先挖坑，有空再仔细改。