BP神经网络,全称为Backpropagation Neural Network,是人工神经网络的一种典型模型,主要用于非线性数据的分类和预测任务。这种网络结构基于反向传播的学习算法,通过不断调整权重来最小化预测误差,从而提高预测准确性。
BP神经网络隐层节点数的确定是神经网络设计中非常重要的一个环节,一个具有无限隐层节点的两层 BP 网络可以实现任意从输入到输出的非线性映射。但对于有限个输入到输出的映射,并不需要无限个隐层节点,这就涉及到如何选择隐层节点数的问题。
一般有如下三种方法确定:
构造法
首先运用三种确定隐含层层数的方法得到三个隐含层层数,找到最小值和最大值,然后从最小值开始逐个验证模型预测误差,直到达到最大值。最后选取模型误差最小的那个隐含层层数。该方法适用于双隐含层网络。
删除法
单隐含层网络非线性映射能力较弱,相同问题,为达到预定映射关系,隐层节点要多一些,以增加网络的可调参数,故适合运用删除法。
黄金分割法
算法的主要思想:首先在[a,b]内寻找理想的隐含层节点数,这样就充分保证了网络的逼近能力和泛化能力。为满足高精度逼近的要求,再按照黄金分割原理拓展搜索区间,即得到区间b,c,在区间[b,c]中搜索最优,则得到逼近能力更强的隐含层节点数,在实际应用根据要求,从中选取其一即可。

BP算法中,权值和阈值是每训练一次,调整一次。逐步试验得到隐层节点数就是先设置一个初始值,然后在这个值的基础上逐渐增加,比较每次网络的预测性能,选择性能最好的对应的节点数作为隐含层神经元节点数。
一般在BP网络编程时,我们基本是随意指定一个隐藏层节点数比如6或者10,对网络的准确率有一定影响,为此本文采用编程的方式确定了最佳隐藏层节点数目。对应BP神经网络的正确运用提供了参考。
02 效果图展示:
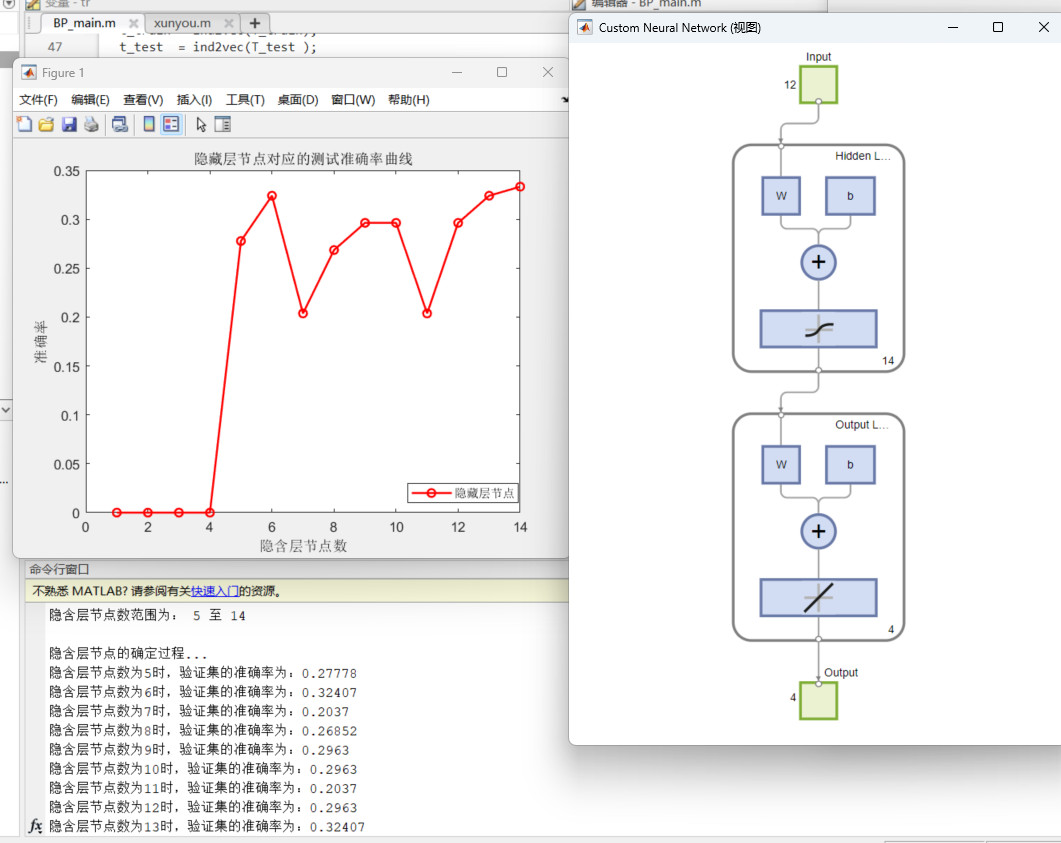
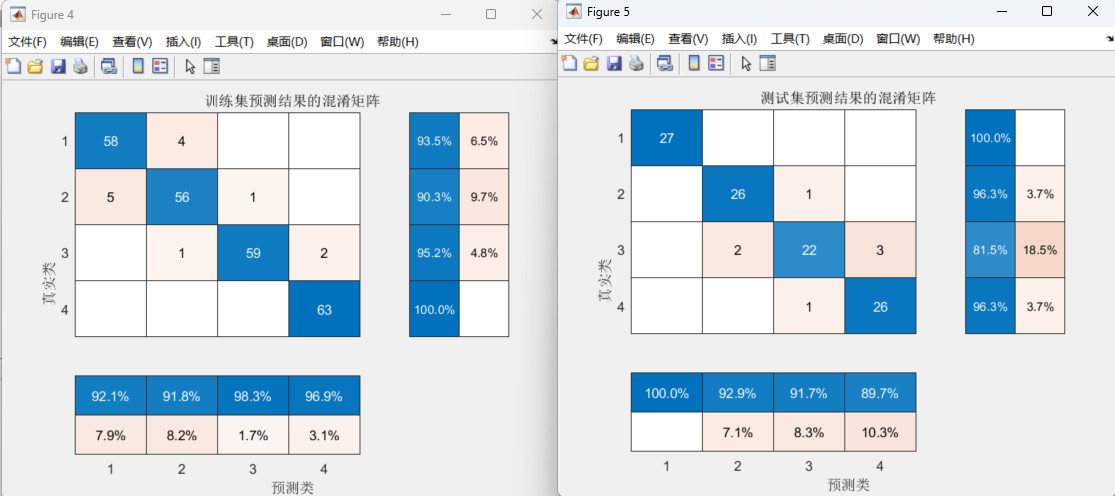
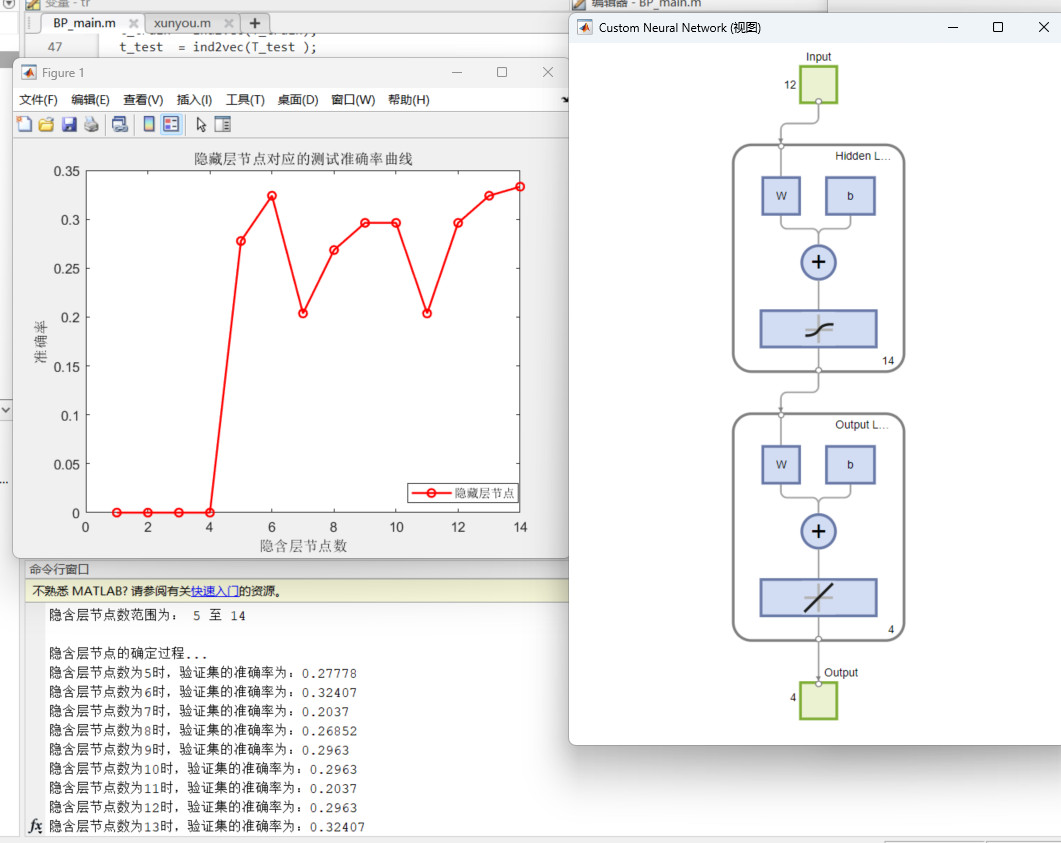
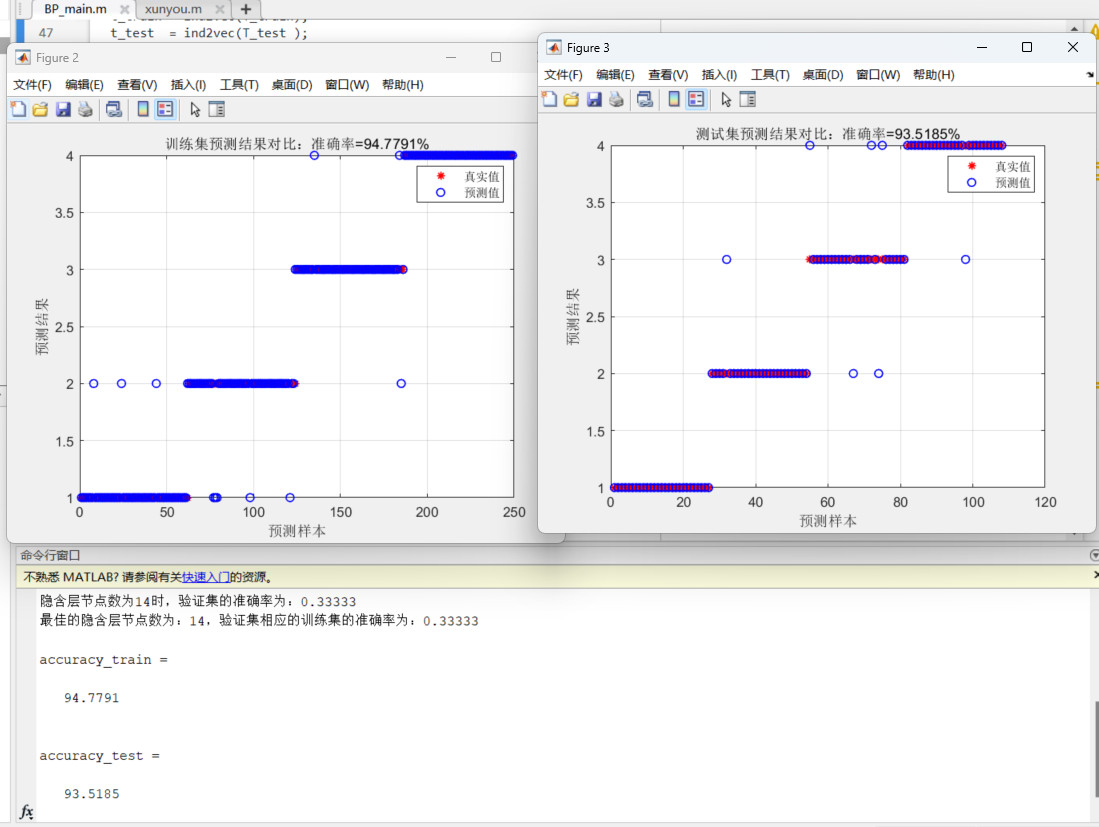
























 463
463

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








