【basalt】（一）3D点参数化

basalt 使用2D-dir和inverse-depth对3D点进行参数化，相比VINS只优化逆深度的方式，这种参数化方式更加合理，host帧对点的方向观测确实应该优化一下

---

1、3D点参数化

XYZ形式的3D点参数化：
$$P=\left[\begin{array}{c}X\\ Y\\ Z\\ 1\end{array}\right]$$

表示成逆深度的形式：
$$P=\left[\begin{array}{c}X/d\\ Y/d\\ Z/d\\ 1/d\end{array}\right],d=\sqrt{X^2+Y^2+Z^2}$$

前三维是单位向量，表示3D点的方向，后一维是逆深度，如果想使用这种方式参数化3D点，显然有一个自由度是多于的，有两种处理方式：
1）采用类似VINS的方法，3D点的方向由host frame的对该3D点的观测来构造，这种方式导致无法对3D点的观测方向进行优化
2）通过stereographic projection将前三维单位向量参数化成2D-dir的形式，从而能够对2D-dir进行优化

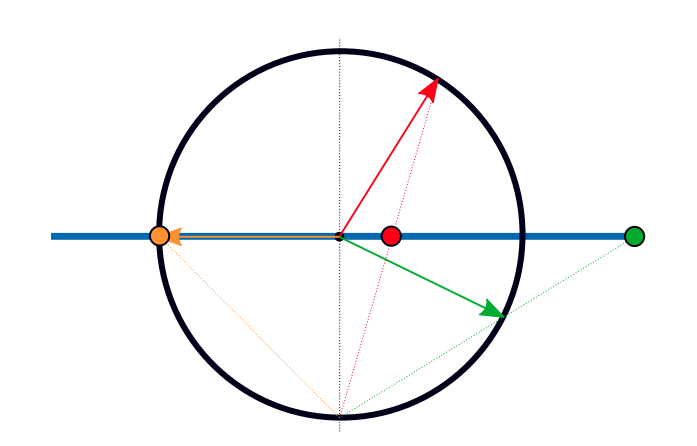
$\mathbf{P}(x,y,z)$ 是3D点单位化的向量（unit-length bearing vector），位于上图黑色的单位球上

$\mathbf{p}(u,v)$ 是对 $\mathbf{P}(x,y,z)$ 通过stereographic投影得到的2D-dir（注意，$(u,v)$ 不是像素坐标），位于上图中蓝色2D平面上

1.1 stereographic投影

将空间中一个3D点$\mathbf{P}$归一化到单位圆上，然后根据三角形相似，将单位球上的一点投影到平面上，即：
$$\begin{array}{rl}\mathbf{p}=\pi (\mathbf{P})& =\left[\begin{array}{c}\frac{x/d}{1+z/d}\\ \frac{y/d}{1+z/d}\end{array}\right]=\left[\begin{array}{c}\frac{x}{d+z}\\ \frac{y}{d+z}\end{array}\right]\end{array}$$

其中$d=\sqrt{x^2+y^2+z^2}$.

代码里对3D点齐次坐标$P_{homogeneous}$（$4\times 1$）做stereographic projection时，直接取了$P_{homogeneous}$的$\text{2-norm}$，显然它不是深度（应该是手误的bug…），而是：
$$\text{2-norm}=\sqrt{(x/d{)}^2+(y/d{)}^2+(z/d{)}^2+(1/d{)}^2}=\sqrt{1+(1/d{)}^2}$$

其中，代码里三角化得到的3D点为$P_{normalize}=[x/d,y/d,z/d,1/d{]}^T$，前三维是已经归一化后3D点坐标.

1.2 stereographic反投影

反投影得到
$$\begin{array}{rl}{\mathbf{P}}_{\mathbf{sphere}}={\pi }^{-1}(\mathbf{p})& =\frac{2}{1+u^2+v^2}\left[\begin{array}{c}u\\ v\\ 1\end{array}\right]-\left[\begin{array}{c}0\\ 0\\ 1\end{array}\right]\end{array}$$

反投影函数对 $\mathbf{p}$ 的雅可比矩阵记为 $J_{up}^{4\times 2}$，最后一行只与逆深度有关，补零即可.

---

2、重投影雅可比

由于参数化后的3D点由2D-dir和一个inverse-depth构成，所以先要恢复出3D点:
$$P_{normlize}=[P_{sphere},1/d{]}^T$$

其中，前三维直接由stereographic反投影得到，最后一维为逆深度

接着，根据相机模型构造如下重投影误差：
$$\begin{array}{rl}e& ={\pi }_{cam-model}\left(T_{th}{P}_{normlize}\right)-\left[\begin{array}{c}{u}_{obs}\\ v_{obs}\end{array}\right]\\ & ={\pi }_{cam-model}\left(T_{th}\left[\begin{array}{c}{\pi }_{stereographic}^{-1}(p_{2D-dir})\\ 1/d\end{array}\right]\right)-\left[\begin{array}{c}{u}_{obs}\\ v_{obs}\end{array}\right]\\ & =K{f}_{\text{normalize-plane}}\left(T_{th}\left[\begin{array}{c}{\pi }_{stereographic}^{-1}(p_{2D-dir})\\ 1/d\end{array}\right]\right)-\left[\begin{array}{c}{u}_{obs}\\ v_{obs}\end{array}\right]\end{array}$$

对$T_{th}$求雅可比：
$$\frac{\partial e}{\partial {\xi }_{th}}=\frac{\partial e}{\partial P_t}\ast \frac{\partial P_t}{\partial {\xi }_{th}}$$

对$p_{2D-dir}$的雅可比：
$$\frac{\partial e}{\partial p_{2D-dir}}=\frac{\partial e}{\partial P_t}\ast \frac{\partial P_t}{\partial P_{normlize}}\ast \frac{\partial P_{normlize}}{\partial p_{2D-dir}}=\frac{\partial e}{\partial P_t}\ast T_{th}^{3\times 4}\ast J_{up}^{4\times 2}$$

其中，$\frac{\partial P_t}{\partial P_{normlize}}=T_{th}$

对inverse-depth的雅可比：
$$\frac{\partial e}{\partial id}=\frac{\partial e}{\partial P_t}\ast \frac{\partial P_t}{\partial P_{normlize}}\ast \frac{\partial P_{normlize}}{\partial id}=\frac{\partial e}{\partial P_t}\ast T_{th}\ast \left[\begin{array}{c}0\\ 0\\ 0\\ 1\end{array}\right]=\frac{\partial e}{\partial P_t}\ast T_{th}^{col3}$$

---

@leatherwang

二零二零年六月十五日

---