【刚体运动几何】（一）刚体速度转换

参考：《A Mathematical Introduction to Robotic Manipulation》

疑问：

• 刚体的速度只有在选定坐标系时才有谈论意义，比如一台小车可以看作是一个刚体，其上有三个传感器，Camera有一个速度，IMU有一个速度，轮子有一个速度，首先它们的速度是不同的（比如把地球看作一个刚体，地心的速度与地球表面的速度是不同的），那么这些速度的关系是什么呢？
• VIO中为何不使用Camera系而是IMU作为body系，如果使用Camera作为body系，IMU的测量值（角速度和加速度）要如何转化到Camera坐标系下？

---

1. 转动速度

刚体上任意一点$q$在空间坐标系中的运动轨迹为：
$${\mathbf{q}}_a(t)={\mathbf{R}}_{ab}(t){\mathbf{q}}_b$$

其中，A为空间坐标系，B为物体坐标系，坐标${\mathbf{q}}_b$是在物体坐标系中固定不变的，该点在空间坐标系中的速度为：
$${\mathbf{v}}_{{\mathbf{q}}_a}(t)=\frac{d}{dt}{\mathbf{q}}_a(t)={\dot{\mathbf{R}}}_{ab}(t){\mathbf{q}}_b$$

因此，${\mathbf{R}}_{ab}$将一点的刚体坐标变换为该点的空间速度，类似${\mathbf{R}}_{ab}$这种表示需要九个参数，不是很方便，转换成下面的简洁形式：
$$v_{q_a}(t)={\dot{R}}_{ab}(t)R_{ab}^{-1}(t)R_{ab}(t)q_b$$

我们已经知道${\dot{R}}_{ab}(t)R_{ab}^{-1}(t)\in \mathrm{so}(3)$，是反对陈矩阵，记为：
$${\hat{\omega }}_{ab}^s:={\dot{R}}_{ab}{R}_{ab}^{-1}$$

其中，${\hat{\omega }}_{ab}^s$表示$b$系在$a$系下的速度在空间坐标系下的表示，描述为物体相对空间坐标系A的瞬时角速度

1.1 刚体上一点的速度（A系与B系之间只有纯旋转运动）

现在就可以使用物体的瞬时角速度来表示一点的速度，如下：
$$v_{q_a}(t)={\hat{\omega }}_{ab}^s{R}_{ab}(t)q_b={\omega }_{ab}^s(t)\times q_a(t)$$

对应的物理含义为：刚体的转速与刚体上一点到坐标系原点的距离的叉乘即为这一点的瞬时速度，$q_b$这个向量的长度越长，速度就越大，反之亦然，当长度为0时（该点与坐标系原点重合时），速度为0

这样，只要知道物体的瞬时角速度和物体坐标上任意一点的位置，就可以得到该点在空间坐标下的速度

1.2 （瞬时）物体坐标系下的转动速度

同理也可得到 ${\hat{\omega }}_{ab}^b$，如下：
$${\hat{\omega }}_{ab}^b:=R_{ab}^{-1}{\dot{R}}_{ab}$$

它描述的是相对于瞬时物体坐标系B的角速度（$b$系在$a$系下的速度在物体坐标系下的表示），该角速度可以直接通过陀螺仪直接测量得到

由以上两式可得两种角速度之间的关系：
$${\hat{\omega }}_{ab}^b=R_{ab}^{-1}{\hat{\omega }}_{ab}^s{R}_{ab}\text{ or }{\omega }_{ab}^b=R_{ab}^{-1}{\omega }_{ab}^s$$

因此，物体角速度为将空间角速度旋转到瞬时物体坐标系而得到的

2. 刚体速度

对于运动轨迹为为单参数曲线$g_{ab}(t)\in SE(3)$的一般情况
$$g_{ab}(t)=\left[\begin{array}{cc}{R}_{ab}(t)& p_{ab}(t)\\ 0& 1\end{array}\right]$$

可得，
$${\dot{g}}_{ab}{g}_{ab}^{-1}=\left[\begin{array}{cc}{\dot{R}}_{ab}& {\dot{p}}_{ab}\\ 0& 0\end{array}\right]\left[\begin{array}{cc}{R}_{ab}^T& -R_{ab}^T{p}_{ab}\\ 0& 1\end{array}\right]=\left[\begin{array}{cc}{\dot{R}}_{ab}{R}_{ab}^T& -{\dot{R}}_{ab}{R}_{ab}^T{p}_{ab}+{\dot{p}}_{ab}\\ 0& 0\end{array}\right]$$

定义$V_{ab}^s\in se(3)$表示$b$系在$a$系下的速度在空间坐标系下的表示
$${\hat{V}}_{ab}^s={\dot{g}}_{ab}{g}_{ab}^{-1},V_{ab}^s=\left[\begin{array}{c}{v}_{ab}^s\\ {\omega }_{ab}^s\end{array}\right]=\left[\begin{array}{c}-{\dot{R}}_{ab}{R}_{ab}^T{p}_{ab}+{\dot{p}}_{ab}\\ {\left({\dot{R}}_{ab}{R}_{ab}^T\right)}^{\vee }\end{array}\right]$$

虽然$V_{ab}^s\in se(3)$，但这里的移动分量$v_{ab}^s$却是以m/s为单位的平移速度，因为${\dot{p}}_{ab}$的单位是m/s

注意，移动分量 $v_{ab}^s(t)$ 并不是刚体坐标系原点的速度，而是刚体上一点在$t$时刻经过空间坐标系原点时（可能是想象的）的速度。即，如果一个人站在空间坐标系的原点处去测量刚体上正好经过原点的一点的瞬时速度，那么该瞬时速度即为$v_{ab}^s(t)$

2.1 刚体上一点的速度

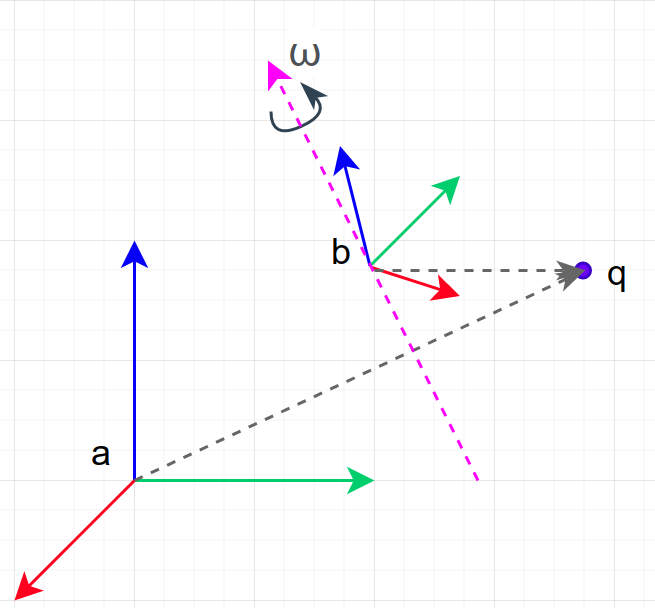
在空间坐标系中，固联在刚体上的一点$q$的坐标为
$$q_a(t)=g_{ab}(t)q_b$$

两边微分得
$$v_{q_a}={\dot{q}}_a={\dot{g}}_{ab}{q}_b={\dot{g}}_{ab}{g}_{ab}^{-1}{q}_a$$

进一步得到
$$v_{q_a}={\hat{V}}_{ab}^s{q}_a={\omega }_{ab}^s\times q_a+v_{ab}^s$$

其中，$v_{q_a}$由两部分构成，${\omega }_{ab}^s\times q_a$表示因旋转产生的速度，$v_{ab}^s$表示平移产生的速度，两个向量相加即为最终的合成速度

2.2 （瞬时）物体坐标系下的刚体速度

向量可以直接通过坐标系之间旋转外参进行转换

由于$v_{q_a}$是向量，使用旋转矩阵进行转换，可得物体坐标系中一点的速度为：
$$\left[\begin{array}{c}{v}_{q_b}\\ 0\end{array}\right]=g_{ab}^{-1}\left[\begin{array}{c}{v}_{q_a}\\ 0\end{array}\right]$$

忽略矩阵维度，简写成：
$$v_{q_b}=g_{ab}^{-1}{v}_{q_a}=g_{ab}^{-1}{\dot{g}}_{ab}{q}_b={\hat{V}}_{ab}^b(t)q_b$$

物体坐标系下的刚体速度定义为：
$${\hat{V}}_{ab}^b=g_{ab}^{-1}{\dot{g}}_{ab}=\left[\begin{array}{cc}{R}_{ab}^T{\dot{R}}_{ab}& R_{ab}^T{\dot{p}}_{ab}\\ 0& 0\end{array}\right],V_{ab}^b=\left[\begin{array}{c}{v}_{ab}^b\\ {\omega }_{ab}^b\end{array}\right]=\left[\begin{array}{c}{R}_{ab}^T{\dot{p}}_{ab}\\ {\left(R_{ab}^T{\dot{R}}_{ab}\right)}^{\vee }\end{array}\right]$$

需要指出的是，物体速度并不是物体相对于物体坐标系的速度（此速度总是零）

2.3 空间坐标下的刚体速度与（瞬时）物体坐标系下的刚体速度的关系

$${\hat{V}}_{ab}^s={\dot{g}}_{ab}{g}_{ab}^{-1}=g_{ab}\left(g_{ab}^{-1}{\dot{g}}_{ab}\right)g_{ab}^{-1}=g_{ab}{\hat{V}}_{ab}^b{g}_{ab}^{-1}$$

可得，
$$V_{ab}^s=\left[\begin{array}{c}{v}_{ab}^s\\ {\omega }_{ab}^s\end{array}\right]=\left[\begin{array}{cc}{R}_{ab}& {\hat{p}}_{ab}{R}_{ab}\\ 0& R_{ab}\end{array}\right]\left[\begin{array}{c}{v}_{ab}^b\\ {\omega }_{ab}^b\end{array}\right]=\mathbf{Ad}(g_{ab})V_{ab}^b$$

3. 刚体速度的坐标转换

假如知道了IMU与底盘坐标系之间的外参以及IMU的速度，如何得到底盘坐标系的速度

3.1 空间坐标系下的转换

假设存在A、B、C三个坐标系，它们在空间坐标系下的刚体速度存在下述关系：
$$\begin{array}{rl}{\hat{V}}_{ac}^s& ={\dot{g}}_{ac}{g}_{ac}^{-1}\\ & =\left({\dot{g}}_{ab}{g}_{bc}+g_{ab}{\dot{g}}_{bc}\right)\left(g_{bc}^{-1}{g}_{ab}^{-1}\right)\\ & ={\dot{g}}_{ab}{g}_{ab}^{-1}+g_{ab}\left({\dot{g}}_{bc}{g}_{bc}^{-1}\right)g_{ab}^{-1}\\ & ={\hat{V}}_{ab}^s+g_{ab}{\hat{V}}_{bc}^b{g}_{ab}^{-1}\end{array}$$

注意，这里使用的是${\hat{V}}_{bc}^b$，而书里面使用的是${\hat{V}}_{bc}^s$，好像是书里写的有问题

转换成向量的形式，
$$V_{ac}^s=V_{ab}^s+\mathbf{Ad}(g_{ab})V_{bc}^b$$

如果$g_{bc}$是常量，相当于刚体上两个坐标系B和C之间的外参，此时二者的速度关系为
$$V_{ac}^s=V_{ab}^s$$

由于两个坐标系B和C同属于一个刚体，所以两个坐标系B和C在空间坐标系下的刚体速度是相同的

将上式转换到物体坐标系
$$\begin{array}{r}\mathbf{Ad}(g_{ac})V_{ac}^c=\mathbf{Ad}(g_{ab})V_{ab}^s\\ V_{ac}^c=\mathbf{Ad}(g_{ac}{)}^{-1}\mathbf{Ad}(g_{ab})V_{ab}^s\\ V_{ac}^c=\mathbf{Ad}(g_{cb})V_{ab}^s\end{array}$$

即，刚体上两个坐标系B和C在各自的物体坐标系下的刚体速度关系

3.2 物体坐标系下的转换

同理可得，
$$\begin{array}{rl}{\hat{V}}_{ac}^c& =g_{ac}^{-1}{\dot{g}}_{ac}\\ & =\left(g_{bc}^{-1}{g}_{ab}^{-1}\right)\left({\dot{g}}_{ab}{g}_{bc}+g_{ab}{\dot{g}}_{bc}\right)\\ & =g_{bc}^{-1}{g}_{ab}^{-1}{\dot{g}}_{ab}{g}_{bc}+g_{bc}^{-1}{\dot{g}}_{bc}\\ & =g_{bc}^{-1}{\hat{V}}_{ab}^b{g}_{bc}+{\hat{V}}_{bc}^c\end{array}$$

转换成向量的形式，
$$V_{ac}^c=\mathbf{Ad}(g_{bc}^{-1})V_{ab}^b+V_{bc}^c$$

如果$g_{bc}$是常量，相当于刚体上两个坐标系B和C之间的外参，此时二者的速度关系为
$$V_{ac}^c=\mathbf{Ad}(g_{bc}^{-1})V_{ab}^b$$

---

@leatherwang

二零二零年九月二十日

---