任意信号在完备正交函数系中的表示法

1. 信号的正交分解

信号分解的目的：1. 将任意信号分解为单元信号之和，从而考察信号的特性
\quad \quad \quad \quad \quad \quad \quad 2. 简化电路分析与计算，总响应=单元响应之和

1. 矢量的正交分解

1. 分解原则：剩余部分的误差分量最小
   
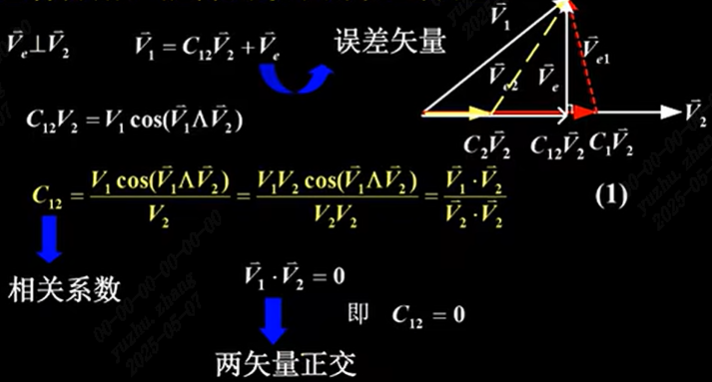
2. 正交分解
   平面中任一矢量可分解为x，y二方向矢量
   空间中任一矢量可分解为x，y，z三方向矢量
   一个三维空间矢量必须用三个正交矢量来表示，如果用二维矢量表示会出现误差

2. 信号的正交分解

$f_1(t),f_2(t)$为任意两个信号
$f_1(t)=C_{12}{f}_2(t)+f_e(t)$
若$f_1(t)\approx C_{12}{f}_2(t)$ 则：
误差函数 $f_e(t)=f_1(t)-C_{12}{f}_2(t)$
分解原则：$f_e(t)$的方均值最小，即误差信号功率（能量）最小
求相关系数：误差函数方均值最小时求出相关系数 $C_{12}$


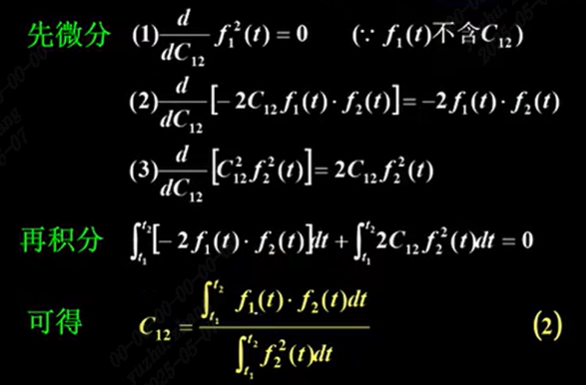
比较公式(1)和(2)，分解的原则对应：即$f_e(t)$的方均值
若$C_{12}=0$，此时$f_1(t),f_2(t)$称为正交函数，满足${\int }_{t_1}^{t_2}{f}_1(t)\cdot f_2(t)dt$
几点认识：
$\bullet f_e(t)与f_2(t)$正交，因为$f_1(t)$中已最大限度抽出$f_2(t)$，已无$f_2(t)$分量
$\bullet f_1(t)$中还可以抽出除$f_2(t)$以外的函数，如$f_3(t)$，此时，$f_1(t)=C_{12}{f}_2(t)+C_{13}{f}_3(t)+f_{e1}(t)$
$f_{e1}(t):$抽出$f_2(t),f_3(t)$后剩下的误差函数
总结
$\bullet$两周期信号在同一周期内（同区间内）正交（即从$f_1(t)$中抽不出$f_2(t)$分量）的条件是$C_{12}=0$，即：${\int }_{t_1}^{t_2}{f}_1(t)\cdot f_2(t)dt=0$
$\bullet$对一般信号在给定区间正交，而在其他区间不一定满足正交
$\bullet$两个信号不正交，就有相关关系，必能抽出另一信号

3. 正交函数集

任意信号f(t)可表示为n维正交函数之和：
$f(t)\equiv C_1{g}_1(t)+C_2{g}_2(t)+...+C_r{g}_r(t)+...+C_n{g}_n(t)={\sum }_{r=1}^n{C}_r{g}_r(t)$
原函数 \quad \quad \quad \quad \quad \quad 近似函数
$g_1(t),g_2(t),...,g_n(t)$相互正交

复变函数的正交特性

在区间$(t_1,t_2)$内，若复变函数集$g_r(t),(r=0,1,2,...,n)$满足以下关系：
${\int }_{t_1}^{t_2}{g}_i(t)g_j^{\ast }(t)dt=0i\ne j$
${\int }_{t_1}^{t_2}{g}_i(t)g_i^{\ast }(t)dt=K_i$
则此复变函数集为正交函数集
用$g_r(t),(r=0,1,...,n)$表示f(t)，求相关系数$C_r=\frac{{\int }_{t_1}^{t_2}f(t)g_r^{\ast }(t)dt}{{\int }_{t_1}^{t_2}{g}_r(t)g_r^{\ast }(t)dt}$, $g_r^{\ast }(t)为g_r(t)$的共轭

4. 完备正交函数集

$f(t)\equiv C_1{g}_1(t)+C_2{g}_2(t)+...+C_r{g}_r(t)+...+C_n{g}_n(t)={\sum }_{r=1}^n{C}_r{g}_r(t)$
**定义1：**当n增加时，$\overline{{ϵ}^2}$下降，若$n\to \infty$，则$\overline{{ϵ}^2}\to 0$，此时$g_1(t),g_2(t),...,g_n(t)$为完备的正交函数集
**定义2：**如果存在函数x(t)，有${\int }_{t_1}^{t_2}{g}_r(t)\cdot x(t)dt=0$，则x(t)必属于此正交函数集，原函数集$g_1(t),g_2(t),...,g_n(t)$不完备，若不存在这样的x(t)，则此函数集为完备正交函数集

2. 功率信号和能量信号

定义：设i(t)为流过电阻R的电流，v(t)为R上的电压，瞬时功率为 $p(t)=i^2(t)R$，在一个周期内，R消耗的能量$W={\int }_{\frac{-T_0}{2}}^{\frac{T_0}{2}}p(t)dt=R{\int }_{\frac{-T_0}{2}}^{\frac{T_0}{2}}{i}^2(t)dt$或$W=\frac{1}{R}{\int }_{\frac{-T_0}{2}}^{\frac{T_0}{2}}{v}^2(t)dt$
平均功率可表示为：
$P=\frac{1}{T_0}R{\int }_{\frac{-T_0}{2}}^{\frac{T_0}{2}}{i}^2(t)dt$或$P=\frac{1}{T_0}\frac{1}{R}{\int }_{\frac{-T_0}{2}}^{\frac{T_0}{2}}{v}^2(t)dt$
**定义：**一般来说，能量总是与某一物理量的平方成正比。令R=1，则在整时间域内，实信号f(t)的
能量$W={\lim }_{T_0\to \infty }{\int }_{\frac{-T_0}{2}}^{\frac{T_0}{2}}{f}^2(t)dt$，
平均功率$P={\lim }_{T_0\to \infty }\frac{1}{T_0}{\int }_{\frac{-T_0}{2}}^{\frac{T_0}{2}}{f}^2(t)dt$
讨论上面两个式子，一般会出现两种情况：

1. $0<W<\infty$（有限值）P=0
2. $0<P<\infty$（有限值）W=$\infty$
   满足1式的称为能量信号，满足2式的称为功率信号
   一般规律：
3. 一般周期信号为功率信号
4. 非周期信号，在有限区间有值，为能量信号
5. 还有一些非周期信号，也是非能量信号，如u(t)是功率信号，tu(t)为非功率非能量信号，$\delta (t)$是无定义的非功率非能量信号

帕斯瓦尔定理