Table of Contents
from IPython.core.interactiveshell import InteractiveShell
InteractiveShell.ast_node_interactivity = "all"
本内容只用作笔记和学习分享,来自DataWhale与《统计学习方法》2nd
Chap 3 K-Nearist Neighbor (KNN,K近邻法)
K近邻法是基本的分类与回归方法。
以分类问题为例:
- 输入:实例的特征向量
- 分类决策:根据其k个最近邻的训练实例的类别,以
多数表决等方式进行预测 - 输出:实例类别
实质为:利用训练数据集对特征向量空间进行划分,并作为分类的模型
三大基本要素:
- k值的选择
- 距离度量
- 分类决策规则
K近邻法介绍
k-NN 算法
输入:训练数据集
T
=
(
x
1
,
y
1
)
,
(
x
2
,
y
2
)
,
.
.
.
,
(
x
N
,
y
N
)
T = {(x_1,y_1),(x_2,y_2),...,(x_N,y_N)}
T=(x1,y1),(x2,y2),...,(xN,yN)
其中,
x
i
∈
χ
⊆
R
n
x_i\in\chi\subseteq{R^n}
xi∈χ⊆Rn为实例的特征向量,
y
i
∈
Y
=
c
1
,
c
2
,
.
.
.
,
c
k
y_i\in{Y} = {c_1,c_2,...,c_k}
yi∈Y=c1,c2,...,ck为实例的类别,
i
=
1
,
2
,
.
.
.
,
N
i = 1,2,...,N
i=1,2,...,N;
输出:实例x所属的类y
1) 根据给定的距离变量,在训练集 T T T中找出与 x x x最邻近的 k k k个点,涵盖这 k k k个点的 x x x的领域记作 N k ( x ) N_k(x) Nk(x)
2) 在 N k ( x ) N_k(x) Nk(x)中根据分类决策规则决定 x x x的类别 y y y;
p
^
=
arg
max
c
j
∑
x
i
∈
N
k
(
x
)
I
(
y
i
=
c
j
)
,
i
=
1
,
2
,
.
.
.
,
N
;
j
=
1
,
2
,
.
.
.
,
K
(3.1)
\begin{aligned} \hat{p} &= \mathop{\arg\max} \limits_{c_j} \sum_{x_i\in{N_k(x)}}{I(y_i = c_j)},i = 1,2,...,N; j = 1,2,...,K \end{aligned} \tag{3.1}
p^=cjargmaxxi∈Nk(x)∑I(yi=cj),i=1,2,...,N;j=1,2,...,K(3.1)
在(3.1)中,
I
I
I为指示函数,即当
y
i
=
c
j
y_i=c_j
yi=cj时
I
I
I为1,否则
I
I
I为0
当k=1时,则称为最近邻算法;也就是对于输入的实例点 x x x,最近邻法将训练数据集中与 x x x最近的类作为 x x x的类
模型
k-NN法中,在k值、距离度量方式、分类决策规则以及训练数据集给定之后,对于任何一个新的输入实例,其所属的类唯一确定。
特征空间中,对每个训练实训点
x
i
x_i
xi,距离该点比其他更近的所有点组成一个区域,称为单元,每个训练实例点拥有一个单元。
所有训练实例点的单元构成对特征空间的一个划分
距离度量
特征空间中两个实例点的距离是两个实例点相似程度的反映。
k k k近邻模型的特征模型一般是 n n n维实数向量空间 R n R^n Rn。
使用欧氏距离,即一般的 L p L_p Lp距离取 p = 2 p=2 p=2
假设特征空间 χ \chi χ是 n n n维实数向量空间 R n R^n Rn, x i , x j ∈ χ x_i,x_j\in\chi xi,xj∈χ, x i = ( x i ( 1 ) , x i ( 2 ) , . . . , x i ( n ) ) T , x j = ( x j ( 1 ) , x j ( 2 ) , . . . , x j ( n ) ) T , x_i = (x_i^{(1)},x_i^{(2)},...,x_i^{(n)})^\mathrm{T},x_j = (x_j^{(1)},x_j^{(2)},...,x_j^{(n)})^\mathrm{T}, xi=(xi(1),xi(2),...,xi(n))T,xj=(xj(1),xj(2),...,xj(n))T,
x i , x j x_i,x_j xi,xj的 L p L_p Lp距离定义为:
L p ( x i , x j ) = ( ∑ t = 1 n ∣ x i ( l ) − x j ( l ) ∣ p ) 1 p (3.2) L_p(x_i,x_j) = (\sum_{t=1}^n{\left|x_i^{(l)}-x_j^{(l)} \right|}^p)^\frac{1}{p} \tag{3.2} Lp(xi,xj)=(t=1∑n xi(l)−xj(l) p)p1(3.2)
p=1时,称为曼哈顿距离
L 1 ( x i , x j ) = ( ∑ t = 1 n ∣ x i ( l ) − x j ( l ) ∣ ) (3.2) L_1(x_i,x_j) = (\sum_{t=1}^n{\left|x_i^{(l)}-x_j^{(l)} \right|}) \tag{3.2} L1(xi,xj)=(t=1∑n xi(l)−xj(l) )(3.2)
p=2时,称为欧氏距离
L 2 ( x i , x j ) = ( ∑ t = 1 n ∣ x i ( l ) − x j ( l ) ∣ 2 ) 1 2 (3.2) L_2(x_i,x_j) = (\sum_{t=1}^n{\left|x_i^{(l)}-x_j^{(l)} \right|}^2)^\frac{1}{2} \tag{3.2} L2(xi,xj)=(t=1∑n xi(l)−xj(l) 2)21(3.2)
k值选择
k值较小
学习的近似误差减小,但估计误差会增大,预测结果对近邻的实例点更加敏感;整体模型会变得复杂,容易出现过拟合
k值较大
减少估计误差,但增大了近似误差,与输入实例较远的训练实例也会对预测起作用;模型变得相对简单
实际应用
一般选择一个较小的数值,采用交叉验证法来选取最优的
k
k
k值
分类决策规则
多数表决规则(majority voting rule):
如果分类的损失函数为0-1损失函数,则分类函数为:
f
:
R
n
→
{
c
1
,
c
2
,
.
.
.
,
c
K
}
f:R^n \rightarrow \{c_1,c_2,...,c_K\}
f:Rn→{c1,c2,...,cK}
则误分类的概率为
P
(
Y
≠
f
(
X
)
)
=
1
−
P
(
Y
=
f
(
X
)
)
P(Y\neq{f(X)}) = 1 - P(Y = f(X))
P(Y=f(X))=1−P(Y=f(X))
对给定实例 x ∈ χ x\in\chi x∈χ,其最近邻的 k k k个训练实例点构成集合 N k ( x ) N_k(x) Nk(x),如果覆盖 N k ( x ) N_k(x) Nk(x)的区域分类是 c j c_j cj,则误分类率是
1 k ∑ x i ∈ N k ( x ) I ( y i ≠ c j ) = 1 − 1 k ∑ x i ∈ N k ( x ) I ( y i = c j ) \frac{1}{k}\sum_{x_i\in{N_k(x)}}I(y_i \neq c_j)=1 - \frac{1}{k}\sum_{x_i\in{N_k(x)}}I(y_i = c_j) k1xi∈Nk(x)∑I(yi=cj)=1−k1xi∈Nk(x)∑I(yi=cj)
要求误分类率最小,即经验风险最小,则要求 1 k ∑ x i ∈ N k ( x ) I ( y i = c j ) \frac{1}{k}\sum_{x_i\in{N_k(x)}}I(y_i = c_j) k1∑xi∈Nk(x)I(yi=cj)最大
故多数表决规则等价于经验风险最小化
实现 ->> kd树
考虑问题:如何对训练数据集进行快速的k近邻搜索
-
在特征空间维数大及训练数据容量大时尤为重要
-
最简单实现方式:线性扫描(linear scan)
-
为了提升效率,则可以考虑使用特殊结构来存储训练数据,以减少计算距离的次数
构造kd树
k
d
kd
kd树是一种对
k
k
k维空间中的实例点进行存储以便对其进行快速检索的树形数据结构,属于二叉树结构。
表示对
k
k
k维空间的一个划分,等价于不断地用垂直于坐标轴的超平面将
k
k
k维空间切分,构成一系列的
k
k
k维超矩形区域
k d kd kd树的每一个节点对应于一个 k k k维超矩形区域
构造kd树的方法如下:
(1)构造根节点,使根节点对应于k维空间中包含所有实例点的超矩形区域
(2)利用递归方法,不断对k维空间进行切分,生成子结点。在超矩形区域(结点)上选择一个坐标轴和其坐标轴上的一个切分点,确定一个超平面,该超平面通过选定的切分点并垂直于选定的坐标轴,将当前的超矩形区域切分为左右两个子区域;
(3)此时,实例被分到两个子区域;直至划分的子区域内没有实例
一般一次选择坐标轴对空间切分,切分点则为训练实例点在该坐标轴上的中位数,进而得到平衡kd树;
但平衡kd未必是最优的
算法:构造平衡kd树:
输入:
k k k维空间数据集 T = { x 1 , x 2 , . . . , x N } T=\{x_1,x_2,...,x_N\} T={x1,x2,...,xN},其中 x i = ( x i ( 1 ) , x i ( 2 ) , . . . , x i ( k ) ) T x_i = (x_i^{(1)},x_i^{(2)},...,x_i^{(k)})^{\mathrm{T}} xi=(xi(1),xi(2),...,xi(k))T
输出:kd树
(1)开始:构造根节点,对应包含 T T T的 k k k维空间的超矩形区域
选择 x ( 1 ) x^{(1)} x(1)为坐标轴,以 T T T中所有实例的 x ( 1 ) x^{(1)} x(1)坐标的中位数为切分点,将根节点对应的超矩形区域切分为两个子区域。切分由通过切分点并于坐标轴 x ( 1 ) x^{(1)} x(1)垂直的超平面实现.
由根节点生成深度为1的左、右字节点:左子节点对应坐标 x ( 1 ) x^{(1)} x(1)小于切分点的子区域,右子节点对应于坐标 x ( 1 ) x^{(1)} x(1)大于切分点的子区域。
降落在切分超平面上的实例点保存在根节点
(2)重复:对深度为 j j j的节点,选择 x ( l ) x^{(l)} x(l)为切分的坐标轴, l = j ( m o d k ) + 1 l = j(modk) + 1 l=j(modk)+1,以该节点的区域中所有实例的 x ( l ) x^{(l)} x(l)坐标的中位数为切分点,将该结点对应的超矩形区域切分为两个子区域。切分由通过切分点并与坐标轴 x ( l ) x^{(l)} x(l)垂直的超平面实现。
由该节点生成深度为j+1的左右子结点:左子节点对应坐标 x ( l ) x^{(l)} x(l)小于切分点的子区域,右子节点对应坐标 x ( l ) x^{(l)} x(l)大于切分点的子区域。
将落在切分超平面上的实例保存在该节点
(3)直到两个子区域没有实例存在时停止。形成 k d kd kd树
注意: l = j ( m o d k ) + 1 l = j(mod k) + 1 l=j(modk)+1 即用j来整除k,一般在由1到k的第一轮切分中,由于 j < k j<k j<k,使得实际 l = j + 1 l = j + 1 l=j+1,因此在重复阶段,就是依次遍历对每个特征下还未切分的节点进行切分
搜索kd树
算法:用kd树的最近邻搜索(也就是利用先前构造的平衡kd树来快速k近邻搜索)
输入:
已构造的 k d kd kd树,目标点 x x x;
输出:x的最近邻
(1)在kd树中找出包含目标点x的叶节点:从根节点出发,递归地向下访问kd树。若目标点x当前维的坐标小于切分点的坐标,则移动到左子节点,否则移动到右子节点。直到子节点为叶节点为止
(2)以此叶节点为“当前最近点”
(3)递归地向上回退,在每个节点进行以下操作:
(a)如果该节点保存的实例点比当前最近点距离目标点更近,则以该实例点为“当前最近点”
(b)当前最近点一定存在于该节点一个子节点对应的区域。检查该子节点的父节点的另一子节点对应的区域是否有更近的点。具体地,检查另一子节点对应的区域是否以目标点为求新、以目标点与“当前最近点”间的距离为半径的超球体相交。
如果相交,可能在另一个子节点对应的区域内存在距离目标点更近的点,移动到另一个子节点。接着,递归地进行最近邻搜索;
如果不相交,向上回退。
(4)当退回根节点时,搜索结束。最后的“当前最近点”即为 x x x的最近领点
习题
习题3.1
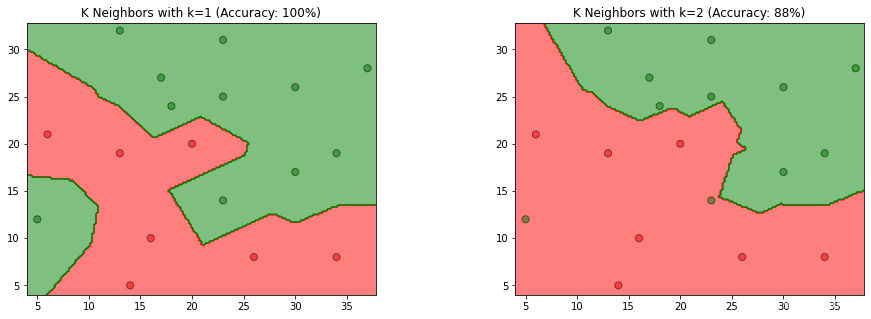
参照图3.1,在二维空间中给出实例点,画出 k k k为1和2时的 k k k近邻法构成的空间划分,并对其进行比较,体会 k k k值选择与模型复杂度及预测准确率的关系。
解答思路:
- 参照图3.1,使用已给的实例点,采用sklearn的KNeighborsClassifier分类器,对k=1和2时的模型进行训练
- 使用matplotlib的contourf和scatter,画出k为1和2时的k近邻法构成的空间划分
- 根据模型得到的预测结果,计算预测准确率,并设置图形标题
- 根据程序生成的图,比较k为1和2时,k值选择与模型复杂度、预测准确率的关系
解答步骤:
第1、2、3步:使用已给的实例点,对 k k k为1和2时的k近邻模型进行训练,并绘制空间划分
# Step1 导入需要用到的绘图、ML与numpy库
from matplotlib.colors import ListedColormap #matplotlib中的
import matplotlib.pyplot as plt
from sklearn.neighbors import KNeighborsClassifier #机器学习库中的KNN
import numpy as np #numpy
%matplotlib inline
# Step2 给出数据
data = np.array([[5, 12, 1],
[6, 21, 0],
[14, 5, 0],
[16, 10, 0],
[13, 19, 0],
[13, 32, 1],
[17, 27, 1],
[18, 24, 1],
[20, 20, 0],
[23, 14, 1],
[23, 25, 1],
[23, 31, 1],
[26, 8, 0],
[30, 17, 1],
[30, 26, 1],
[34, 8, 0],
[34, 19, 1],
[37, 28, 1]])
#Step 3 提取特征和分类类别
X_train = data[:,0:2]
Y_train = data[:,2]
#Step 4 对以给定的数据集,利用sklearn.neighbors中的KNeighborsClassifier分类起对k=1和k=2的模型训练
# KNeighborsClassifier? #此处用以学习该模型的若干参数
models = (KNeighborsClassifier(n_neighbors=1,n_jobs=-1),
KNeighborsClassifier(n_neighbors=2,n_jobs=-1))
# 参数介绍
# KNeighborsClassifier(
# n_neighbors=5, # Number of neighbors to use;default=5
# *,
# weights='uniform', # weight function used in prediction;default='uniform';还可以选'distance'
# algorithm='auto', # algorithm : {'auto', 'ball_tree', 'kd_tree', 'brute'}, default='auto'
# leaf_size=30,
# p=2, # Power parameter for the Minkowski metric;default=2 即确定距离度量的p取值
# metric='minkowski',
# metric_params=None,
# n_jobs=None, #default=None;``-1`` means using all processors
# **kwargs,
# )
# Step5 模型训练 利用嵌套表达式同时训练两个模型
models = (clf.fit(X_train,Y_train) for clf in models)
# Step6 绘图部分
## Step6.1 图像标题
titles = ('K Neighbors with k=1',
'K Neighbors with k=2')
## Step6.2 设置图像大小和图间距
fig = plt.figure(figsize=(15,5))
plt.subplots_adjust(wspace=0.4,hspace=0.4)
## Step6.3 提取绘图数据与数据边界
X0,X1 = X_train[:,0],X_train[:,1]
x_min, x_max = X0.min()-1, X0.max()+1
y_min, y_max = X1.min()-1, X1.max()+1
## Step6.4 构造网格点坐标矩阵
### 设置0.2的目的是生成更多的网格点,数值越小,划分空间之间的分隔线越清晰
xx, yy = np.meshgrid(np.arange(x_min,x_max,0.2),
np.arange(y_min,y_max,0.2))
# 语法:X,Y = numpy.meshgrid(x, y)
# 输入的x,y,就是网格点的横纵坐标列向量(非矩阵)
# 输出的X,Y,就是坐标矩阵。
print(xx)
print(xx.shape)
print('---')
print(yy)
## Step6.5 正式绘图
for clf, title, ax in zip(models,titles,fig.subplots(1,2).flatten()):
# 使用matplotlib的contourf和scatter,画出k为1和2时的k近邻法构成的空间划分
# 对所有网格点进行预测
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# 设置颜色列表
colors = ('red', 'green', 'lightgreen', 'gray', 'cyan')
# 根据类别数生成颜色
cmap = ListedColormap(colors[:len(np.unique(Z))])
# 绘制分隔线,contourf函数用于绘制等高线,alpha表示颜色的透明度,一般设置成0.5
ax.contourf(xx, yy, Z, cmap=cmap, alpha=0.5)
# 绘制样本点
ax.scatter(X0, X1, c=y_train, s=50, edgecolors='k', cmap=cmap, alpha=0.5)
# (3)根据模型得到的预测结果,计算预测准确率,并设置图形标题
# 计算预测准确率
acc = clf.score(X_train, y_train)
# 设置标题
ax.set_title(title + ' (Accuracy: %d%%)' % (acc * 100))
plt.show()
[[ 4. 4.2 4.4 ... 37.4 37.6 37.8]
[ 4. 4.2 4.4 ... 37.4 37.6 37.8]
[ 4. 4.2 4.4 ... 37.4 37.6 37.8]
...
[ 4. 4.2 4.4 ... 37.4 37.6 37.8]
[ 4. 4.2 4.4 ... 37.4 37.6 37.8]
[ 4. 4.2 4.4 ... 37.4 37.6 37.8]]
(145, 170)
---
[[ 4. 4. 4. ... 4. 4. 4. ]
[ 4.2 4.2 4.2 ... 4.2 4.2 4.2]
[ 4.4 4.4 4.4 ... 4.4 4.4 4.4]
...
[32.4 32.4 32.4 ... 32.4 32.4 32.4]
[32.6 32.6 32.6 ... 32.6 32.6 32.6]
[32.8 32.8 32.8 ... 32.8 32.8 32.8]]
补充知识:
np.meshgrid方法:用于构造网格点坐标矩阵,可参考https://blog.csdn.net/lllxxq141592654/article/details/81532855
第4步:比较 k k k为1和2时,k值选择与模型复杂度、预测准确率的关系
-
k
k
k值选择与模型复杂度的关系
根据书中第52页(3.2.3节: k k k值的选择)
如果选择较小的 k k k值,就相当于用较小的邻域中的训练实例进行预测,“学习”的近似误差会减小,只有与输入实例较近的(相似的)训练实例才会对预测结果起作用。 k k k值的减小就意味着整体模型变得复杂,容易发生过拟合。
如果选择较大的 k k k值,就相当于用较大邻域中的训练实例进行预测。 k k k值的增大就意味着整体的模型变得简单。
综上所属, k k k值越大,模型复杂度越低,模型越简单,容易发生欠拟合。反之, k k k值越小,模型越复杂,容易发生过拟合。
-
k
k
k值选择与预测准确率的关系
从图中观察到,当 k = 1 k=1 k=1时,模型易产生过拟合,当 k = 2 k=2 k=2时准确率仅有88%,故在过拟合发生前, k k k值越大,预测准确率越低,也反映模型泛化能力越差,模型简单。反之, k k k值越小,预测准确率越高,模型具有更好的泛化能力,模型复杂。
习题3.2
利用例题3.2构造的 k d kd kd树求点 x = ( 3 , 4.5 ) T x=(3,4.5)^T x=(3,4.5)T的最近邻点。
解答:
解答思路:
方法一:
- 使用sklearn的KDTree类,结合例题3.2构建平衡 k d kd kd树,配置相关参数(构建平衡树kd树算法,见书中第54页算法3.2内容);
- 使用tree.query方法,查找(3, 4.5)的最近邻点(搜索kd树算法,见书中第55页第3.3.2节内容);
- 根据第3步返回的参数,得到最近邻点。
方法二:
根据书中第56页算法3.3用
k
d
kd
kd树的最近邻搜索方法,查找(3, 4.5)的最近邻点
解答步骤:
方法一:
import numpy as np
from sklearn.neighbors import KDTree
# 构造数据
train_data = np.array([[2,3],
[5,4],
[9,6],
[4,7],
[8,1],
[7,2]])
# 1.利用sklearn.neighbors中的KDTree和train_data构造KDTree
## leaf_size = 2 表示设置平衡树
tree = KDTree(train_data,leaf_size=2)
# 2.使用tree.query方法来搜索最近邻
# dist表示与最近邻点的距离,ind表示最近邻点在train_data的位置
# test = tree.query(np.array([[3,4.5]]),k=1)
# list(test) # 此时可以观察到,tree.query(data,k=1) 返回距离和节点坐标
dist, ind = tree.query(np.array([[3,4.5]]),k=1)
dist
ind
node_index = ind[0]
node_index
# 3.获取最近邻点
x1 = train_data[node_index][0][0]
x2 = train_data[node_index][0][1]
print('x点(3,4.5)的最近邻点为({0},{1})'.format(x1,x2))
可得到点 x = ( 3 , 4.5 ) T x=(3,4.5)^T x=(3,4.5)T的最近邻点是 ( 2 , 3 ) T (2,3)^T (2,3)T
方法二:
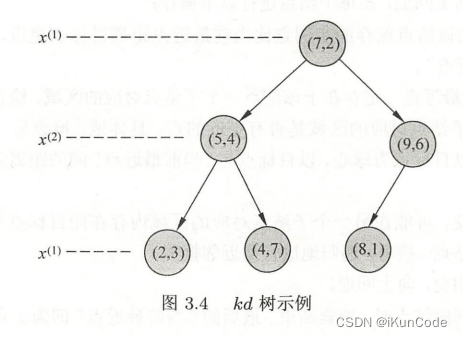
- 首先找到点 x = ( 3 , 4.5 ) T x=(3,4.5)^T x=(3,4.5)T所在领域的叶节点 x 1 = ( 4 , 7 ) T x_1=(4,7)^T x1=(4,7)T,则最近邻点一定在以 x x x为圆心, x x x到 x 1 x_1 x1距离为半径的圆内;
- 找到 x 1 x_1 x1的父节点 x 2 = ( 5 , 4 ) T x_2=(5,4)^T x2=(5,4)T, x 2 x_2 x2的另一子节点为 x 3 = ( 2 , 3 ) T x_3=(2,3)^T x3=(2,3)T,此时 x 3 x_3 x3在圆内,故 x 3 x_3 x3为最新的最近邻点,并形成以 x x x为圆心,以 x x x到 x 3 x_3 x3距离为半径的圆;
- 继续探索 x 2 x_2 x2的父节点 x 4 = ( 7 , 2 ) T x_4=(7,2)^T x4=(7,2)T, x 4 x_4 x4的另一个子节点 ( 9 , 6 ) (9,6) (9,6)对应的区域不与圆相交,故不存在最近邻点,所以最近邻点为 x 3 = ( 2 , 3 ) T x_3=(2,3)^T x3=(2,3)T。
可得到点 x = ( 3 , 4.5 ) T x=(3,4.5)^T x=(3,4.5)T的最近邻点是 ( 2 , 3 ) T (2,3)^T (2,3)T
**习题3.3(需要有数据结构中关于树的基础知识)
参照算法3.3,写出输出为 x x x的 k k k近邻的算法。
解答:
解答思路:
- 参考书中第56页算法3.3(用 k d kd kd树的最近邻搜索),写出输出为 x x x的 k k k近邻算法;
- 根据算法步骤,写出算法代码,并用习题3.2的解进行验证。
解答步骤:
第1步:用 k d kd kd树的 k k k邻近搜索算法
根据书中第56页算法3.3(用 k d kd kd树的最近邻搜索)
输入:已构造的kd树;目标点 x x x;
输出: x x x的k近邻
(1)在 k d kd kd树中找出包含目标点 x x x的叶结点:从根结点出发,递归地向下访问树。若目标点 x x x当前维的坐标小于切分点的坐标,则移动到左子结点,否则移动到右子结点,直到子结点为叶结点为止;
(2)如果“当前 k k k近邻点集”元素数量小于 k k k或者叶节点距离小于“当前 k k k近邻点集”中最远点距离,那么将叶节点插入“当前k近邻点集”;
(3)递归地向上回退,在每个结点进行以下操作:
(a)如果“当前 k k k近邻点集”元素数量小于 k k k或者当前节点距离小于“当前 k k k近邻点集”中最远点距离,那么将该节点插入“当前 k k k近邻点集”。
(b)检查另一子结点对应的区域是否与以目标点为球心、以目标点与“当前 k k k近邻点集”中最远点间的距离为半径的超球体相交。
如果相交,可能在另一个子结点对应的区域内存在距目标点更近的点,移动到另一个子结点,接着,递归地进行近邻搜索;
如果不相交,向上回退;
(4)当回退到根结点时,搜索结束,最后的“当前 k k k近邻点集”即为 x x x的近邻点。
第2步:根据算法步骤,写出算法代码,并用习题3.2的解进行验证
import json
class Node:
"""节点类"""
def __init__(self, value, index, left_child, right_child):
self.value = value.tolist()
self.index = index
self.left_child = left_child
self.right_child = right_child
def __repr__(self):
return json.dumps(self, indent=3, default=lambda obj: obj.__dict__, ensure_ascii=False, allow_nan=False)
class KDTree:
"""kd tree类"""
def __init__(self, data):
# 数据集
self.data = np.asarray(data)
# kd树
self.kd_tree = None
# 创建平衡kd树
self._create_kd_tree(data)
def _split_sub_tree(self, data, depth=0):
# 算法3.2第3步:直到子区域没有实例存在时停止
if len(data) == 0:
return None
# 算法3.2第2步:选择切分坐标轴, 从0开始(书中是从1开始)
l = depth % data.shape[1]
# 对数据进行排序
data = data[data[:, l].argsort()]
# 算法3.2第1步:将所有实例坐标的中位数作为切分点
median_index = data.shape[0] // 2
# 获取结点在数据集中的位置
node_index = [i for i, v in enumerate(
self.data) if list(v) == list(data[median_index])]
return Node(
# 本结点
value=data[median_index],
# 本结点在数据集中的位置
index=node_index[0],
# 左子结点
left_child=self._split_sub_tree(data[:median_index], depth + 1),
# 右子结点
right_child=self._split_sub_tree(
data[median_index + 1:], depth + 1)
)
def _create_kd_tree(self, X):
self.kd_tree = self._split_sub_tree(X)
def query(self, data, k=1):
data = np.asarray(data)
hits = self._search(data, self.kd_tree, k=k, k_neighbor_sets=list())
dd = np.array([hit[0] for hit in hits])
ii = np.array([hit[1] for hit in hits])
return dd, ii
def __repr__(self):
return str(self.kd_tree)
@staticmethod
def _cal_node_distance(node1, node2):
"""计算两个结点之间的距离"""
return np.sqrt(np.sum(np.square(node1 - node2)))
def _search(self, point, tree=None, k=1, k_neighbor_sets=None, depth=0):
n = point.shape[1]
if k_neighbor_sets is None:
k_neighbor_sets = []
if tree is None:
return k_neighbor_sets
# (1)找到包含目标点x的叶结点
if tree.left_child is None and tree.right_child is None:
# 更新当前k近邻点集
return self._update_k_neighbor_sets(k_neighbor_sets, k, tree, point)
# 递归地向下访问kd树
if point[0][depth % n] < tree.value[depth % n]:
direct = 'left'
next_branch = tree.left_child
else:
direct = 'right'
next_branch = tree.right_child
if next_branch is not None:
# (3)(b)检查另一子结点对应的区域是否相交
k_neighbor_sets = self._search(point, tree=next_branch, k=k, depth=depth + 1,
k_neighbor_sets=k_neighbor_sets)
# 计算目标点与切分点形成的分割超平面的距离
temp_dist = abs(tree.value[depth % n] - point[0][depth % n])
if direct == 'left':
# 判断超球体是否与超平面相交
if not (k_neighbor_sets[0][0] < temp_dist and len(k_neighbor_sets) == k):
# 如果相交,递归地进行近邻搜索
# (3)(a) 判断当前结点,并更新当前k近邻点集
k_neighbor_sets = self._update_k_neighbor_sets(k_neighbor_sets, k, tree, point)
return self._search(point, tree=tree.right_child, k=k, depth=depth + 1,
k_neighbor_sets=k_neighbor_sets)
else:
# 判断超球体是否与超平面相交
if not (k_neighbor_sets[0][0] < temp_dist and len(k_neighbor_sets) == k):
# 如果相交,递归地进行近邻搜索
# (3)(a) 判断当前结点,并更新当前k近邻点集
k_neighbor_sets = self._update_k_neighbor_sets(k_neighbor_sets, k, tree, point)
return self._search(point, tree=tree.left_child, k=k, depth=depth + 1,
k_neighbor_sets=k_neighbor_sets)
else:
return self._update_k_neighbor_sets(k_neighbor_sets, k, tree, point)
return k_neighbor_sets
def _update_k_neighbor_sets(self, best, k, tree, point):
# 计算目标点与当前结点的距离
node_distance = self._cal_node_distance(point, tree.value)
if len(best) == 0:
best.append((node_distance, tree.index, tree.value))
elif len(best) < k:
# 如果“当前k近邻点集”元素数量小于k
self._insert_k_neighbor_sets(best, tree, node_distance)
else:
# 叶节点距离小于“当前 𝑘 近邻点集”中最远点距离
if best[0][0] > node_distance:
best = best[1:]
self._insert_k_neighbor_sets(best, tree, node_distance)
return best
@staticmethod
def _insert_k_neighbor_sets(best, tree, node_distance):
"""将距离最远的结点排在前面"""
n = len(best)
for i, item in enumerate(best):
if item[0] < node_distance:
# 将距离最远的结点插入到前面
best.insert(i, (node_distance, tree.index, tree.value))
break
if len(best) == n:
best.append((node_distance, tree.index, tree.value))
# 打印信息
def print_k_neighbor_sets(k, ii, dd):
if k == 1:
text = "x点的最近邻点是"
else:
text = "x点的%d个近邻点是" % k
for i, index in enumerate(ii):
res = X_train[index]
if i == 0:
text += str(tuple(res))
else:
text += ", " + str(tuple(res))
if k == 1:
text += ",距离是"
else:
text += ",距离分别是"
for i, dist in enumerate(dd):
if i == 0:
text += "%.4f" % dist
else:
text += ", %.4f" % dist
print(text)
import numpy as np
X_train = np.array([[2, 3],
[5, 4],
[9, 6],
[4, 7],
[8, 1],
[7, 2]])
kd_tree = KDTree(X_train)
# 设置k值
k = 1
# 查找邻近的结点
dists, indices = kd_tree.query(np.array([[3, 4.5]]), k=k)
# 打印邻近结点
print_k_neighbor_sets(k, indices, dists)
x点的最近邻点是(2, 3),距离是1.8028
# 打印kd树
kd_tree
{
"value": [
7,
2
],
"index": 5,
"left_child": {
"value": [
5,
4
],
"index": 1,
"left_child": {
"value": [
2,
3
],
"index": 0,
"left_child": null,
"right_child": null
},
"right_child": {
"value": [
4,
7
],
"index": 3,
"left_child": null,
"right_child": null
}
},
"right_child": {
"value": [
9,
6
],
"index": 2,
"left_child": {
"value": [
8,
1
],
"index": 4,
"left_child": null,
"right_child": null
},
"right_child": null
}
}
上述打印的平衡kd树和书中第55页的图3.4 kd树示例一致。
更换数据集,使用更高维度的数据,并设置 k = 3 k=3 k=3
import numpy as np
X_train = np.array([[2, 3, 4],
[5, 4, 4],
[9, 6, 4],
[4, 7, 4],
[8, 1, 4],
[7, 2, 4]])
kd_tree = KDTree(X_train)
# 设置k值
k = 3
# 查找邻近的结点
dists, indices = kd_tree.query(np.array([[3, 4.5, 4]]), k=k)
# 打印邻近结点
print_k_neighbor_sets(k, indices, dists)
输出:
x点的3个近邻点是(4, 7, 4), (5, 4, 4), (2, 3, 4),距离分别是2.6926, 2.0616, 1.8028





















 7545
7545











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








