之前两篇blog介绍了等式约束最优化,不等式约束最优化的最优性条件。
(http://blog.csdn.net/ice110956/article/details/17557795
http://blog.csdn.net/ice110956/article/details/17562429)
了解最优性条件后,我们通过最优性条件的性质可以来求解,或者验证最优解。通常会构造一个拉格朗日乘子,求导构造得到最优性条件的形式来求解。
回顾下最优化问题的三个基本形式:

无约束问题
可以通过微积分的知识直接求解。
等式约束问题
我们可以构造拉格朗日乘子后直接求解,也就是拉格朗日乘子法。如下:
我们可以定义如下的n+l元函数:
称为lagrange函数。也就是把目标函数与约束函数写在一起求解,并用向量的形式来表示。
上式分别对x与lamda求导为零求解后,即为可能极值点。(证明可见开头两篇blog)
不过上述的点可能是鞍点,也可能是极值点,具体判断要用二阶充分条件。
*补充,解析法求导,可以求得拉格朗日函数可能极值点。但是,经证明,拉格朗日函数没有最小值,也就是通过序列迭代法不能得到解。这时候就要用到乘子+罚函数的方法。
不等式约束问题
上一篇blog我们得到不等式约束的最优性条件是KKT条件,如下:
上式的第一个式子,我们也可以写成这样的式子:
然后求导,也就是拉格朗日乘子。(证明可见开头两篇blog)
上式虽然我们得出了KKT条件,但是还是解不了的,因为第二个式子理解为lambda=0或者ci(x)=0;也就是单独使用最优性条件无法直接解出不等式约束的最优解。我们只能通过KKT条件来验证某个解是否是最优解。
不过,前一篇blog中(http://blog.csdn.net/ice110956/article/details/17631765 )提到的外罚函数和内罚函数,把不等式约束问题转化为等式约束问题。然后,我们再通过拉格朗日乘子法来求解等式问题。也就是说,通过罚函数+乘子法,我们可迭代求解不等式约束问题。
小结
通过构造拉格朗日乘子,我们可以解等式约束问题,验证但不可求解不等式约束问题。








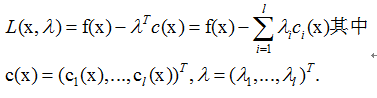















 1538
1538

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








