所谓的最优性条件就是最优解的性质。
我们通过最优性条件的研究,能够对于优化的步骤,以及迭代求解时的结束条件有很大帮助。
最优化问题常见的有无约束优化,等式约束优化,不等式约束优化。这里用两篇blog分别讨论等式约束优化与不等式约束最优化的最优性条件。
我们首先讨论等式约束的情况下,其最优解满足怎样的性质。
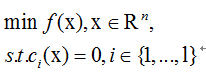
三维空间:
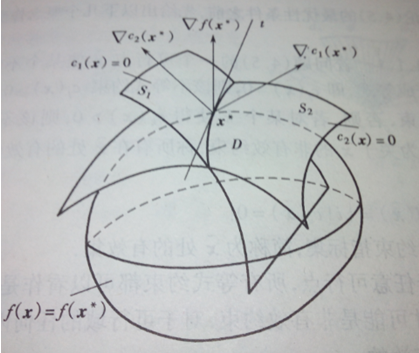
以下以三维空间为特例,看看最优解有哪些性质。
如上图,X为局部最优解,那么其必在S1与S2的交线D(及可行域)上,并且目标函数与约束函数的 梯度 共面。如果不共面,那么f(x)梯度向可行域D上的投影不为零。于是沿着这个投影移动,可使得目标函数下降,也就不是最优解。
根据共面的条件,我们可以推出:
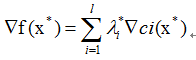
也就是三维空间的最优性条件。
等式约束一阶必要条件:
上述是三维空间上的特殊情况,对于等式约束的一般情况,我们可以通过微积分,来得到关于导函数的一些性质。下面直接写出其完整性质。
一阶必要条件:
上式为必要条件,不是充分条件。
具体解法:
我们可以定义如下的n+l元函数:
称为lagrange函数。也就是把目标函数与约束函数写在一起求解,并用向量的形式来表示。
上式分别对x与lamda求导为零求解后,即为可能极值点。
不过上述的点可能是鞍点,也可能是极值点,具体判断要用到如下的二阶充分条件。
*补充:我们使上面的拉格朗日乘子为0,可以求得可能极值点。不过如果采用序列迭代法,经证明,上面的函数没有最小值,也就是使用序列迭代法得不到解。
二阶充分条件:
在满足一阶必要条件的前提下,我们现在要判断所得的可能极值点到底是不是极值点,就要用到二阶充分判断条件:
若 函数关于x的Hesse矩阵在约束超曲面的切平面上正定,则x就是严格局部极小点。
Hesse矩阵的知识:
在数学中,海森矩阵(Hessian matrix或Hessian)是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵,此函数如下:
如果f所有的二阶导数都存在,那么f的海森矩阵即:
其中 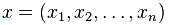
小结:等式最优化问题,把约束条件与目标函数写在一起,称为langrang函数,对X,lamda求导取零后,在通过二阶的hesse矩阵是否正定来进一步判断。








 本文探讨了等式约束最优化问题中的最优性条件,包括一阶必要条件与二阶充分条件,并介绍了拉格朗日乘子法的应用。
本文探讨了等式约束最优化问题中的最优性条件,包括一阶必要条件与二阶充分条件,并介绍了拉格朗日乘子法的应用。

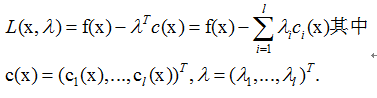
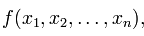
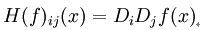

















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








