OpenGL中六种常见坐标系:
1. Object or model coordinates(模型坐标系)
2. World coordinates(世界坐标系)
3. Eye (or Camera) coordinates(视坐标系)
4. Clip coordinates(裁剪坐标系)
5. Normalized device coordinates(归一化设备坐标系)
6. Window (or screen) coordinates(屏幕坐标系)
当然这六中坐标系只是经常在开发中涉及的,还有其他很多坐标系,比如在进行法向贴图的时候的切向坐标系等,此处只介绍这六中坐标系。
需要注意的是模型坐标系、世界坐标系、视坐标系以及裁剪坐标系任何时候都是右手坐标系。默认情况下这四个坐标系完全重合,默认这四个坐标系的原点都在屏幕中心,从原点向右为x轴正半轴,从原点向上为y轴正半轴,从原点垂直于屏幕向外是z轴的正半轴。如果进行了某些矩阵操作变换,那么这四个坐标系就很可能不在重合,不过这四个坐标系还是右手坐标系。NDC坐标系(归一化设备坐标系)是左手坐标系,其z轴方向与前四个坐标系的z轴方向相反。
Object or model coordinates(模型坐标系)
所谓的模型指的就是一个三维的物体。每个物体都有其自身的模型坐标系,也就是说物体A的模型坐标系为Coordinate System A,物体B的模型坐标系为Coordinate System B,二者的模型坐标系不同。模型坐标系是一个假想的坐标系,该坐标系与物体的相对位置始终是不变的。在进行了glLoadIdentity()之后,模型坐标系和世界坐标系是重合的,但是如果调用了glTranslate()或者glRotate(),模型坐标系就会进行相应的平移和旋转。该坐标系以物体的中心为坐标原点,物体的旋转、平移等操作都是以模型坐标系进行的。这时当物体模型进行旋 转、平移等操作时,模型坐标系也执行相应的旋转、平移等操作。在OpenGL中绘图时,都是首先通过glTranslate、glRotate等来改变模型坐标系与世界坐标系的相对位置,然后在模型坐标系中用glVertexf等绘图,比如绘 制了一个点glVertexf(1,2,3),那么坐标(1,2,3)是模型坐标系中的坐标,而不是世界坐标系中的坐标。
World coordinates(世界坐标系)
这个坐标系就是我们生活的真实的3D场景,在OpenGL中有且只有一个世界坐标系。模型坐标系中的模型坐标左乘模型矩阵之后会转化为世界坐标,假设模型坐标系中有一点P,其坐标为Pmodel(Xmodel,Ymodel,Zmodel),该点左乘模型矩阵Mmodel之后就会得到该点在世界坐标系中的坐标Pworld(Xworld,Yworld,Zworld),即
上式中的Mmodel就是模型矩阵,是一个4×4的矩阵组成如下图所示,

上式中的m3,m7,m11均为0,m15为1。 (m12,m13,m14)可以表示一个点P,P点表示的是物体的模型坐标系的坐标原点在世界坐标系中的位置。剩下的9个值可分为三组(m0,m1,m2)、(m4,m5,m6)、(m8,m9,m10),这三组可表示三个向量vector1、vector2、vector3,而且这三个向量都是归一化向量,也就是说向量长度为1。其中vector1表示的是物体的模型坐标系的x轴正半轴在世界坐标系中的方向,vector2表示的是物体的模型坐标系的y轴的正半轴在世界坐标系中的方向,vector3表示的是物体的模型坐标系的z轴正半轴在世界坐标系中的方向。由此可以看出模型矩阵包含了所有模型坐标系的信息(模型坐标系的原点在世界坐标系中的位置以及模型坐标系的三个坐标轴在世界坐标系中的方向)。由于模型坐标系的三个坐标轴互相两两垂直,所以vector1、vector2、vector3互相垂直。那么根据数学定义由其中任意两个向量相互叉乘即可得到另一个向量,即有如下三个关系式:
vector1 叉乘 vector2 = vector3;
vector2 叉乘 vector3 = vector1;
vector3 叉乘 vector1 = vector2;
又因为vector1、vector2和vector3都是单位向量,那么可知:
m0*m0 + m1*m1 + m2*m2 = 1;
m4*m4 + m5*m5 + m6*m6 = 1;
m8*m8 + m9*m9 + m10*m10 = 1;
根据上述理论,假设我们已知物体的模型坐标的原点在世界坐标系中的坐标为P,物体的模型坐标系的x、y、z三个坐标轴的正半轴在世界坐标系中的方向分别为vector1、vector2、vector3,且这三个向量都是归一化向量。那么根据这些信息我们就直接可以写出物体的模型矩阵,如下所示:

Eye (or Camera) coordinates(视坐标系)
我们绘制的图形最终要呈现在视坐标系中,视坐标系是右手坐标系的。那么什么是视坐标系呢?视坐标系就是Camera坐标系。现在打个比 方,你站在世界坐标系中,你的眼睛就是Camera,你的眼睛平视前方,并且保持视线方向与头顶的朝向互相垂直。现在你的眼睛就是视坐标系的坐标原点,你的视线方向就是视坐标系Z轴的负半轴方向,你的头顶的朝向就是视坐标系的Y轴正半轴方向,与YOZ相互垂直向右的指向就是X轴正半轴的方向,X轴正半轴可由Y与Z叉乘得到,Camera的视坐标系也可以称为uvn坐标系,对应着世界坐标系的XYZ三个轴。默认情况下,视坐标系与世界坐标系是重合的。需要注意的是Camera本身就是一种普通的物体,即Camera就是一种模型,自然就有了前面所述的模型坐标系。不过Camera又是一种有点特殊的模型,为什么这么说呢?因为正常的模型都会在三维空间中画出来,但是一般情况下我们不会在三维空间中把Camera画出来(当然也可以将其在3D空间中画出来),所以一般情况下我们可以把Camera看作是透明的模型,但是上述模型坐标系的一系列理论都适用于Camera。 我们在开头就说了每次点从某个坐标系变换到另一个坐标系的时候都要左乘某个变换矩阵,从世界坐标系变换到视坐标系的时候所要左乘的变换矩阵我们称之为视点矩阵,需要特别注意的是视坐标系并不神秘,其实视坐标系就是Camera的模型坐标系。在一般情况下,3D空间中只有一个Camera,那么也就是只有一个视坐标系,视坐标系就是Camera的模型坐标系。既然视坐标系就是Camera的模型坐标系,那么视坐标系中某点Pview(Xview,Yview,Zview)就是Camera的模型坐标系中点Pcamera_model(Xcamera_model,Ycamera_model,Zcamera_model),即

世界坐标系中的点左乘视点矩阵即可得到视点坐标系中坐标,那么有如下定义:

当然又因为Pview就是Pcamera_model,所以也有如下定义:

那么视点矩阵Mview如何计算呢?
我们上面说过Camera也是一种模型,其自身也有模型坐标系,假设我们已知Camera的模型坐标系的原点在世界坐标系中的坐标以及Camera的模型坐标系的三个坐标轴的正半轴在世界坐标系中的方向,那么我们就知道了Camera的模型矩阵Mmodel。
我们已知将世界坐标系中的点转换到视坐标系中时有如下定义:
Pview = Mview•Pworld,
我们又根据模型坐标系中的点转换到世界坐标系中的定义得知:
Pworld = Mcamera_model•Pcamera_model,所以将Pworld的值带入上式得
Pview = Mview•Pworld = Mview•(Mcamera_model•Pcamera_model) = (Mview•Mcamera_model)•Pcamera_model
即Pview = (Mview•Mcamera_model) •Pcamera_model,又已知Pview = Pcamra_model,那么则得到
Pcamera_model = (Mview•Mcamera_model) •Pcamera_model,所以(Mview•Mcamera_model)为单位矩阵,也就是说Mview与Mcamera_model互为逆矩阵,所以
现在视点矩阵就计算完了,就是Camera的模型矩阵的逆矩阵。
现在大家可以回想一下OpenGL中常用的glLookAt(cameraPoint,targetPoint,upDirection)方法,该方法用于设置camera,其中cameraPoint是摄像机在世界坐标系中位置,targetPoint是摄像机观察的世界坐标系中的某点,upDirection指的是摄像机的头顶朝向在世界坐标系中的方向。我们可以根据这三个参数完全推算出camera的模型矩阵,计算过程如下:

摄像机的模型矩阵由以上16个数据组成,根据我们之前所述,m3、m7、m11都为0,m15为1。我们根据cameraPoint可以得知m12=cameraPoint.x, m13= cameraPoint.y, m14= cameraPoint.z,我们根据targetPoint和cameraPoint这两个点就能得到camera的视线方向,视线方向的反方向就是Camera的模型坐标系的z轴正半轴在世界坐标系中的方向,假设该方向的归一化向量是vector3,那么m8=vector3.x, m9=vector3.y, m10=vector3.z。upDirection就是Camera的模型坐标系的y轴正半轴在世界坐标系中的方向,假设该方向的归一化向量是vector2,那么m4=vector2.x, m5=vector2.y, m6=vector2.z。由于三个坐标轴互相垂直,那么Camera的模型坐标系的x轴正半轴在世界坐标系中的归一化后的方向vector1 = vector2叉乘 vector3。则m0=vector1.x, m1=vector1.y, m2=vector1.z。这样我们根据glLookAt(cameraPoint,targetPoint,upDirection)中的三个参数完全推出了Camera的模型矩阵,同时我们便可以计算出视点矩阵Mview为Camera模型矩阵的逆矩阵。也就是说glLookAt方法确定了Camera的模型矩阵,而且确定了3D空间的视点矩阵。
Clip coordinates(裁剪坐标系)
现实生活中的场景都满足“近大远小”的特点,但是视点坐标系中并不满足“近大远小”的特点,视点坐标系中的物体远近都一样大,为了将上一步得到的视点坐标转换为符合“近大远小”特点的坐标,我们需要将视点坐标左乘一个变换矩阵,我们称这个矩阵为投影矩阵,相乘得到的坐标称为投影坐标,但一般情况下我们更多地称其为裁剪坐标(为什么叫这个名字下面会解释)。Pclip = Mproj•Pview。裁剪坐标系也是右手坐标系。
首先我们会定义一个视景体,位于视景体内的物体我们才会看到,不在视景体内的物体就会被裁剪抛弃掉。视景体如下所示:

视景体是由六个参数构成的: left、right、top、bottom以及near和far。视景体是存在于视坐标系中的,这6个参数也是视坐标系中的。near表示的是视坐标系的坐标原点近裁剪面的距离,far表示的是视坐标系的坐标原点到远裁剪面的距离。[left,right]对应近裁剪面的x的值域,[bottom,top]对应近裁剪面的y的值域,一般情况下left=-right、bottom=-top。根据这六个参数就可以构造投影矩阵了。此处我们暂时不讨论如何构建该矩阵。
在GLSL的顶点着色器中,我们一般都要计算设置gl_Position的值。一般情况下该值这样设置: gl_Position = uPMatrix * uMVMatrix * vec4(aVertexPosition,1.0);
其中aVertexPosition为模型坐标,uMVMatrix为模型视点矩阵,即为视点矩阵与模型矩阵的乘积,则uMVMatrix = uViewMatrix * uModelMatrix。uPMatrix是投影矩阵,gl_Position就是经过了投影的裁剪坐标,也就是说gl_Position所在的坐标系就是投影坐标系。现在我们来解释一下这个坐标系为什么叫做“裁剪坐标系”,看看哪里来的“裁剪”二字:
需要特别注意的是,模型坐标系、世界坐标系、视点坐标系中的第四个分量w都是1,但是经过了投影变换之后的坐标的w分量不再为1,这时候就可以发挥w分量的作用了。在我们手动编程计算完gl_Position之后,进入GPU自身的流水管线,GPU会根据裁剪坐标gl_Position中xyz分量与w分量绝对值的大小进行比较进行裁剪。具体的过程是:GPU依次将gl_Position中x、y、z的绝对值与w的绝对值分别比较,只要有一个分量的绝对值大于w的绝对值,GPU就认为该点不在视景体内,就会被裁减掉,也就是说裁剪的过程是GPU自己进行的,没有被裁减掉的坐标xyz分量的绝对值都小于w的绝对值。所以现在应该知道经过投影之后的坐标是为了让GPU进行裁剪用的,所以才叫做“裁剪坐标”。
Normalized device coordinates(归一化设备坐标系)
裁剪坐标在经过GPU自动的裁剪之后会过滤掉那些位于视景体之外的坐标,只保留位于视景体内的坐标,然后GPU会自动进行投影除法(projective division)。

具体的过程是:会将齐次坐标转换为普通的三元的坐标(只有xyz,无w),会让裁剪坐标(裁剪坐标也是齐次坐标,包含w信息)中的xyz依次除以w,得到新的xyz,新的xyz就是归一化后的坐标,即归一化设备坐标(Normalized Device Coordinates),NDC坐标存放于一个边长为2的立方体坐标系中,NDC坐标是三分量的坐标,只包含xyz信息,不再包含w信息。归一化后的NDC坐标中的x、y、z的取值范围都是[-1,1]。x、y的取值范围是[-1,1],所表达的含义是将屏幕的中心点对应于[0,0],屏幕左下点对应[-1,-1],屏幕右上点对应于[1,1],x和y能够表示出该点相对于屏幕中心原点的位置。NDC坐标中的z表示了深度信息,取值范围也是[-1,1]。
需要特别注意的是NDC坐标系与裁剪坐标系相比其Z轴方向发生了翻转,也就是说NDC坐标系是左手坐标系,这个非常重要。而且其xyz的取值都是[-1,1]。Xndc与Yndc比较好计算,就是简单的线性比例计算而已。那么Zndc如何计算呢?
Zndc表示的是深度信息,视景体的近裁剪面的Zndc为-1,视景体的远裁剪面的Zndc为1。Zndc与Zview并不是线性的关系,两者的具体关系是:

其中far指的是视坐标系中坐标原点到远裁剪面的距离,near指的是视坐标系中坐标原点到近裁剪面的距离,Zveiw是视坐标系中的Z值。这样就可以根据Zview计算出Zndc。
当位于近裁剪面时,Zview=-near,则计算出的Zndc=-1;
当位于远裁剪面时,Zview=-far,则计算出的Zndc=1。
那么Zview为何值时,Zndc为0呢?注意肯定不是近裁剪面与远裁剪面的中间点。
根据上面的公式我们可以计算出当Zndc=0时,

Window (or screen) coordinates(屏幕坐标系)
最后系统需要根据NDC坐标将其画到我们的屏幕上,此处不再通过矩阵来完成了,而是通过调用命令glViewPort(x, y, width, height)。
x、y指定了视口矩形的左上角点,默认值是(0,0);
width、height指定了视口的宽度和高度。当OpenGL上下文第一次绑定到window时,width和height被默认设置为window的宽度和高度。
glViewport指定了x、y从NDC坐标系(归一化设备坐标系)到屏幕坐标系的仿射变换。如果(Xndc,Yndc)是归一化坐标,那么屏幕坐标(Xwindow,Ywindow)计算如下:

一般情况下,在调用glViewPort时,我们一般使用glViewPort(0, 0, width, height),也就是前两个偏移坐标都为0,所以上式简化为:

在片源着色器中有一个内建的输入vec4变量gl_FragCoord,gl_FragCoord表示的是片元的坐标位置,包含了片元的窗口相对坐标值(x, y, z, 1/w)
其中此处的gl_FragCoord.x和gl_FragCoord.y分别就是上述计算的Xwindow和Ywindow,即表示相对于屏幕左上角的屏幕坐标位置。屏幕坐标系的左上角为坐标原点,向右为X轴正半轴,向下为Y轴正半轴。gl_FragCoord.z表示的是片元的深度值,默认情况下,在片源着色器中gl_FragCoord.z的深度取值范围是[0, 1],注意,NDC坐标系中的z的取值范围是[-1, 1],z值的坐标范围之所以能从NDC坐标系中的[-1,1]转变到屏幕坐标系中的[0, 1],是因为OpenGL会根据函数glDepthRange(nearVal, farVal)中nearVal与farVal的值,将NDC坐标系中z从[-1, 1]映射到[nearVal, farVal],这一映射就是简单地线性变换。其中,如果没有主动调用过glDepthRange,那么OpenGL就认为nearVal就是0,farVal就是1。 在NDC坐标系中,近裁剪面的z值为-1,远裁剪面的z值为1,根据nearVal与farVal,将近、远裁剪面的z值分别映射到了nearVal与farVal,默认情况下在屏幕坐标系中,原近裁剪面的深度z就变成了0,原远裁剪面的深度z就变成了1。 gl_FragCoord中的第四个分量是存储了“投影除法”的相关信息1/w。
至此我们就完成了将一个模型坐标转换成屏幕坐标的一系列变换。











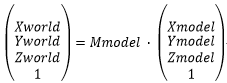
















 5118
5118

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








