2020-12-30 activiz空间位置变换以及圆柱空间参数方程

1. vtkTransform
activiz中actor位置，除了自身的属性，比如setposition之类的之外，也可以应用vtkTransform。左乘和右乘是不一样的。
需要注意的是：setposition只是改变了物体的显示位置而不是实际位置，而Translate改变的是实际位置，如果实际位置离原点太远，会出现显示不稳定的问题，比如颤动。

vtkTransform cubetransform_dir = vtkTransform.New();// 空间变换对象
cubetransform_dir.PostMultiply();  // 设置右乘变换矩阵
cubetransform_dir.RotateX(90);  // 绕x轴旋转 单位是° 有四种旋转方式
cubetransform_dir.Translate(x, y, z);	//平移 cubeActor.SetUserTransform(cubetransform_dir); // 柱体空间变换 

2. vtkTransform在圆柱表示的应用
已知圆柱的倾角（与铅垂线的锐角），倾向（以X轴正向顺时针旋转），中心坐标，表示其位置。由于采用activiz中内置的vtkCylinderSource生成圆柱，所以生成的都是轴线沿着Y轴正向的，需要旋转。

transform_dir.RotateX(90); // 绕x轴旋转 单位是° 本行为主轴线为Y+时采用，若主轴为Z+ 不需要该旋转
transform_dir.RotateY(b.slopeRatio); //倾角
transform_dir.RotateZ(b.trend); //倾向
//x,y,z为桩中心坐标（一半桩长处）
transform_dir.Translate(x, y, z);
pileActor.SetUserTransform(transform_dir);                   

3. 圆柱空间参数方程
相对铅垂线倾斜：

垂直水平面：

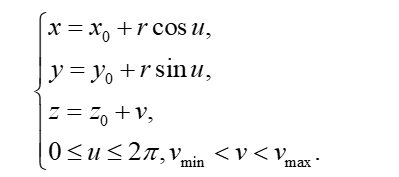
式中：x0,y0,z0为底面中心。A、B、C为轴线直线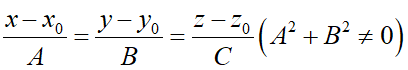
的参数。