Wigner distribution function
The Wigner distribution function (WDF) was first proposed in physics to account for quantum corrections to classical statistical mechanics in 1932 by Eugene Wigner, cf. Wigner quasi-probability distribution.
Given the shared algebraic structure between position-momentum and time-frequency pairs, it may also usefully serve in signal processing, as a transform in time-frequency analysis. Compared to a short-time Fourier transform, such as the Gabor transform, the Wigner distribution function can furnish higher clarity in some cases.
Contents[hide] |
[edit]Mathematical definition
There are several different definitions for the Wigner distribution function. The definition given here is specific to time-frequency analysis. The Wigner distribution function 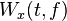 is
is
where 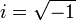 is the imaginary unit. The WDF is essentially the Fourier transform of the input signal’s autocorrelation function — the Fourier spectrum of the product between the signal and its delayed, time reversed copy, as a function of the delay.
is the imaginary unit. The WDF is essentially the Fourier transform of the input signal’s autocorrelation function — the Fourier spectrum of the product between the signal and its delayed, time reversed copy, as a function of the delay.
[edit]Time-frequency analysis example
Here are some examples illustrating how the WDF is used in time-frequency analysis.
[edit]Constant input signal
When the input signal is constant, its time-frequency distribution is a horizontal line along the time axis. For example, if x(t) = 1, then
[edit]Sinusoidal input signal
When the input signal is a sinusoidal function, its time-frequency distribution is a horizontal line parallel to the time axis, displaced from it by the sinusoidal frequency. For example, if  , then
, then
[edit]Chirp input signal
When the input signal is a chirp function, the instantaneous frequency is a linear function. This means that the time frequency distribution should be a straight line. For example, if 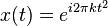 , then its instantaneous frequency is
, then its instantaneous frequency is 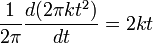 , and by WDF
, and by WDF
[edit]Delta input signal
When the input signal is a delta function, since it is only non-zero at t=0 and contains infinite frequency components, its time-frequency distribution should be a vertical line across the origin. This means that the time frequency distribution of the delta function should also be a delta function. By WDF
The Wigner distribution function is best suited for time-frequency analysis when the input signal's phase is 2nd order or lower. For those signals, WDF can exactly generate the time frequency distribution of the input signal.
[edit]Performance of Wigner distribution function
Here are some examples to show performance features of the Wigner distribution function preferable to the Gabor transform.
 rectangular function
rectangular function
[edit]Cross term property
The Wigner distribution function is not a linear transform. A cross term ("time beats") occurs when there is more than one component in the input signal, analogous in time to frequency beats. In the ancestral physics Wigner quasi-probability distribution, this term has important and useful physics consequences. The short-time Fourier transform does not have this feature. The following are some examples that show the cross term feature of the Wigner distribution function.
In order to reduce the cross term problem, many other transforms have been proposed, including the modified Wigner distribution function, the Gabor–Wigner transform, and Cohen’s class distribution.
[edit]Properties of the Wigner distribution function
The Wigner distribution function has several evident properties listed in the following table.
| Remarks | ||
|---|---|---|
| 1 | Projection property |  |
| 2 | Energy property | 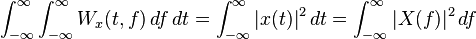 |
| 3 | Recovery property | 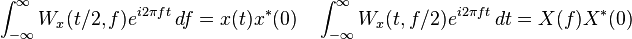 |
| 4 | Mean condition frequency and mean condition time | 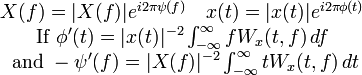 |
| 5 | Moment properties | 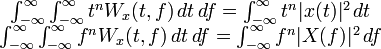 |
| 6 | Real properties | 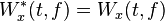 |
| 7 | Region properties | 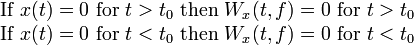 |
| 8 | Multiplication theorem |  |
| 9 | Convolution theorem | 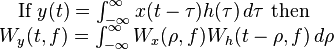 |
| 10 | Correlation theorem | 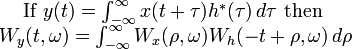 |
| 11 | Time-shifting property |  |
| 12 | Modulation property | 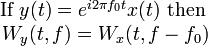 |
[edit]See also
- Time-frequency representation
- Short-time Fourier transform
- Spectrogram
- Gabor transform
- Autocorrelation
- Gabor–Wigner transform
- Cohen's class distribution function
- Wigner quasi-probability distribution
- Transformation between distributions in time-frequency analysis
[edit]References
- B. Boashash, "Note on the Use of the Wigner Distribution for Time Frequency Signal Analysis", IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 36, No. 9, pp. 1518–1521, Sept. 1988. doi:10.1109/29.90380
- B. Boashash, editor, “Time-Frequency Signal Analysis and Processing – A Comprehensive Reference”, Elsevier Science, Oxford, 2003, ISBN 0-08-044335-4.
- S. Qian and D. Chen, Joint Time-Frequency Analysis: Methods and Applications, Chap. 5, Prentice Hall, N.J., 1996.
- E. P. Wigner, “On the quantum correlation for thermodynamic equilibrium,” Phys. Rev., vol. 40, pp. 749–759, 1932.
- T. A. C. M. Classen and W. F. G. Mecklenbrauker, “The Wigner distribution-a tool for time-frequency signal analysis; Part I,” Philips J. Res., vol. 35, pp. 217–250, 1980.
- F. Hlawatsch, G. F. Boudreaux-Bartels: “Linear and quadratic time-frequency signal representation,” IEEE Signal Processing Magazine, pp. 21–67, Apr. 1992.
- R. L. Allen and D. W. Mills, Signal Analysis: Time, Frequency, Scale, and Structure, Wiley- Interscience, NJ, 2004.








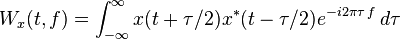



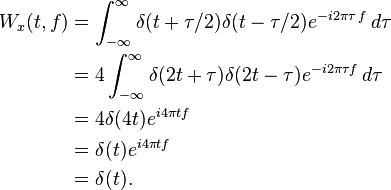


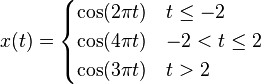
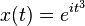














 744
744

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








