分位数回归

分位数（Quantile），亦称分位点，是指将一个随机变量的概率分布范围分为几个等份的数值点，常用的有中位数（即二分位数）、四分位数、百分位数等。

任意一个累计分布函数 $F(x)$ ，满足 $F(\hat{x})=\sigma ,\sigma \in (0,1)$ 的 $\hat{x}$，称为分布 $F$ 的分位数。

$\sigma$ 的含义是该分布中小于$\hat{x}$的数占比为$\sigma$，即$P(x<\hat{x})=\sigma$。

给定一个平稳时间序列，我们通常为考虑回归出它的均值。但在更一般的情况下，我们希望回归出样本对应分布的分位点，因为分位点更能反映出分布的性质。

下面用一个例子来说明：

import numpy as np
import matplotlib.pyplot as plt
%matplotlib inline

gauss = [np.random.randn() for _ in range(100)]
plt.plot(gauss)

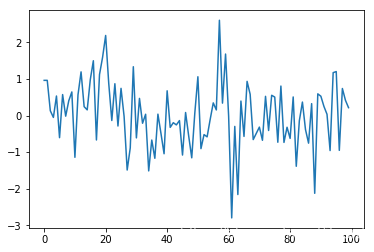
可以直接画出经验概率分布函数

from statsmodels.distributions.empirical_distribution import ECDF

cdf = ECDF(gauss)
plt.plot(cdf.x, cdf.y, label = "statmodels")
plt.xlabel('sample value')

在概率分布函数上找分位点太容易了，在纵轴上确定$\sigma$，回到横轴上找$\hat{x}$

基于梯度下降的分位点回归

在一般的时间序列预测问题中，我们通常是用一个函数取拟合序列，通常学习到的函数是对真实样本均值的估计。

有没有办法让学习函数去逼近真实样本的分位点呢？

只需要使用如下损失函数：
$$L(y,\hat{y})=\sigma \max (y-\hat{y},0)+(1-\sigma )\max (\hat{y}-y,0)$$$$\frac{\partial L(y,\hat{y})}{\partial \hat{y}}=-\sigma \mathbb{I}(y-\hat{y})+(1-\sigma )\mathbb{I}(\hat{y}-y)$$
其中 $\hat{y}$ 是输出，$y$ 为目标值。

rho = 0.75
def grad(rho, z, ze):
    return -rho if ze <= z else 1-rho

ze = 0
lr = 0.1
for z in gauss:
    ze -=  lr*grad(rho, z, ze)

cdf = ECDF(gauss)
plt.plot(cdf.x, cdf.y, label = "statmodels")
plt.plot(ze, rho, 'ro')
plt.plot([-3, ze],[rho, rho],'g--')
plt.plot([ze, ze],[0, rho],'g--')
plt.xlabel('sample value')

rho = 0.1

可以看出，提出下降法很好地找到了序列的分位点，和直接用概率分布函数的结果一致。