链接:https://www.zhihu.com/question/23234701/answer/26017000
另外,e^t是什么样呢?
<img src="https://pic2.zhimg.com/50/67eb5377af1dfca0e2cbea6637076e96_hd.jpg" data-rawwidth="800" data-rawheight="600" class="origin_image zh-lightbox-thumb" width="800" data-original="https://pic2.zhimg.com/67eb5377af1dfca0e2cbea6637076e96_r.jpg"> 但当你在指数上加上i之后呢?
但当你在指数上加上i之后呢?
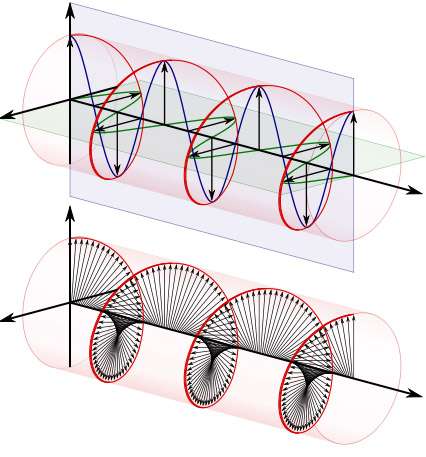
<img src="https://pic4.zhimg.com/50/3af2b68b0bc9802a3cce9d6f56f3bbf1_hd.jpg" data-rawwidth="2000" data-rawheight="999" class="origin_image zh-lightbox-thumb" width="2000" data-original="https://pic4.zhimg.com/3af2b68b0bc9802a3cce9d6f56f3bbf1_r.jpg">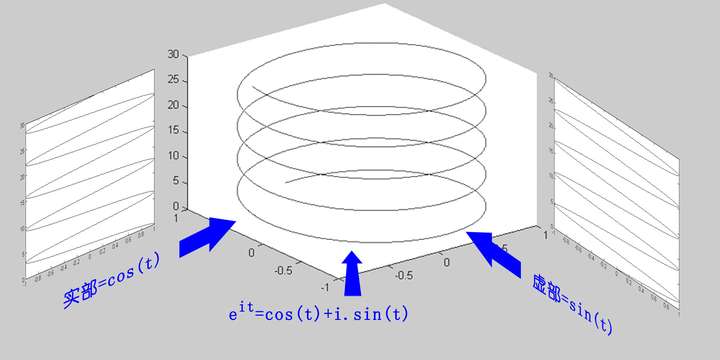 变成了一个螺旋线。是不是和电磁场很像?(想拿欧拉公式去跟女生炫学术的男生注意了:她们,真的,不CARE)
变成了一个螺旋线。是不是和电磁场很像?(想拿欧拉公式去跟女生炫学术的男生注意了:她们,真的,不CARE)
正弦波在频域可以看作是自然数中的“1”,可以构成其他数字的基础元素。当你需要5的时候,你可以看成是1*5(基础元素的五倍)也看以看成2+3(一个基础元素2倍与基础元素3倍的和)。这些用基础元素构成新元素的运算是线性运算。
但是现在你如何用线性运算吧2sin(wt)变换成4sin(wt+pi/6)呢?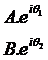
好了,现在如果我想用第一个正弦波利用线性变换为第二个,我们就只需要将A乘对应的系数使其放大至B(本例为乘2),然后将θ1加上一定的角度使其变为θ2(本例为加30度),然后将得到的第二个虚数重新投影回实轴,就完成了在实数中完全无法做到的变换。
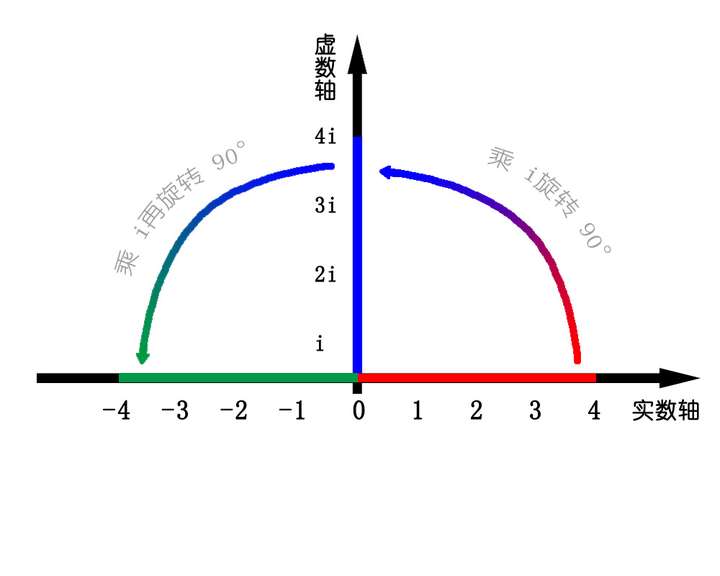
复数最直观的理解就是旋转!
4*i*i = -4
就是“4”在数轴上旋转了180度。
那么4*i就是旋转了90度。

另外,e^t是什么样呢?
<img src="https://pic2.zhimg.com/50/67eb5377af1dfca0e2cbea6637076e96_hd.jpg" data-rawwidth="800" data-rawheight="600" class="origin_image zh-lightbox-thumb" width="800" data-original="https://pic2.zhimg.com/67eb5377af1dfca0e2cbea6637076e96_r.jpg">
 但当你在指数上加上i之后呢?
但当你在指数上加上i之后呢?
<img src="https://pic4.zhimg.com/50/3af2b68b0bc9802a3cce9d6f56f3bbf1_hd.jpg" data-rawwidth="2000" data-rawheight="999" class="origin_image zh-lightbox-thumb" width="2000" data-original="https://pic4.zhimg.com/3af2b68b0bc9802a3cce9d6f56f3bbf1_r.jpg">
 变成了一个螺旋线。是不是和电磁场很像?(想拿欧拉公式去跟女生炫学术的男生注意了:她们,真的,不CARE)
变成了一个螺旋线。是不是和电磁场很像?(想拿欧拉公式去跟女生炫学术的男生注意了:她们,真的,不CARE)
当然,更重要的意义在于复数运算保留了二维信息。
假如我让你计算3+5,虽然你可以轻松的计算出8,但是如果让你分解8你会有无数种分解的方法,3和5原始在各自维度上的信息被覆盖了。
但是计算3+5i的话,你依然可以分解出实部和虚部,就像上图那样。
基于以上两个理由,用复数来描述电场与磁场简直完美到爆棚!
我们即可以让电场强度与复数磁场强度相加而不损失各自的信息,又满足了电场与磁场90度垂直的要求。另外,一旦我们需要让任何一个场旋转90度,只要乘一个“i”就可以了

受
答案的提醒,再补充一点。正弦波在频域可以看作是自然数中的“1”,可以构成其他数字的基础元素。当你需要5的时候,你可以看成是1*5(基础元素的五倍)也看以看成2+3(一个基础元素2倍与基础元素3倍的和)。这些用基础元素构成新元素的运算是线性运算。
但是现在你如何用线性运算吧2sin(wt)变换成4sin(wt+pi/6)呢?
利用欧拉公式,我们可以将任何一个正弦波看作其在实轴上的投影。假如两个不同的正弦波,可以用数学表达为:
好了,现在如果我想用第一个正弦波利用线性变换为第二个,我们就只需要将A乘对应的系数使其放大至B(本例为乘2),然后将θ1加上一定的角度使其变为θ2(本例为加30度),然后将得到的第二个虚数重新投影回实轴,就完成了在实数中完全无法做到的变换。
这种利用复指数来计算正弦波的方法也对电磁波极其适用,因为电磁波都是正弦波,当我们需要一个电磁波在时间上延迟/提前,或是在空间上前移/后移,只需要乘一个复指数就可以完成对相位的调整了。
(图1图3系自制,转载不注明出处注定一辈子学理工没女朋友)
题主关注我的专栏吧,近期会写科普傅里叶的东西…… 与时间无关的故事 - 知乎专栏




















 1341
1341











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








