2510: 弱题
Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 408 Solved: 218
[ Submit][ Status][ Discuss]
Description
有M个球,一开始每个球均有一个初始标号,标号范围为1~N且为整数,标号为i的球有ai个,并保证Σai = M。
每次操作等概率取出一个球(即取出每个球的概率均为1/M),若这个球标号为k(k < N),则将它重新标号为k + 1;若这个球标号为N,则将其重标号为1。(取出球后并不将其丢弃)
现在你需要求出,经过K次这样的操作后,每个标号的球的期望个数。
Input
第1行包含三个正整数N,M,K,表示了标号与球的个数以及操作次数。
第2行包含N个非负整数ai,表示初始标号为i的球有ai个。
Output
应包含N行,第i行为标号为i的球的期望个数,四舍五入保留3位小数。
Sample Input
2 3 2
3 0
Sample Output
1.667
1.333
题名可以。。
先考虑概率dp:dp[x][y]表示第x个回合后,标号为y的小球的期望个个数,那么有
直接转移的话,复杂度是O(nk)的,肯定会超时,不过还好这个递推式显然能转化成矩阵
假设n只有4,那么有递推
矩阵快速幂的话复杂度就降为(n^3logk)了,但n有1000那么大,还是超时。。。
但仔细看这个矩阵可以发现一个特点:它的每一行都是上一行往右移动一位得到的
不但如此,这个矩阵无论自乘多少次,都满足这个性质,所以理论上只需要维护第一行就好了
那么怎么得出新的矩阵第一行?
令k[i]表示矩阵第一行的第i个,那么有
同理
很显然可以看出规律
这样复杂度就是(n²log(k))了
#include<stdio.h>
#include<string.h>
int n;
double ans[1005], Jz[1005], temp[1005];
void Mult(double *a, double *b)
{
int i, j;
memset(temp, 0, sizeof(temp));
for(i=1;i<=n;i++)
{
for(j=1;j<=n;j++)
temp[(i+j-2)%n+1] += a[i]*b[j];
}
memcpy(a, temp, sizeof(temp));
}
int main(void)
{
int m, k, i;
while(scanf("%d%d%d", &n, &m, &k)!=EOF)
{
for(i=1;i<=n;i++)
scanf("%lf", &ans[i]);
Jz[1] = 1-1.0/m;
Jz[2] = 1.0/m;
while(k)
{
if(k%2==1)
Mult(ans, Jz);
Mult(Jz, Jz);
k /= 2;
}
for(i=1;i<=n;i++)
printf("%.3f\n", ans[i]);
}
return 0;
}








 探讨了一道关于球的标号通过特定规则更新后,各标号球期望数量的计算问题。采用概率DP与矩阵快速幂的方法,优化算法至(n²log(k))的时间复杂度。
探讨了一道关于球的标号通过特定规则更新后,各标号球期望数量的计算问题。采用概率DP与矩阵快速幂的方法,优化算法至(n²log(k))的时间复杂度。
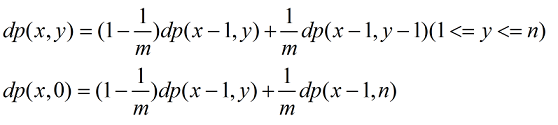
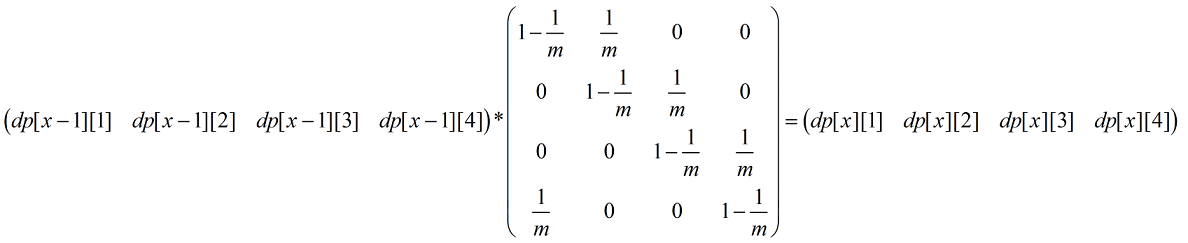

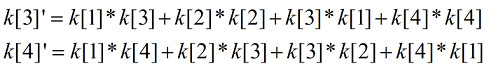
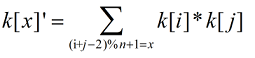
















 1327
1327

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








