时间序列预测建模的完整流程以及数据分析（新手科研必备)

一、本文介绍

本文给大家带来是时间序列建模的完整流程，大家在接触到这个领域的时候，往往都想将数据直接输入到模型中进行训练和预测，对于其中的一些参数都不太理解，这种情况是不可能得到一个好的结果的（本文的内容是我的专栏基础内容，当你拿到我写的任何一个模型无论是深度学习机器学习还是Transformer模型都需要按照本文的流程取分析才能够得到一个好的结果）无论大家是想要发论文还是将时间序列知识应用于其他领域，通过阅读本文都能够有一定的收获。在开始之前先介绍一下我的专栏，本专栏适用于任何群体其中不仅涉及基础知识的完整流程更有接近上百篇的实战案例（总有一篇适合你）本文通过ARIMA模型进行示例。

专栏目录：时间序列预测目录：深度学习、机器学习、融合模型、创新模型实战案例

专栏： 时间序列预测专栏：基础知识+数据分析+机器学习+深度学习+Transformer+创新模型​​​​​​​

下面的图片是一个读者找我调优之后的模型结果对比，大家可以看到经过处理之后同一个模型的不同结果效果真的是天差地别。 

目录

一、本文介绍

​编辑

二、时间序列建模的完整流程

三、 模型选取和数据集

3.1 ARIMA模型

3.2数据集介绍

​四、时间序列建模

4.1 数据获取

4.2 数据预处理

4.2.1 处理数据中的Nan值

4.2.2 检查数据中的异常值和处理

4.3  数据分析

4.3.1 趋势性分析 

4.3.2 季节性分析 

4.3.3 周期性分析 

4.3.4 ACF和PACF

 4.3.5 平稳性检验

 4.4 模型选择

4.5 划分数据集

4.6 模型训练

4.7 模型评估

五、 完整代码

 六、全文总结

---

二、时间序列建模的完整流程

时间序列预测建模的完整过程通常包括以下步骤：

1. 数据收集：

• 首先收集时间序列数据。这些数据应该是按时间顺序排列的连续观察值(有过挺多人问我说我的数据时间不连续可以么，我觉得是不可以如果有这种不连续的情况我建议你提高时间单位从而避免这个情况)。

2. 数据预处理：

•    数据清洗：处理缺失值。
•    异常值数据转换：如对数转换，归一化等，以稳定数据的方差(此处应该是两部分包括异常之检测和异常值处理)。

3. 数据分析：分析数据的特征，如季节性、趋势、周期性等，这一步是重要的你的模型的效果好坏可能百分之60来源于模型，另外的百分之40就来源于这一步。

4. 模型选择：

•    可以选择的模型包括ARIMA（自回归积分滑动平均模型）、季节性ARIMA、指数平滑、Prophet模型、机器学习模型等。
•    还可以使用深度学习方法，如循环神经网络（RNN）、长短期记忆网络（LSTM）。
•    同时还有这两年比较流行的Transformer模型，此方法适合想要发论文的同学。

5. 划分数据集：将数据集划分为测试集验证集训练集

6. 模型训练：使用训练数据集来训练选定的模型。

7. 模型评估：

•     在测试集上评估模型性能。
•     常用的评估指标包括均方误差（MSE）、均方根误差（RMSE）、平均绝对误差（MAE）等。

8. 参数调优：根据模型在测试集上的表现调整参数，以提高预测准确性。

大家需要注意的是时间序列预测是一个动态过程，可能需要多次迭代来优化模型，我在某些实际应用中一个模型甚至要调优上百次才能最终上到实际生产中。

三、 模型选取和数据集

3.1 ARIMA模型

我给大家讲解用的模型是ARIMA模型，这个模型可以算是时间序列领域最重要的模型之一了，先取这个模型的原因是因为它对于参数的设定是十分敏感的，不同的参选择效果可能差异很大后面会有对比给大家看。

3.2数据集介绍

我们本文用到的数据集是某个领域的交通流量数据集 ，该数据集是一个用于时间序列预测交通流量情况的，。

数据内容：该数据集通常包含高峰期和非高峰期的交通流量情况记录。

时间范围和分辨率：数据按半小时为单位进行获取和记录，

以下是该数据集的部分截图->

​四、时间序列建模

4.1 数据获取

这一部分省略了估计大家都都有数据了，我们在这里就讲一下将数据读取进来的代码。

data = pd.read_csv("系统——车流量.csv", index_col=['Date'], parse_dates=['Date'])

在上面的代码中将数据集csv文件读取进来，然后将索引用'Date'列进行替代，替换为的效果为下图，可以看到我们的数据已经变成了一列，原先的Date列变为了索引，这是pandas的基础操作。

4.2 数据预处理

4.2.1 处理数据中的Nan值

moving_avg = data['Volume'].rolling(window=5, min_periods=1).mean()
data['Volume'] = data.fillna(moving_avg)

上面这两句代码是用来处理数据中存在的Nan值，如果数据中存在Nan值是不可以的往往都会导致报错或者结果异常的情况。 

4.2.2 检查数据中的异常值和处理

# 假设 data 是你的 DataFrame，column_name 是需要处理的列名
data['moving_avg'] = data['Volume'].rolling(window=5, min_periods=1).mean()

# 计算 Z-Score
data['z_score'] = (data['Volume'] - data['Volume'].mean()) / data['Volume'].std()

# 将异常值替换为移动平均值
data.loc[data['z_score'].abs() > 1.5, 'Volume'] = data['moving_avg']

这一部分代码是用Z-score检测出异常值同时用移动平均的思想将异常值进行了替换，从而保证我们数据的正常，不受那些因为异常事件导致的特殊值影响。 

4.3  数据分析

这一步就是十分重要的了，分析数据的特征，如季节性、趋势、周期性等（这一步是重要的你的模型的效果好坏可能百分之60来源于模型，另外的百分之40就来源于这一步）。

首先我们来看经过上面的处理之后的数据图像为下图所示->

# 可视化原始数据
data.plot()
plt.title('original data')
plt.show()

 总结：从这张原始的图片上我们可以看出数据又明显的周期性存在单位大概是50个数据左右为一个单位。

4.3.1 趋势性分析 

我们再来看去趋势性分析的图像如下->

# 趋势分析
decomposition = seasonal_decompose(data['Volume'], model='multiplicative', period=50)  # 或者model='multiplicative'取决于数据
trend = decomposition.trend
trend.plot()
plt.title('trend')
plt.show()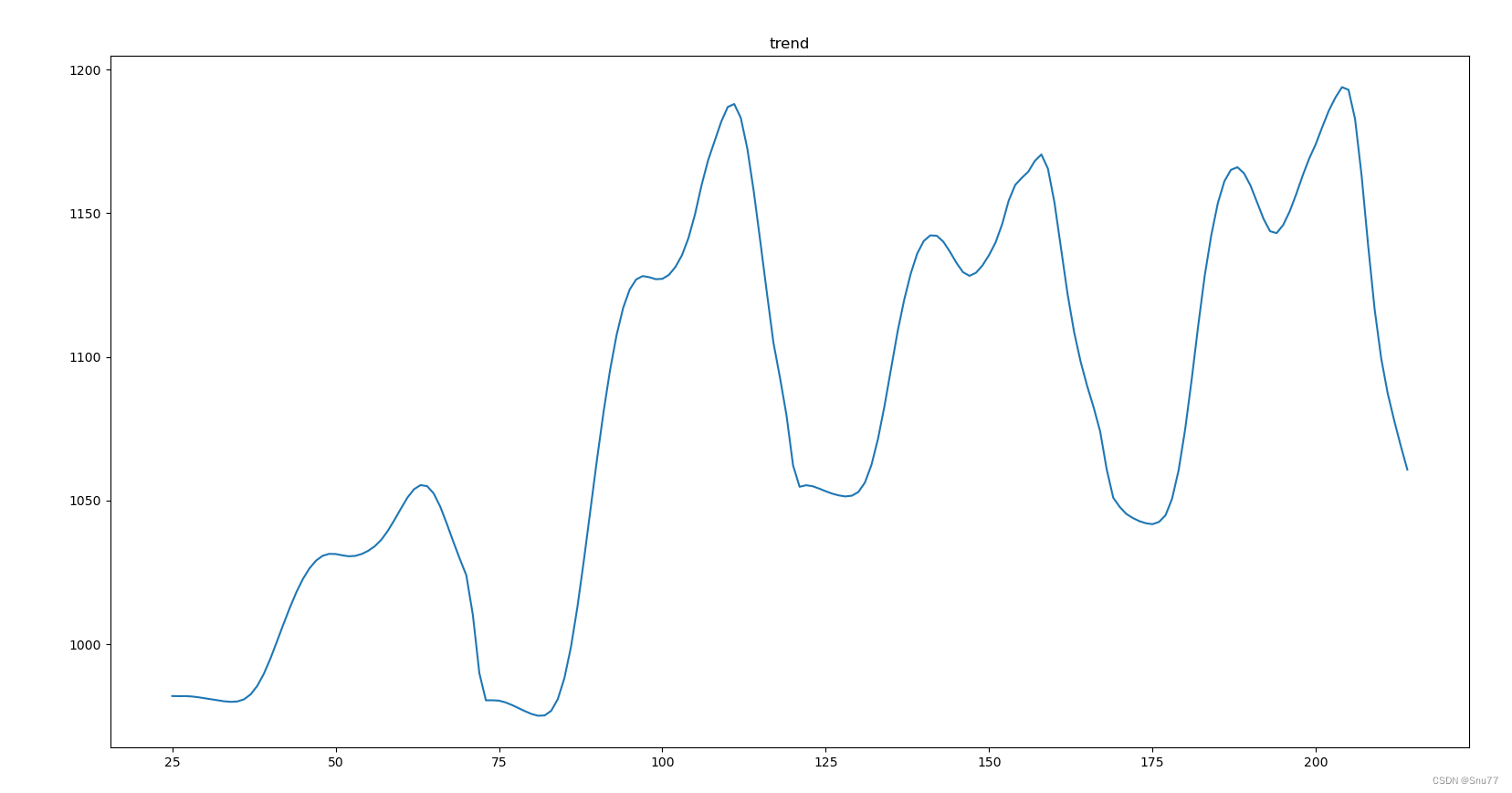

 总结：从这张趋势图上其中显示数据存在波动，但无明显的长期上升或下降趋势。我们看到数据点在某个水平线附近上下波动，这可能表示一个周期性的波动模式，而不是线性或单调的趋势。

4.3.2 季节性分析 

下面的图片是季节性分析图像-> 

# 季节性分析
seasonal = decomposition.seasonal
seasonal.plot()
plt.title('season')
plt.show()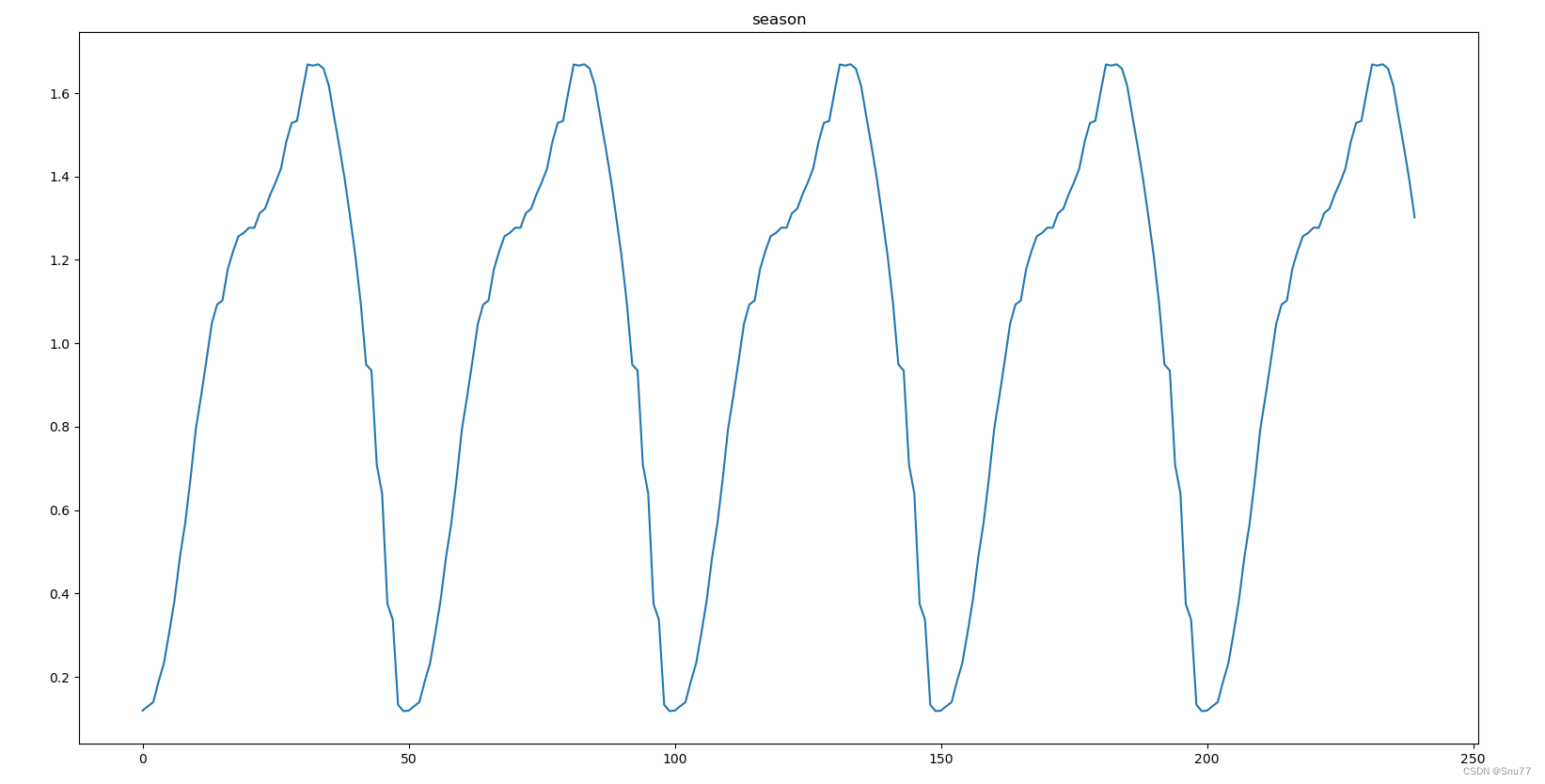

总结：基于季节性分量图像，我们可以使用横坐标的数字来估计一个季节周期。通常，一个季节周期是指从一个峰值到下一个相同峰值的距离，或者从一个谷值到下一个相同谷值的距离。

通过观察季节性分量图像，我们可以估计：

• 从一个峰值到下一个峰值（或谷值到谷值）的距离看起来相对一致。
• 如果我们可以从图像上精确读取两个相邻峰值或谷值的横坐标值，就可以通过它们的差来估算周期长度。

比如，如果第一个峰值在横坐标50处，下一个峰值在横坐标100处，那么季节周期就是100 - 50 = 50个数据点。

4.3.3 周期性分析 

下面的图片是周期性分析图像->

# 周期性分析（残差）
residual = decomposition.resid
residual.plot()
plt.title('Periodicity (residual)')
plt.show()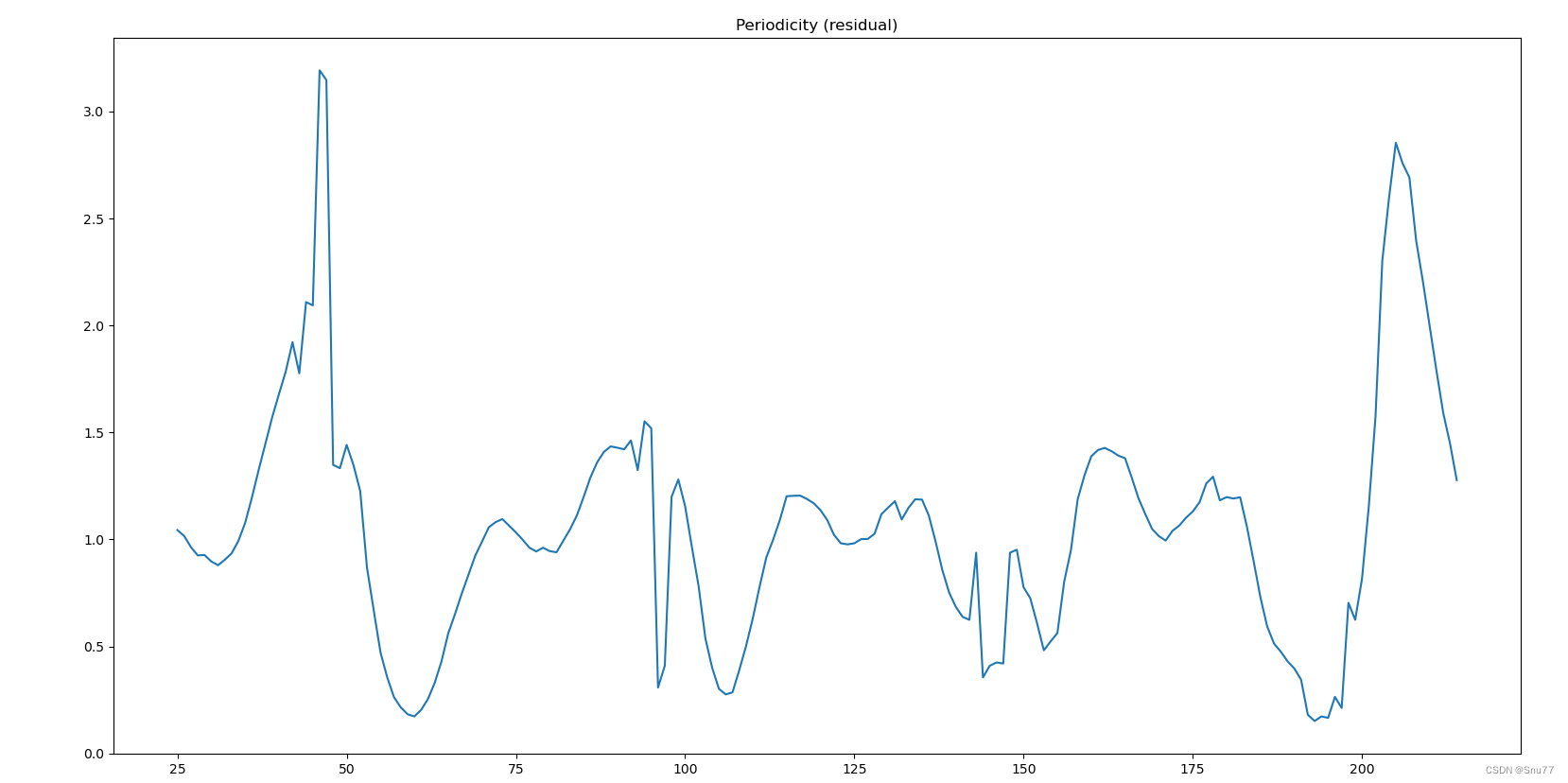

总结：周期性残差的波动表明除了季节性之外，可能还存在其他非固定周期的影响因素，这些可能是因为其他因素引起的所以我们最好可以增加一些其它变量。 

4.3.4 ACF和PACF

下面的图片是ACF和PACF的图像->

# 自相关和偏自相关图
fig, ax = plt.subplots(2, 1, figsize=(12,8))
sm.graphics.tsa.plot_acf(data['Volume'].dropna(), lags=40, ax=ax[0])
sm.graphics.tsa.plot_pacf(data['Volume'].dropna(), lags=40, ax=ax[1])
plt.show()

 总结：从自相关函数（ACF）和偏自相关函数（PACF）图中，我们可以得出以下结论：

 自相关函数 (ACF)：

•   ACF 图显示出显著的逐渐减小的尾部。这通常表明时间序列可能是非平稳的，并可能包含趋势或季节性成分。
•   随着滞后数的增加，自相关系数逐渐下降，但在整个图上仍然显著不为零，这意味着时间序列数据可能具有长期依赖关系。

偏自相关函数 (PACF)：

•   PACF 图在第一个滞后处显示了一个显著的尖峰，之后迅速下降至不显著，这是典型的AR(1)过程的特征，意味着一个数据点主要受到它前一个数据点的影响。
•   在第一滞后之后，大多数滞后的PACF值都不显著（即在蓝色置信区间内），这表明一个阶的自回归模型可能足以捕捉时间序列的相关结构。

综上所述，ACF和PACF的形态表明，时间序列可能适合采用带有差分的自回归模型来建模，如我们本文说的ARIMA模型。通常，这种ACF和PACF的组合会建议我们首先尝试差分时间序列以获得平稳性，然后基于PACF的结果拟合一个AR(1)模型或者根据ACF的衰减模式可能需要考虑更多的AR或MA项。

 4.3.5 平稳性检验

# 平稳性检测
adf_test = adfuller(data['Volume'])
print('ADF 统计量: ', adf_test[0])
print('p-值: ', adf_test[1])

总结： Augmented Dickey-Fuller (ADF) 测试的结果提供了是否拒绝时间序列具有单位根的依据，即时间序列是否是非平稳的。ADF测试的两个关键输出是：

1. ADF 统计量：这是一个负数，它越小，越有可能拒绝单位根的存在。
2. p-值：如果p-值低于给定的显著性水平（通常为0.05或0.01），则拒绝单位根的假设，表明时间序列是平稳的。

在我们的本次测试上的ADF测试结果中：

• ADF 统计量为 -4.8454501013044675，这是一个相对较小的负值。
• p-值为 4.4482852446677935e-05，即大约为 0.0000445。

因为 p-值远小于0.05，我们有强有力的证据拒绝单位根的存在假设，表明时间序列是平稳的。这意味着时间序列数据中很可能不存在随时间变化的趋势或季节性成分，或者已经通过适当的变换（如差分）被去除。

结合前面的ACF和PACF图，我们可以推断这个时间序列数据经过差分或其他转换后可能已经是平稳的，并且可能适合使用ARIMA或类似的自回归模型来进行建模和预测。

 4.4 模型选择

经过前面的分析，结合ACF和PACF图，我们可以推断这个时间序列数据经过差分或其他转换后可能已经是平稳的，并且可能适合使用ARIMA或类似的自回归模型来进行建模和预测，所以我们选择ARIMA模型来进行预测，同时我们选用autoarima进行自动拟合。

4.5 划分数据集

train_ds = data['Volume'][:int(0.9 * len(data))]
test_ds = data['Volume'][-int(0.1 * len(data)):]

我们将9成的数据用来训练模型进行拟合，1成的数据用来测试我们的模型拟合效果。 

4.6 模型训练

我们将从上面分析过来的结果输入的auto_arima里面进行模型的拟合，控制台的拟合效果如图所示。

model = auto_arima(train_ds, trace=True, error_action='ignore', suppress_warnings=True, seasonal=True, m=50,
                   stationary=False, D=2)

model.fit(train_ds)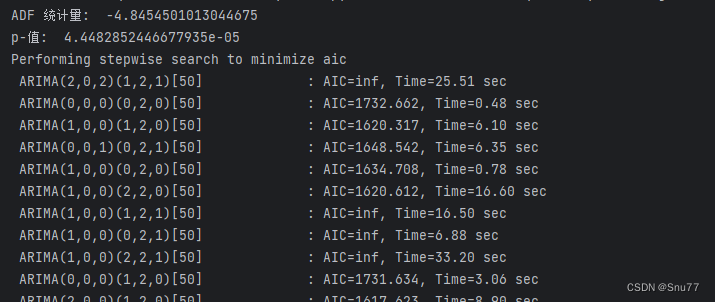

4.7 模型评估

我们训练完模型拟合后我们进行预测和结果可视化，如下图所示->

forcast = model.predict(n_periods=len(test_ds))
# forcast = pd.DataFrame(forcast, index=test_ds.index, columns=['Prediction'])

rms = sqrt(mean_squared_error(test_ds, forcast))
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(15, 7))
# plt.figure('Forecast')
plt.title("forecast value as real")
plt.plot(range(len(train_ds)), train_ds, label='Train')
plt.plot(range(len(train_ds), len(train_ds) + len(test_ds)), test_ds.values, label='Test')
plt.plot(range(len(train_ds), len(train_ds) + len(test_ds)), forcast.values, label='Prediction')
plt.legend()
plt.show()

五、 完整代码

项目的完整代码如下，复制粘贴修改文件之后即可运行。

from math import sqrt
import pandas as pd
import matplotlib.pyplot as plt
import statsmodels.api as sm
from pmdarima import auto_arima
from sklearn.metrics import mean_squared_error
from statsmodels.tsa.seasonal import seasonal_decompose
from statsmodels.tsa.stattools import adfuller

data = pd.read_csv("系统——车流量.csv", index_col=['Date'], parse_dates=['Date'])

moving_avg = data['Volume'].rolling(window=5, min_periods=1).mean()
data['Volume'] = data.fillna(moving_avg)

# 假设 data 是你的 DataFrame，column_name 是需要处理的列名
data['moving_avg'] = data['Volume'].rolling(window=5, min_periods=1).mean()

# 计算 Z-Score
data['z_score'] = (data['Volume'] - data['Volume'].mean()) / data['Volume'].std()
data.reset_index(drop=True,inplace=True)
# 将异常值替换为移动平均值
data.loc[data['z_score'].abs() > 1.5, 'Volume'] = data['moving_avg']

# 可视化原始数据
data.plot()
plt.title('original data')
plt.show()

# 趋势分析
decomposition = seasonal_decompose(data['Volume'], model='multiplicative', period=50)  # 或者model='multiplicative'取决于数据
trend = decomposition.trend
trend.plot()
plt.title('trend')
plt.show()

# 季节性分析
seasonal = decomposition.seasonal
seasonal.plot()
plt.title('season')
plt.show()

# 周期性分析（残差）
residual = decomposition.resid
residual.plot()
plt.title('Periodicity (residual)')
plt.show()

# 自相关和偏自相关图
fig, ax = plt.subplots(2, 1, figsize=(12,8))
sm.graphics.tsa.plot_acf(data['Volume'].dropna(), lags=40, ax=ax[0])
sm.graphics.tsa.plot_pacf(data['Volume'].dropna(), lags=40, ax=ax[1])
plt.show()

# 平稳性检测
adf_test = adfuller(data['Volume'])
print('ADF 统计量: ', adf_test[0])
print('p-值: ', adf_test[1])

train_ds = data['Volume'][:int(0.9 * len(data))]
test_ds = data['Volume'][-int(0.1 * len(data)):]



model = auto_arima(train_ds, trace=True, error_action='ignore', suppress_warnings=True, seasonal=True, m=50,
                   stationary=False, D=2)

model.fit(train_ds)
forcast = model.predict(n_periods=len(test_ds))
# forcast = pd.DataFrame(forcast, index=test_ds.index, columns=['Prediction'])

rms = sqrt(mean_squared_error(test_ds, forcast))
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.rcParams['font.sans-serif'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
plt.figure(figsize=(15, 7))
# plt.figure('Forecast')
plt.title("forecast value as real")
plt.plot(range(len(train_ds)), train_ds, label='Train')
plt.plot(range(len(train_ds), len(train_ds) + len(test_ds)), test_ds.values, label='Test')
plt.plot(range(len(train_ds), len(train_ds) + len(test_ds)), forcast.values, label='Prediction')
plt.legend()
plt.show()

 六、全文总结

到此本文已经全部讲解完成了，希望能够帮助到大家，在这里也给大家推荐一些我其它的博客的时间序列实战案例讲解，其中有数据分析的讲解就是我前面提到的如何设置参数的分析博客，最后希望大家订阅我的专栏，本专栏均分文章均分98，并且免费阅读。

专栏回顾->时间序列预测专栏——包含上百种时间序列模型带你从入门到精通时间序列预测

​