信息熵与压缩编码基础

什么是信息熵？

信息是个很抽象的概念。人们常常说信息很多，或者信息较少来，但却很难说清楚信息到底有多少。比如一本五十万字的中文书到底有多少信息量。
直到1948年，香农提出了“信息熵”的概源念，才解决了对信息的量化度量问题。信息熵这个词是C．E．香农从热力学中借用过来的。热力学中的热熵是表示分子状态混乱程百度的物理量。香农用信息熵的概念来描述信源的不确定度。
信息论之父克劳德·艾尔伍德·香农第一次用数度学语言阐明了概率与信息冗余度的关系。
信息论之父 C. E. Shannon 在 1948 年发表的论文“通信的数学理论（ A Mathematical Theory of Communication ）”中， Shannon 指出问，任何信息都存在冗余，冗余大小与信息中每个符号（数字、字母或单词）的出现概率或者说不确定性有关。
Shannon 借鉴了热力学的概念，把信息中排除了冗余后的平均信息量称为“信息熵”，并给出了计算信息熵的数学表达式答。

两种编码压缩

一串消息包含A，B，C，D，E共5类符号，其内AABBBBAAAACCCCCCCCCEEEEEEDDDDEEEEEEEEEEEEE, 请问其信息熵是多少？如果分别采用香农-范诺编码，霍夫曼编码，压缩率分别是多少？
答案详解：

信息熵：

由于计算机内采用二进制编码 0 和 1，所以对数底数取 2。

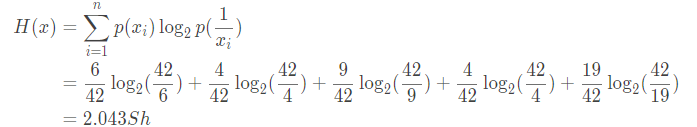
香农-范诺编码：

首先将所有的字母按照出现的次数由多到少、从左到右进行排序，如下图所示：

然后划分两边，使两边出现次数的差尽可能小，如下图所示：

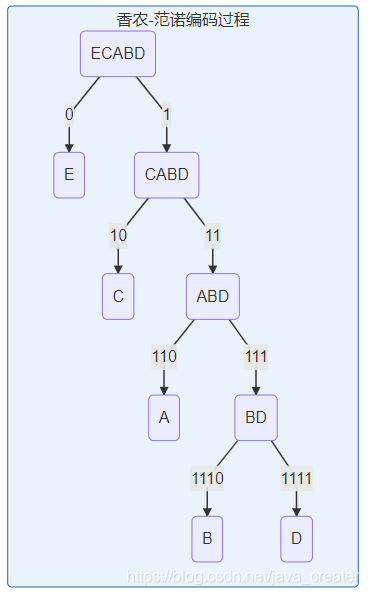
编码完成如下图所示（需要的位数 = 编码位数 × 出现的次数）：

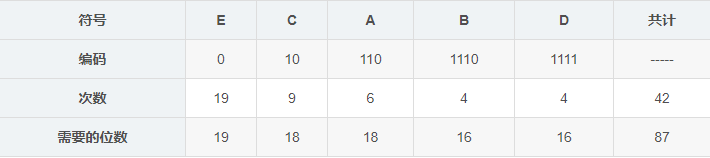
编码前：5 种符号至少需要 3 位二进制编码，共 42 个字符，则需 3 × 42 = 126 3×42=126 3×42=126 位。
编码后：共 87 87 87 位。
压缩比： 126 : 87 = 1.45 : 1 126:87=1.45:1 126:87=1.45:1
霍夫曼编码：

首先所有字母按照从左到右、出现概率从小到打的顺序排列出来，如下图所示：

然后从最小概率的两个符号开始，可选其中一个支路为 0，另一支路为 1，再合并两个支路，并重新排队，多次重复这一过程，直到最后概率为 1，如下图所示

编码完成如下图所示（需要的位数 = 编码位数 × 出现的次数）：

编码前：5 种符号至少需要 3 位二进制编码，共 42 个字符，则需 3 × 42 = 126 3×42=126 3×42=126 位。
编码后：共 87 87 87 位。
压缩比： 126 : 87 = 1.45 : 1 126:87=1.45:1 126:87=1.45:1
结：这道题比较特殊，两种编码方法最后得到的压缩比都一样，但能清晰地了解编码过程即可。

BMP 图像字节计算

问题描述：

一幅 1024×768 的 24 位 RGB 彩色图像一共在内存中占有多少字节？ 如果将其保存为非压缩格式的 BMP 文件，文件有多少字节？

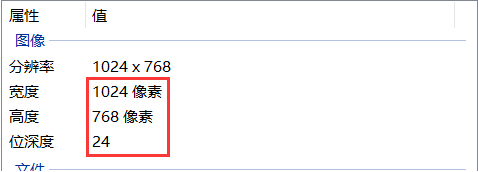
答案详解：