多尺度几何分析（Ridgelet、Curvelet、Contourlet、Bandelet、Wedgelet、Beamlet）

        稀疏基的讨论已经持续了近一个月了，这次讨论多尺度几何分析。但由于下面讨论的这些变换主要面向图像，而本人现在主要关注于一维信号处理，所以就不对这些变换深入讨论了，这里仅从众参考文献中摘抄整理一些相关内容作为自己的一个备忘录，概念也许并不一定理解的准确，若以后杀入图像处理领域再行好好揣摩研究。

一、从小波分析到多尺度几何分析

        小波分析取在从多学科领域中取得巨大成功的一个关键原因在于它比傅里叶分析能更“稀疏”地表示一维分段光滑或者有界变差函数。遗憾的是，小波分析在一维时所具有的优异特性并不能简单的推广到二维或更高维。这是因为一维小波张成的可分离小波(Separable wavelet)只具有有限的方向，不能“最优”表示含线或者面奇异的高维函数，但事实上具有线或面奇异的函数在高维空间中非常普遍，例如，自然物体光滑边界使得自然图像的不连续性往往体现为光滑曲线上的奇异性，而并不仅仅是点奇异。换句话说，在高维情况下，小波分析并不能充分利用数据本身特有的几何特征，并不是最优的或者说“最稀疏”的函数表示方法；而继小波分析之后发展起来的多尺度几何分析（Multiscale Geometric Analysis,MGA）发展的目的和动力正是要致力于发展一种新的高维函数的最优表示方法，为了检测、表示、处理某些高维空间数据，这些空间的主要特点是：其中数据的某些重要特征集中体现于其低维子集中（如曲线、面等）。比如，对于二维图像，主要特征可以由边缘所刻画，而在3-D图像中，其重要特征又体现为丝状物（filaments）和管状物（tubes）。

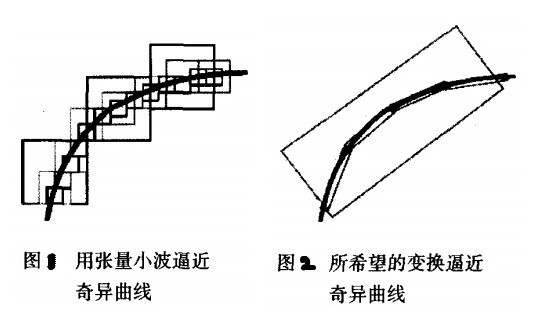
        由一维小波张成的二维小波基具有正方形的支撑区间，不同的分辨率下，其支撑区间为不同尺寸大小的正方形。二维小波逼近奇异曲线的过程最终表现为用“点”来逼近线的过程。在尺度j，小波支撑区间的边长近似为2^-j，幅值超过2^-j的小波系数的个数至少为O(2^j)阶，当尺度变细时，非零小波系数的数目以指数形式增长，出现了大量不可忽略的系数，最终表现为不能“稀疏”表示原函数。因此，我们希望某种变换在逼近奇异曲线时，为了能充分利用原函数的几何正则性，其基的支撑区间应该表现为“长条形”，以达到用最少的系数来逼近奇异曲线。基的“长条形”支撑区间实际上是“方向”性的一种体现，也称为这种基具有“各向异性(anisotropy)”。我们希望的这种变换就是“多尺度几何分析”。

        图像的多尺度几何分析方法分为自适应和非自适应两类，自适应的方法一般先进行边缘检测再利用边缘信息对原函数进行最优表示，实际上是边缘检测和图像表示方法的结合，此类方法以Bandelet和Wdgelet为代表；非自适应的方法并不要先验地知道图像本身的几何特征，而是直接将图像在一组固定的基或框架上进行分解，这就摆脱了对图像自身结构的依赖，其代表为Ridgelet、Curvelet和Contourlet变换。

二、几种多尺度几何分析

1、脊波(Ridgelet)变换

        脊波(Ridgelet)理论由EmmanuelJ Candès于1998年在其博士论文中提出，这是一种非自适应的高维函数表示方法，具有方向选择和识别能力，可以更有效地表示信号中具有方向性的奇异特征。脊波变换首先对图像进行Radon变换，即把图像中的一维奇异性比如图像中的直线映射成Randon域的一个点，然后用一维小波进行奇异性的检测，从而有效地解决了小波变换在处理二维图像时的问题。然而自然图像中的边缘线条以曲线居多，对整幅图像进行Ridgelet分析并不十分有效。为了解决含曲线奇异的多变量函数的稀疏逼近问题，1999年，Candes又提出了单尺度脊波(MonoscaleRidgelet)变换，并给出了其构建方法。另一种方法是对图像进行分块，使每个分块中的线条都近似直线，再对每个分块进行Ridgelet变换，这就是多尺度Ridgelet。脊波变换对于具有直线奇异的多变量函数有良好的逼近性能，也就是说对于纹理（线奇异性）丰富的图像，Ridgelet可以获得比小波更加稀疏的表示；但是对于含曲线奇异的多变量函数，其逼近性能只相当于小波变换，不具有最优的非线性逼近误差衰减阶。

2、曲波(Curvelet)变换

        由于多尺度Ridgelet分析冗余度很大，Candès和Donoho于1999年在Ridgelet变换的基础上提出了连续曲波（Curvelet）变换，即第一代Curvelet变换中的Curvelet99； 2002年，Strack、Candès和Donoho提出了第一代Curvelet变换中的Curvelet02。第一代Curvelet变换实质上由Ridgelet理论衍生而来，是基于Ridgelet变换理论、多尺度Ridgelet变换理论和带通滤波器理论的一种变换。单尺度脊波变换的基本尺度是固定的，而Curvelet变换则不然，其在所有可能的尺度上进行分解，实际上Curvelet变换是由一种特殊的滤波过程和多尺度脊波变换(Multiscale Ridgelet Transform)组合而成：首先对图像进行子带分解；然后对不同尺度的子带图像采用不同大小的分块；最后对每个分块进行Ridgelet分析。如同微积分的定义一样，在足够小的尺度下，曲线可以被看作为直线，曲线奇异性就可以由直线奇异性来表示，因此可以将Curvelet变换称为“Ridgelet变换的积分”。

        第一代Curvelet的数字实现比较复杂，需要子带分解、平滑分块、正规化和Ridgelet分析等一系列步骤，而且Curvelet金字塔的分解也带来了巨大的数据冗余量，因此Candès等人于2002年又提出了实现更简单、更便于理解的快速Curvelet变换算法，即第二代Curvelet (FastCurvelet transform)。第二代Curvelet与第一代Curvelet在构造上己经完全不同。第一代Curvelet的构造思想是通过足够小的分块将曲线近似到每个分块中的直线来看待，然后利用局部的Ridgelet分析其特性，而二代的Curvelet和Ridgelet理论并没有关系，实现过程也无需用到Ridgelet，二者之间的相同点仅在于紧支撑、框架等抽象的数学意义。2005年，Candès和Donoho提出了两种基于第二代Curvelet变换理论的快速离散Curvelet变换实现方法，分别是：非均匀空间抽样的二维FFT算法（Unequally-Spaced FastFourier Transform，USFFT）和Wrap算法（Wrapping-BasedTransform）。对于Curvelet变换，可在网上下载Matlab程序包Curvlab；Curvlab包里有Curvelet的快速离散算法的Matlab程序和C++程序。

3、轮廓波(Contourlet)变换

        2002年，MN Do和Martin Vetterli提出了一种“真正”的图像二维表示方法：Contourlet变换，也称塔型方向滤波器组(Pyramidal Directional Filter Bank, PDFB)。Contourlet变换是利用拉普拉斯塔形分解(LP)和方向滤波器组(DFB)实现的另一种多分辨的、局域的、方向的图像表示方法。

        Contourlet变换继承了Curvelet变换的各向异性尺度关系，因此，在一定意义上，可以认为是Curvelet变换的另一种快速有效的数字实现方式。Contourlet基的支撑区间是具有随尺度变化长宽比的“长条形”结构，具有方向性和各向异性，Contourlet系数中，表示图像边缘的系数能量更加集中，或者说Contourlet变换对于曲线有更“稀疏”的表达。Contourlet变换将多尺度分析和方向分析分拆进行，首先由LP(Laplacian pyramid)变换对图像进行多尺度分解以“捕获”点奇异，接着由方向滤波器组(Directional Filter Bank, DFB)将分布在同方向上的奇异点合成为一个系数。Contourlet变换的最终结果是用类似于轮廓段(Contour segment)的基结构来逼近原图像，这也是所以称之为Contourlet变换的原因。而二维小波是由一维小波张量积构建得到，它的基缺乏方向性，不具有各向异性。只能限于用正方形支撑区间描述轮廓，不同大小的正方形对应小波的多分辨率结构。当分辨率变得足够精细，小波就变成用点来捕获轮廓。

4、条带波(Bandelet)变换

        2000年，ELe Pennec和Stephane Mallat在文献《EL Pennec, S Mallat. Image compression with geometrical wavelets[A].In Proc. OfICIP’ 2000[C]. Vancouver, Canada, September,2000.661-664》中提出了Bandelet变换。Bandelet变换是一种基于边缘的图像表示方法，能自适应地跟踪图像的几何正则方向。Pennec和Mallat认为：在图像处理任务中，若是能够预先知道图像的几何正则性并充分予以利用，无疑会提高图像变换方法的逼近性能。Pennec和Mallat首先定义了一种能表征图像局部正则方向的几何矢量线；再对图像的支撑区间S进行二进剖分S=∪_iΩ_i，当剖分足够细时，每一个剖分区间Ω_i中最多只包含图像的一条轮廓线(边缘)。在所有不包含轮廓线的局部区域Ω_i，图像灰度值的变化是一致正则的，因此，在这些区域内不定义几何矢量线的方向。而对于包含轮廓线的局部区域，几何正则的方向就是轮廓的切线方向。根据局部几何正则方向，在全局最优的约束下，计算区域Ω_i上矢量场τ(x₁,x₂)的矢量线，再沿矢量线将定义在Ω_i的区间小波进行Bandelet化(bandeletization)以生成Bandelet基，以能够充分利用图像本身的局部几何正则性。Bandelet化的过程实际上是沿矢量线进行小波变换的过程，此即所谓的弯曲小波变换(Warped wavelet transform)。于是，所有剖分区域Ω_i上的Bandelet的集合构成了一组L²(S)上的标准正交基。

        Bandelet变换根据图像边缘效应自适应地构造了一种局部弯曲小波变换，将局部区域中的曲线奇异改造成垂直或者水平方向上的直线奇异，再用普通的二维张量小波处理，而二维张量小波基恰恰能有效的处理水平、垂直方向上的奇异。于是，问题的关键归结为对图像本身的分析，即如何提取图像本身的先验信息，怎样剖分图像，局部区域中如何“跟踪”奇异方向等等。然而，在自然图像中，灰度值的突变不总是对应着物体的边缘，一方面，衍射效应使得图像中物体的边缘可能并不明显地表现出灰度的突变；另一方面，许多时候图像的灰度值剧烈变化，并不是由物体的边缘而是由于纹理的变化而产生的。所有基于边缘的自适应方法需要解决的一个共同的问题是如何确定图像中灰度值剧烈变化的区域对应的是物体边缘还是纹理的变化，实际上这是一个非常困难的问题。大部分基于边缘的自适应算法在实际应用中，当图像出现较复杂的几何特征时，如Lena图像，在逼近误差的意义下，性能并不能超过可分离的正交小波分析。在图像的低比特率编码中，用来表示非零系数所在位置的开销远远大于用来表示非零系数值的开销。Bandelet同小波相比有两个优势：（1）充分利用几何正则性，高频子带能量更集中，在相同的量化步骤下，非零系数相对减少；（2）得益于四叉树结构和几何流信息，Bandelet系数可以重新排列，编码时系数扫描方式更灵活。说明Bandelet变换在图像压缩中的潜在优势。

        构造Bandelet变换的中心思想是定义图像中的几何特征为矢量场，而不是看成普通的边缘集合。矢量场表示了图像空间结构的灰度值变化的局部正则方向。Bandelet基并不是预先确定的，而是以优化最终的应用结果来自适应地选择具体的基的组成。Pennec和Mallat给出了Bandelet变换的最优基快速寻找算法，初步实验结果表明，与普通的小波变换相比，Bandelet在去噪和压缩方面体现出了一定的优势和潜力。

5、楔波(Wedgelet)变换

        在多尺度几何分析工具中，Wedgelet变换具有良好的“线”和“面”的特性。

        Wedgelet是DavidL.Donoho教授在研究从含噪数据中恢复原图像的问题时提出的一种方向信息检测模型。Wedgelet变换是一种简明的图像轮廓表示方法。使用多尺度Wedgelet对图像进行分段线性表示，能够根据图像内容自动确定分块大小，较好地捕捉图像中的线和面的特征。克服了滑动窗口方法存在的不足。

        多尺度Wedgelet变换由两部分组成：多尺度Wedgelet分解和多尺度Wedgelet表示。多尺度Wedgelet分解将图像划分成不同尺度的图像块，并将每个图像块投影成各个允许方位的Wedgelet；多尺度Wedgelet表示则根据分解结果，选择图像的最佳划分，并为每个图像块选择出最优的Wedgelet表示，从而完成图像的区域分割。

        什么是Wedgelet？说白了，就是在一个图像子块(dyadic square)画条线段，把它分成两个楔块，每一个楔块用唯一的灰度值表示。线的位置，两个灰度值，就近似刻画了这个子块的性质。

6、小线（Beamlet）变换

        小线变换（BeamletsTransform）是斯坦福大学的David L.Donoho教授1999年首次提出的，已经得到了初步的应用。由小线变换引入的小线分析（Beamlets Analysis）也是一种多尺度分析，但又不同于小波分析的多尺度概念，可以理解为小波分析多尺度概念的延伸，小线分析以各种方向、尺度和位置的小线段为基本单元来建立小线库，图像与库中的小线段积分产生小线变换系数，以小线金字塔方式组织变换系数，再通过图的形式从金字塔中提取小线变换系数，从而实现多尺度分析。这是一种能较好进行二维或更高维奇异性分析的工具。

        根据小线理论及其研究结果来看，它对于处理强噪背景的图像有无可比拟的优势。但是小线变换的前期准备工作，如小线字典、小线金字塔扫描这些部分的工作量太过于庞大，不利于研究。如果能将这部分简化，或者做成固定的模块引用的话，相信小线分析能够很快的扩展其应用领域。总的来说小线分析的研究还处于初步阶段，相关的研究成果也不多，应用研究领域有待于进一步拓展。

        在Beamlet分析中，线段类似于点在小波分析中的地位。Beamlet 能够提供基于二进组织的线段的局部尺度、位置和方向表示，线的精确定位易实现，且算法实现不复杂，所以基于Beamlet 的线特征提取值得研究。

        Beamlet基是一个具有二进特征的多尺度的有方向的线段集合，二进特征体现在线段的始终点坐标是二进的，尺度也是二进的。

        Donoho 提出了连续Beamlet变换及其在多尺度分析中的应用，为减少计算量及更适于计算机处理，Xiaoming Huo 提出了离散Beamlet变换。

        从Beamlet基的框架得知，每条Beamlet把每个二进方块分为两个部分，每个部分都称为Wedgelet，这两部分为互补的Wedgelet，从而每个Beamlet对应两个互补的Wedgelet，使Beamlet基与Wedgelet对应起来Wedgelet变换具有多尺度的特性；还可以看出Wedgelet基是片状基，与Beamlet的线状基不同。

参考文献：

【1】焦李成，谭山.图像的多尺度几何分析：回顾和展望[J]. 电子学报，2003，31(12A)：1975-1981.

【2】焦李成，谭山，刘芳. 脊波理论：从脊波变换到Curvelet变换[J].工程数学学报，2005，22(5)：761-773.

【3】隆刚，消磊，陈学佺. Curvelet变换在图像处理中的应用综述[J]. 计算机研究与发展，2005，42(8)：1331-1337.

【4】刘云霞.基于有限脊波变换和压缩感知理论的智能交通监控系统技术研究[D].山东大学，2012.

【5】hongbo01.第三章 脊波和曲波变换，百度文库.

【6】hongbo01.第7章Bandelet变换及其应用，百度文库.

【7】hongbo01.第8章Beamlet及其应用，百度文库.

【8】hongbo01.第九章Contourlet变换及其应用，百度文库.

【9】胡镠. Curvelet学习笔记，网易博客.

【10】屈庆春，彭玉华. 基于Wedgelet变换的图像边缘检测[J].生物医学工程研究，2005，24(1)：8-10.

【11】杨明，尹勇，彭玉华，周新虹. Beamlet变换与多尺度线特征提取[J].电子学报，2007，35(1)：100-103.

【12】侯彪，刘佩，焦李成. 基于改进Wedgelet变换的SAR图像边缘检测[J].红外与毫米波学报，2009，28(5)：396-400.

【13】韩敏，林晓峰. 一种基于Wedgelet变换的遥感图像分类算法[J].红外与毫米波学报，2008，27(4)：280-284.

【14】wy19811007.新小波Wedgelet，百度文库.

【15】hongbo01.第2章多分辨分析和塔式算法，百度文库.

【16】hongbo01.第4章3D-DFB和Surfacelet变换，百度文库.