时间序列分析实战（六）：ARIMA乘法（疏系数）模型建模及预测

🍉CSDN小墨&晓末:https://blog.csdn.net/jd1813346972

   个人介绍: 研一｜统计学｜干货分享
         擅长Python、Matlab、R等主流编程软件
         累计十余项国家级比赛奖项，参与研究经费10w、40w级横向

1 目的

  该篇文章主要展示针对时序进行ARIMA乘法模型建模，并根据实际情况进行改进。案例数据同 时间序列分析实战（三）：时序因素分解法：某欧洲小镇1963年1月至1976年12月每月旅馆入住的房间数构成时间序列$x_t$，我们在 时间序列分析实战（五）：ARIMA加法（疏系数）模型建模利用此数据构建了ARIMA加法模型。现考虑演示根据该数据建立ARIMA乘法模型。

2 原序列差分处理

  从 时间序列分析实战（三）：时序因素分解法一文中可知，该序列具有趋势和季节效应，进行1阶差分提取趋势效应，12步差分提取季节效应。

  运行程序：

#对原数据进行1阶12步差分
y=diff(diff(data1,12))
plot(y,sub='图1 入住房间数差分后序列时序图')

  运行结果：

图1 入住房间数差分后序列时序图

3 差分后序列平稳性检验

  运行程序：

#差分后序列平稳性检验
library(aTSA)
adf.test(y)

  运行结果：

## Augmented Dickey-Fuller Test 
## alternative: stationary 
##  
## Type 1: no drift no trend 
##      lag    ADF p.value
## [1,]   0 -19.56    0.01
## [2,]   1 -11.01    0.01
## [3,]   2 -10.63    0.01
## [4,]   3  -9.08    0.01
## [5,]   4 -10.57    0.01
## Type 2: with drift no trend 
##      lag    ADF p.value
## [1,]   0 -19.50    0.01
## [2,]   1 -10.98    0.01
## [3,]   2 -10.60    0.01
## [4,]   3  -9.05    0.01
## [5,]   4 -10.53    0.01
## Type 3: with drift and trend 
##      lag    ADF p.value
## [1,]   0 -19.44    0.01
## [2,]   1 -10.94    0.01
## [3,]   2 -10.56    0.01
## [4,]   3  -9.01    0.01
## [5,]   4 -10.49    0.01
## ---- 
## Note: in fact, p.value = 0.01 means p.value <= 0.01

4 差分后序列白噪声检验

  运行程序：

#差分后序列纯随机性检验
for(k in 1:2) print(Box.test(y,lag=6*k,type="Ljung-Box"))

  运行结果：

## 
##  Box-Ljung test
## 
## data:  y
## X-squared = 56.87, df = 6, p-value = 1.941e-10
## 
## 
##  Box-Ljung test
## 
## data:  y
## X-squared = 76.751, df = 12, p-value = 1.713e-11

  通过1阶12步差分后序列时序图(图1)显示差分后的序列没有明显趋势和周期特征了，ADF检验结果显示差分后序列平稳，纯随机性检验结果显示差分后序列为非白噪声序列，适合建模。

5 ARIMA乘法模型建立

  运行程序：

par(mfrow=c(2,1))
acf(y,lag=36)
title(sub="图2 入住房间数差分后序列自相关图(ACF)")
pacf(y,lag=36)
title(sub="图3 入住房间数差分后序列偏自相关图(PACF)")

  运行结果：

图2 入住房间数差分后序列自相关图(ACF)）

图3 入住房间数差分后序列偏自相关图(PACF)

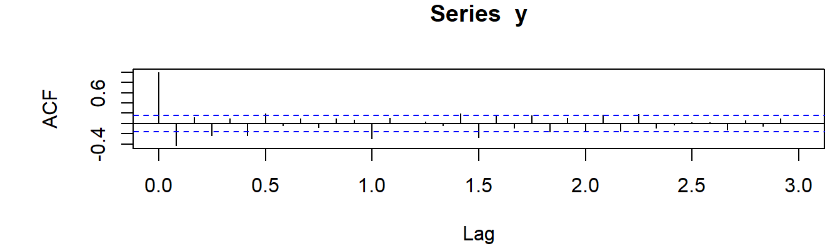
  为考虑季节相关特征，这时考察延迟12阶、24阶等以周期长度为单位的自相关系数和偏自相关系数的特征。图2和图3显示,自相关图表现拖尾性质，偏自相关图表现截尾性质，若把偏自相关系数看作1周期截尾，结合前面的差分信息，经过多次尝试后，尝试拟合ARIMA乘法模型:：$ARIMA(3,1,2)\times (1,1,0{)}_{12}$

6 ARIMA乘法模型拟合

  运行程序：

fit4=arima(data1,order = c(3,1,2),seasonal = list(order=c(1,1,0),period=12))
fit4

  运行结果：

## 
## Call:
## arima(x = data1, order = c(3, 1, 2), seasonal = list(order = c(1, 1, 0), period = 12))
## 
## Coefficients:
##          ar1     ar2      ar3      ma1     ma2     sar1
##       0.8229  0.0030  -0.3107  -1.7905  0.7905  -0.4073
## s.e.  0.1155  0.1036   0.0851   0.1110  0.1102   0.0816
## 
## sigma^2 estimated as 213.2:  log likelihood = -640.63,  aic = 1295.25

7 ARIMA乘法模型显著性检验

  运行程序：

#模型显著性检验
ts.diag(fit4)
title(sub="图4 ARIMA(3,1,2)×(1,1,0)_12模型显著性检验")

  运行结果：

图4 ARIMA(3,1,2)×(1,1,0)_12模型显著性检验

  此时模型${\varphi }_2$估计值在两倍标准差内，考虑建立ARIMA乘法疏系数模型：$ARIMA((1,3),1,2)\times (1,1,0{)}_{12}$

8 ARIMA乘法疏系数模型

  运行程序：

#拟合乘法ARIMA模型
fit5=arima(data1,order = c(3,1,2),seasonal = list(order=c(1,1,0),period=12),
           transform.pars = F,fixed=c(NA,0,NA,NA,NA,NA))
fit5

  运行结果：

## 
## Call:
## arima(x = data1, order = c(3, 1, 2), seasonal = list(order = c(1, 1, 0), period = 12), 
##     transform.pars = F, fixed = c(NA, 0, NA, NA, NA, NA))
## 
## Coefficients:
##          ar1  ar2      ar3      ma1    ma2     sar1
##       0.8263    0  -0.3090  -1.7930  0.793  -0.4072
## s.e.  0.0941    0   0.0611   0.1078  0.107   0.0807
## 
## sigma^2 estimated as 213.2:  log likelihood = -640.63,  aic = 1293.25

9 ARIMA乘法疏系数模型显著性检验

  运行程序：

#模型显著性检验
ts.diag(fit5)
title(sub="图5 ARIMA((1,3),1,2)模型显著性检验")

  运行结果：

图5 ARIMA(3,1,2)×(1,1,0)_12模型显著性检验

  此时，模型参数估计值在2倍标准差外，且残差为白噪声序列，aic=1293.25。最终$ARIMA((1,3),1,2)\times (1,1,0{)}_{12}$模型为：

$$\nabla {\nabla }_{12}{x}_t=\frac{1-0.79B-0.79B^2}{1-0.83B+0.31B^3}(1-0.41B^{1}2){ϵ}_t,Var({ϵ}_t)=213.2$$

综上所述，从AIC的角度来看，疏系数的ARIMA乘法模型的AIC值更小，为1293.25，因此在该序列的拟合模型中，选用ARIMA乘法模型$ARIMA((1,3),1,2)\times (1,1,0{)}_{12}$模型来进行预测。

10 ARIMA乘法疏稀疏模型预测

  运行程序：

library(forecast)
fore2=forecast::forecast(fit5,h=36)
fore2$mean

  运行结果：

##            Jan       Feb       Mar       Apr       May       Jun       Jul
## 1977  827.6433  768.2262  771.2960  860.6892  838.8292  963.9901 1128.1026
## 1978  853.5056  785.6367  792.7410  886.3393  869.2913  985.3445 1154.0686
## 1979  875.9526  811.5455  817.0429  908.9636  889.9786 1009.7484 1176.5900
##            Aug       Sep       Oct       Nov       Dec
## 1977 1159.3063  892.6915  897.5451  778.5312  884.5493
## 1978 1178.2927  915.9224  915.4218  804.8587  914.4704
## 1979 1203.6458  939.5356  941.2077  827.1998  935.3489

  运行程序：

plot(fore2,lty=2,sub='图5 入住房间数序列疏系数的ARIMA乘法模型预测效果图')
lines(fore2$fitted,col=4)

  运行结果：

图6 入住房间数序列疏系数的ARIMA乘法模型预测效果图

  根据结果显示，疏稀疏的ARIMA乘法模型有较好拟合效果。