人:“A group of men playing Frisbee in the park.”
计算机:“A group of young people playing a game of Frisbee.”

卷积神经网络也应用于为物体贴标签,下面是实例,我想它如果运用于Google眼镜的话,“当我们看到一幅自然图片,眼镜就会显示你看到的所有东西,并给于标签,那么人的学习认知能力有多强大啊。
图片贴标签实例
目前,卷积神经网络无疑成为计算机视觉以及模式识别领域的热门话题,它对处理多分类,大型的图片分类有着非常好的效果,本文主要包括以下几个内容:
1.卷积神经网络的整体框架
1.1 卷积层
1.2 采样层
1.3 全连接层
2.卷积神经网络的建立(前馈网络)
3.卷积和相关的区别
4.核函数的选定
5.BP反馈调节参数(反馈网络)
6.优化方法的选定
7.实验
1.卷积神经网络的整体框架
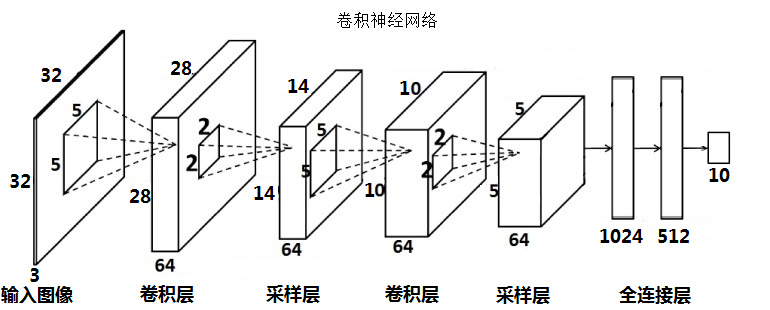
下面先给出图,然后再说明这个框架。
在上图的这个框架下,输入的是RGB图像,用到颜色信息,如果你处理的灰度图像,那么你的输入层数就为1层,但是这会降低最后识别率。输入图像(input)为32×32×3,当然你要处理的图像尺寸不一样,那么你的输入层的大小就不一样了,输入的图像经过一个3×5×5的滤波器就得到了一个featuremap,由于此处的滤波未填充边缘,一个滤波器就产生一张28×28的featuremap,那么用64个滤波器进行卷积,就会产生64张featuremaps,这就叫做特征图(卷积层C)。不同的滤波器提取出来的特征当然不一样,这时就需要通过采样层了,采样层采用的是2×2的核,采用的均值采样,最终得到的featuremaps变为14×14×64(采样层S),得到特征再利用64个5×5×64的滤波器滤波得到64张10×10×64(卷积层C),这个时候是立体的滤波,不同于平面滤波,但是原理都一样。又通过2×2的核采样得到64张5×5的featuremaps(采样层S),这时就有64×5×5=1600个神经元了,(当然你还可以用5×5×64的滤波器滤波,这时得到featuremap就为1×1了,当然这只是讨论),这1600个神经元,是最后一层采样层的每一张featuremap拉伸成一个向量的结果,一张featuremap的向量为25维,那么64张就为1600维。接下来做的工作就是降维了,可以通过普通神经网络进行降维,此处称为“全连接层”,这里我设定第一层全连接层f1的神经元个数为1024,第二层全连接层f的神经元个数为512,第二层神经元就称为一张图片的特征值,这时你要连接一个分类器,此处的分类器为softmax分类器,可以实现多分类的。
这个框架可以参见前两篇博文:
http://blog.csdn.net/hlx371240/article/details/41208515
http://blog.csdn.net/hlx371240/article/details/40015395
这样一个卷积神经网络的框架就介绍完了,里面的参数(如卷积核的大小,卷积核的数量,采样层的采样方式,如均值,max值,全连接层神经元的个数,层数)大家都可以自己进行设计,没有统一的标准。
下面是MATLAB给出的网络结构
- <span style="font-family:Times New Roman;font-size:14px;"><span style="font-family:Times New Roman;"><span style="font-size:18px;">cnn.layers = {
- struct('type', 'i','inputmaps',3 ,'inputsize',32) %input layer
- struct('type', 'c', 'outputmaps', 64, 'kernelsize', 5) %convolution layer
- struct('type', 's', 'scale', 2) %sub sampling layer
- struct('type', 'c', 'outputmaps', 64, 'kernelsize', 5) %convolution layer
- struct('type', 's', 'scale', 2) %subsampling layer
- struct('type', 'f1', 'neuron', 1024) %full-connection layer
- struct('type', 'f', 'neuron', 512) %full-connection layer
- struct('type', 'o', 'scale', 10)
- }; </span></span></span>
1.1卷积层
此处的卷积跟图像里面的卷积一样,但是不是事先训练好的,而是随机产生的卷积核,而且卷积核的大小都是自己设定的。你可以设定为任意尺寸大小,如5×5,6×6等,当然卷积核不一定都为正方形,可以是矩形,如7×6,8×9等等都行,这只是单层核, 也可以是多层核,假如输入图像是RGB的图像,含有3通道,那么你需要设定一个3D核,一个3D核与输入图像就得到一张特征图featuremap,64个3D核就得到64张featuremaps。
另外我们来看卷积过后的图像大小,其实在前面的博文中已经指出来了,卷积神经网络做卷积的时候,原图是不进行扩充的,所以卷积过后图片是会减小的,比如,20×20的图片,现在有5×5的核去卷积,那么就得到(20-5)+1×(20-5)+1=16×16大小的featuremap,对于3D核也是一样的。
可以参见博文:http://blog.csdn.net/hlx371240/article/details/41208515
1.2 采样层
采样层一般是正方形的核函数,这个核函数可以是均值核,也可以是求取核区域的最大值,用均值核叫做meanpooling,用求取区域最大值的核称为maxpooling。对于卷积得到的大小为30×30的图像,假如我们采用2×2的核函数采样,那么就得到15×15大小的图像,如果采用3×3的核函数,就产生了10×10大小的图像,如果有人用4×4的核,那么30不能整除4,所以选择这个尺寸的核函数不太合适,你可以选择5×5的核。采样是图像特征的进一步抽取。
可以参见博文:http://blog.csdn.net/hlx371240/article/details/41208515
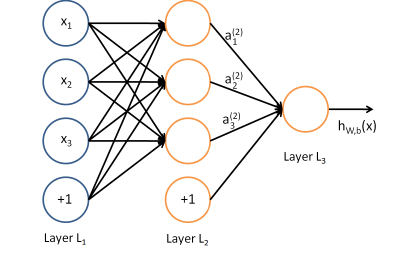
2.卷积神经网络的建立(前馈网络)
卷积神经网络分为前馈网络和反馈网络,前馈网络可以说是得到最终概率值然后进行判别。
第一层:一个5×5×3的卷积核和输入的32×32×3的RGB图像做卷积,卷积核是3层,RGB也为3层,他们分别做卷积然后相加,这样就得到一张28×28的图像,此处的图像就为一个通道了。我们可以用64个卷积核对图像进行卷积,这样就得到64张28×28大小的图像。(每一个卷积后得到值都要经过非线性变换,如一些非线性的核函数)卷积后再用2×2的采样核,得到14×14大小的图像,由于上一层有64张featuremaps,采样不会改变featuremaps的数量,还是64个featuremaps。然后经过第二次卷积,这时的卷积核是5×5×64的大小,是个3D的核函数,一共含有64层,每一层与上层采样的64张featuremaps分别做卷积得到一张featuremap,同样的用64个5×5×64核函数就得到64张featuremaps,(每一个卷积后得到值都要经过非线性变化)。卷积后产生了64张10×10大小的图像,这时再经过采样得到64个5×5大小的子图,一共加起来为1600个神经元,当然此时还有可以用64个5×5×64的卷积核卷积,得到64个单独的神经元。现在我没有加入这层,而是1600个神经元。这时就可以用普通的神经网络再进行降维。
当然最后一层接的是Softmax分类器。
可以参见博文:http://blog.csdn.net/hlx371240/article/details/40015395
Ng的文章Sparse autoencoder:http://nlp.stanford.edu/~socherr/sparseAutoencoder_2011new.pdf
cnnff.m
- <span style="font-family:Times New Roman;font-size:14px;">function net = cnnff(net, x)
- [A B C D]=size(x);
- inputmaps = net.layers{1}.inputmaps; % 输入层只有一个特征map,也就是原始的输入图像
- n = numel(net.layers); % 层数
- for i=1:inputmaps
- channel=reshape(x(:,:,i,:),net.layers{1}.inputsize,net.layers{1}.inputsize,D);
- net.layers{1}.a{i}=channel; % 网络的第一层就是输入,但这里的输入包含了多个训练图像
- end
- for l = 2 : n % for each layer
- if strcmp(net.layers{l}.type, 'c') % 卷积层
- % !!below can probably be handled by insane matrix operations
- % 对每一个输入map,或者说我们需要用outputmaps个不同的卷积核去卷积图像
- for j = 1 : net.layers{l}.outputmaps % for each output map
- % create temp output map
- % 对上一层的每一张特征map,卷积后的特征map的大小就是
- % (输入map宽 - 卷积核的宽 + 1)* (输入map高 - 卷积核高 + 1)
- % 对于这里的层,因为每层都包含多张特征map,对应的索引保存在每层map的第三维
- % 所以,这里的z保存的就是该层中所有的特征map了
- z = zeros(size(net.layers{l - 1}.a{1}) - [net.layers{l}.kernelsize - 1 net.layers{l}.kernelsize - 1 0]);
- for i = 1 : inputmaps % for each input map
- % convolve with corresponding kernel and add to temp output map
- % 将上一层的每一个特征map(也就是这层的输入map)与该层的卷积核进行卷积
- % 然后将对上一层特征map的所有结果加起来。也就是说,当前层的一张特征map,是
- % 用一种卷积核去卷积上一层中所有的特征map,然后所有特征map对应位置的卷积值的和
- % 另外,有些论文或者实际应用中,并不是与全部的特征map链接的,有可能只与其中的某几个连接
- z = z + convn(net.layers{l - 1}.a{i}, net.layers{l}.k{i}{j}, 'valid');
- end
- % add bias, pass through nonlinearity
- % 加上对应位置的基b,然后再用sigmoid函数算出特征map中每个位置的激活值,作为该层输出特征map
- net.layers{l}.a{j} = relu(z + net.layers{l}.b{j});
- end
- % set number of input maps to this layers number of outputmaps
- inputmaps = net.layers{l}.outputmaps;
- elseif strcmp(net.layers{l}.type, 's') % 下采样层
- % downsample
- for j = 1 : inputmaps
- % !! replace with variable
- % 例如我们要在scale=2的域上面执行mean pooling,那么可以卷积大小为2*2,每个元素都是1/4的卷积核
- z = convn(net.layers{l - 1}.a{j}, ones(net.layers{l}.scale) / (net.layers{l}.scale ^ 2), 'valid');
- % 因为convn函数的默认卷积步长为1,而pooling操作的域是没有重叠的,所以对于上面的卷积结果
- % 最终pooling的结果需要从上面得到的卷积结果中以scale=2为步长,跳着把mean pooling的值读出来
- net.layers{l}.a{j} = z(1 : net.layers{l}.scale : end, 1 : net.layers{l}.scale : end, :);
- end
- elseif strcmp(net.layers{l}.type, 'f1')
- net.layers{l-1}.fv = [];
- for j = 1 : numel(net.layers{l-1}.a) % 最后一层的特征map的个数
- sa = size(net.layers{l-1}.a{j}); % 第j个特征map的大小
- % 将所有的特征map拉成一条列向量。还有一维就是对应的样本索引。每个样本一列,每列为对应的特征向量
- net.layers{l-1}.fv = [net.layers{l-1}.fv; reshape(net.layers{l-1}.a{j}, sa(1) * sa(2), sa(3))];
- end
- net.layers{l}.a = relu(net.layers{l-1}.ffW * net.layers{l-1}.fv + repmat(net.layers{l-1}.ffb, 1, size(net.layers{l-1}.fv, 2)));
- elseif strcmp(net.layers{l}.type, 'f')
- net.layers{l}.a = relu(net.layers{l-1}.ffW * net.layers{l-1}.a+repmat(net.layers{l-1}.ffb, 1, size(net.layers{l-1}.a, 2)));
- elseif strcmp(net.layers{l}.type, 'o')
- net.layers{l}.a = relu(net.layers{l-1}.ffW * net.layers{l-1}.a+repmat(net.layers{l-1}.ffb, 1, size(net.layers{l-1}.a, 2)));
- end
- end
- end</span>
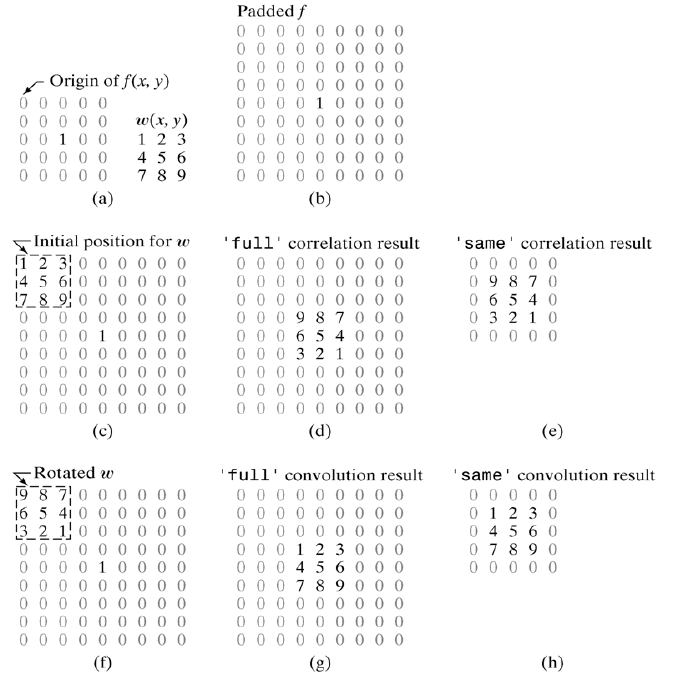
下面直接给一张图来说明卷积和相关的区别
相关是核直接与原图像做线性运算,而卷积是需要把核做180度然后再做线性相加运算。
rot180.m
- <span style="font-family:Times New Roman;">function X = rot180(X)
- X = flipdim(flipdim(X, 1), 2);
- end</span>
4.核函数的选定
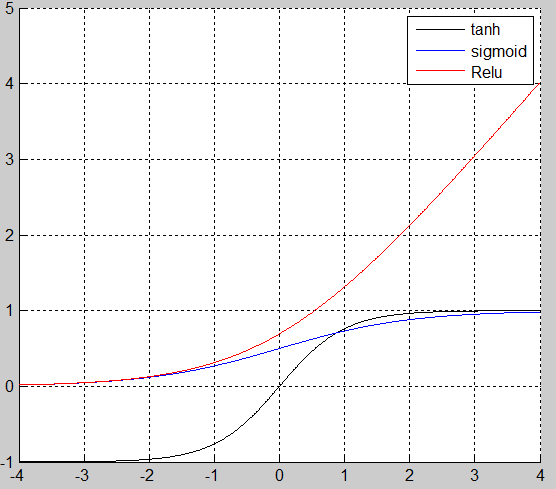
下面介绍3种核函数tanh,sigmiod,Relu核函数,分别给出它们的图像
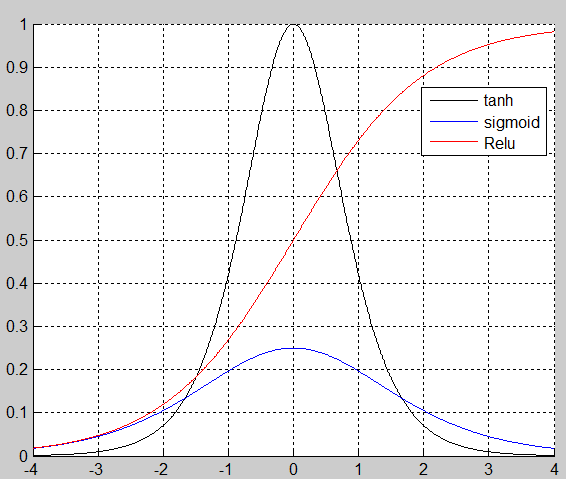
下面分别画出它们的导数的图像
一般的神经网络选用的是sigmoid核函数,但是对于深度网络来说,反馈时的系数太小,导致从最后一层反馈到第一层的参数已经太小,深度网络很多人选用Relu核,在这篇文章中Imagenet classification with deep convolutional neural networks选用的Relu核,并产生了很好的效果,代码在https://code.google.com/p/cuda-convnet/中,这个代码是用C++和python写的。
5.BP反馈调节参数(反馈网络)
参考文章:http://nlp.stanford.edu/~socherr/sparseAutoencoder_2011new.pdf
Jake Bouvrie, Notes on Convolutional Neural Networks
现在我只讲卷积反馈,普通神经网络的反馈可以参见文章http://nlp.stanford.edu/~socherr/sparseAutoencoder_2011new.pdf
第一层全连接层通过反馈得到1600个神经元的误差d,然后组合成5×5×64的形式,这个是误差featuremaps,上采样得到10×10×64的featuremaps,这是卷积层的误差d,一共有64层,每一层需要跟前馈网络的14×14×64分别做卷积,得到一个5×5×64的核的误差d(也可以称为梯度),这样64层分别与前馈网络做卷积就能到64个5×5×64个核函数的误差d,可以参见上图的3,最后要乘以核函数的导数,再通过4求出每一个参数的△W和△b.
cnnbp.m
- <span style="font-family:Times New Roman;font-size:14px;">function net = cnnbp(net, y)</span>
- <div style="text-align: left;"><span style="font-family:Times New Roman;font-size:14px;"><strong style="line-height: 26px; color: rgb(102, 102, 0); background-color: rgb(255, 255, 255);"></strong></span></div><span style="font-family:Times New Roman;font-size:14px;">n = numel(net.layers); % 网络层数
- % error
- net.layers{n}.e = net.layers{n}.a - y;
- % loss function
- % 代价函数是 均方误差
- net.layers{n}.L = 1/2* sum(net.layers{n}.e(:) .^ 2) / size(net.layers{n}.e, 2);
- %% backprop deltas
- % 这里可以参考 UFLDL 的 反向传导算法 的说明
- % 输出层的 灵敏度 或者 残差
- net.layers{8}.od = net.layers{8}.e .* ReluInv(net.layers{8}.a); % output delta
- % 残差 反向传播回 前一层
- net.layers{7}.d = (net.layers{7}.ffW' * net.layers{8}.od) .* ReluInv(net.layers{7}.a); % feature vector delta
- net.layers{6}.d = (net.layers{6}.ffW' * net.layers{7}.d) .* ReluInv(net.layers{6}.a);
- net.layers{5}.fvd = (net.layers{5}.ffW' * net.layers{6}.d);
- % net.layers{l-1}.d = net.layers{l-1}.fvd .* (net.layers{l-1}.o .* (1-net.layers{l-1}));
- % if strcmp(net.layers{n}.type, 'c') % only conv layers has sigm function
- % net.fvd = net.fvd .* (net.fv .* (1 - net.fv));
- % end
- % reshape feature vector deltas into output map style
- sa = size(net.layers{5}.a{1}); % 最后一层特征map的大小。这里的最后一层都是指输出层的前一层
- fvnum = sa(1) * sa(2); % 因为是将最后一层特征map拉成一条向量,所以对于一个样本来说,特征维数是这样
- for j = 1 : numel(net.layers{5}.a) % 最后一层的特征map的个数
- % 在fvd里面保存的是所有样本的特征向量(在cnnff.m函数中用特征map拉成的),所以这里需要重新
- % 变换回来特征map的形式。d 保存的是 delta,也就是 灵敏度 或者 残差
- net.layers{5}.d{j} = reshape(net.layers{5}.fvd(((j - 1) * fvnum + 1) : j * fvnum, :), sa(1), sa(2), sa(3));
- end
- % 对于 输出层前面的层(与输出层计算残差的方式不同)
- for l = (n - 4) : -1 : 1
- if strcmp(net.layers{l}.type, 'c')
- for j = 1 : numel(net.layers{l}.a) % 该层特征map的个数
- % net.layers{l}.d{j} 保存的是 第l层 的 第j个 map 的 灵敏度map。 也就是每个神经元节点的delta的值
- % expand的操作相当于对l+1层的灵敏度map进行上采样。然后前面的操作相当于对该层的输入a进行sigmoid求导
- % 这条公式请参考 Notes on Convolutional Neural Networks
- % for k = 1:size(net.layers{l + 1}.d{j}, 3)
- % net.layers{l}.d{j}(:,:,k) = net.layers{l}.a{j}(:,:,k) .* (1 - net.layers{l}.a{j}(:,:,k)) .* kron(net.layers{l + 1}.d{j}(:,:,k), ones(net.layers{l + 1}.scale)) / net.layers{l + 1}.scale ^ 2;
- % end
- net.layers{l}.d{j} = ReluInv(net.layers{l}.a{j}) .* (expand(net.layers{l + 1}.d{j}, [net.layers{l + 1}.scale net.layers{l + 1}.scale 1]) / net.layers{l + 1}.scale ^ 2);
- end
- elseif strcmp(net.layers{l}.type, 's')
- for i = 1 : numel(net.layers{l}.a) % 第l层特征map的个数
- z = zeros(size(net.layers{l}.a{1}));
- for j = 1 : numel(net.layers{l + 1}.a) % 第l+1层特征map的个数
- z = z + convn(net.layers{l + 1}.d{j}, rot180(net.layers{l + 1}.k{i}{j}), 'full');
- end
- net.layers{l}.d{i} = z;
- end
- end
- end
- %% calc gradients
- % 这里与 Notes on Convolutional Neural Networks 中不同,这里的 子采样 层没有参数,也没有
- % 激活函数,所以在子采样层是没有需要求解的参数的
- for l = 2 : n
- if strcmp(net.layers{l}.type, 'c')
- for j = 1 : numel(net.layers{l}.a)
- for i = 1 : numel(net.layers{l - 1}.a)
- % dk 保存的是 误差对卷积核 的导数
- net.layers{l}.dk{i}{j} = convn(flipall(net.layers{l - 1}.a{i}), net.layers{l}.d{j}, 'valid') / size(net.layers{l}.d{j}, 3);
- end
- % db 保存的是 误差对于bias基 的导数
- net.layers{l}.db{j} = sum(net.layers{l}.d{j}(:)) / size(net.layers{l}.d{j}, 3);
- end
- elseif strcmp(net.layers{l}.type, 'f1')
- net.layers{l-1}.dffW = net.layers{l}.d * net.layers{l-1}.fv'/ size(net.layers{l}.d, 2);
- net.layers{l-1}.dffb = mean(net.layers{l}.d, 2);
- elseif strcmp(net.layers{l}.type, 'f')
- net.layers{l-1}.dffW = net.layers{l}.d * net.layers{l-1}.a'/ size(net.layers{l}.d, 2);
- net.layers{l-1}.dffb = mean(net.layers{l}.d, 2);
- elseif strcmp(net.layers{l}.type, 'o')
- net.layers{l-1}.dffW = net.layers{l}.od * net.layers{l-1}.a'/ size(net.layers{l}.od, 2);
- net.layers{l-1}.dffb = mean(net.layers{l}.od, 2);
- end
- end
- end</span>
6.优化方法选定
优化方法包括梯度法,共轭梯度法,牛顿法,拟牛顿法,但是很多国外大牛都直接用随机批量梯度法,学习率(步长)是按照经验取的,下面给出更新公式,可以结合上面一节。
大家在更新的时候不用管λW这一项,m代表每次批量处理的图像。
7.实验
实验采用的是cifar-10数据库,如下图所示
cnnexample.m
- <span style="font-family:Times New Roman;font-size:14px;">clear all; close all; clc; </span>
- <div style="text-align: left;"><span style="font-family:Times New Roman;font-size:14px;"><strong style="color: rgb(51, 0, 153); line-height: 26px; text-align: center; background-color: rgb(255, 255, 255);"></strong></span></div><span style="font-family:Times New Roman;font-size:14px;">load('traindata.mat');
- load('testdata.mat');
- load('trainlabel.mat');
- load('testlabel.mat');
- train_x = traindata;
- test_x = testdata;
- trainlabel=double(trainlabel);
- trainlabel(trainlabel==0) = 10;
- train_y = full(sparse(trainlabel, 1:50000, 1));
- testlabel=double(testlabel);
- testlabel(testlabel==0) = 10;
- test_y = full(sparse(testlabel, 1:10000, 1));
- %% ex1
- %will run 1 epoch in about 200 second and get around 11% error.
- %With 100 epochs you'll get around 1.2% error
- clear traindata testdata trainlabel testlabel
- cnn.layers = {
- struct('type', 'i','inputmaps',3 ,'inputsize',32) %input layer
- struct('type', 'c', 'outputmaps', 64, 'kernelsize', 5) %convolution layer
- struct('type', 's', 'scale', 2) %sub sampling layer
- struct('type', 'c', 'outputmaps', 64, 'kernelsize', 5) %convolution layer
- struct('type', 's', 'scale', 2) %subsampling layer
- struct('type', 'f1', 'neuron', 1024) %full-connection layer
- struct('type', 'f', 'neuron', 512) %full-connection layer
- struct('type', 'o', 'scale', 10)
- };
- % 这里把cnn的设置给cnnsetup,它会据此构建一个完整的CNNs网络,并返回
- cnn = cnnsetup(cnn, train_x, train_y);
- % 学习率
- opts.alpha = 0.5;
- % 每次挑出一个batchsize的batch来训练,也就是每用batchsize个样本就调整一次权值,而不是
- % 把所有样本都输入了,计算所有样本的误差了才调整一次权值
- opts.batchsize = 200;
- % 训练次数,用同样的样本集。我训练的时候:
- % 1的时候 11.41% error
- % 5的时候 4.2% error
- % 10的时候 2.73% error
- opts.numepochs = 50;
- % 然后开始把训练样本给它,开始训练这个CNN网络
- cnn = cnntrain(cnn, train_x, train_y, opts);
- % 然后就用测试样本来测试
- [er, bad] = cnntest(cnn, test_x, test_y);
- %plot mean squared error
- plot(cnn.rL);
- %show test error
- disp([num2str(er*100) '% error']); </span>
cnntrain.m
- <span style="font-family:Times New Roman;font-size:14px;">function net = cnntrain(net, x, y, opts)
- m = size(x, 4); % m 保存的是 训练样本个数
- numbatches = m / opts.batchsize;
- % rem: Remainder after division. rem(x,y) is x - n.*y 相当于求余
- % rem(numbatches, 1) 就相当于取其小数部分,如果为0,就是整数
- if rem(numbatches, 1) ~= 0
- error('numbatches not integer');
- end
- net.rL = [];
- for i = 1 : opts.numepochs
- % disp(X) 打印数组元素。如果X是个字符串,那就打印这个字符串
- disp(['epoch ' num2str(i) '/' num2str(opts.numepochs)]);
- % tic 和 toc 是用来计时的,计算这两条语句之间所耗的时间
- tic;
- % P = randperm(N) 返回[1, N]之间所有整数的一个随机的序列,例如
- % randperm(6) 可能会返回 [2 4 5 6 1 3]
- % 这样就相当于把原来的样本排列打乱,再挑出一些样本来训练
- kk = randperm(m);
- for l = 1 : numbatches
- % 取出打乱顺序后的batchsize个样本和对应的标签
- batch_x = x(:, :, : ,kk((l - 1) * opts.batchsize + 1 : l * opts.batchsize));
- batch_y = y(:, kk((l - 1) * opts.batchsize + 1 : l * opts.batchsize));
- % 在当前的网络权值和网络输入下计算网络的输出
- net = cnnff(net, batch_x); % Feedforward
- % 得到上面的网络输出后,通过对应的样本标签用bp算法来得到误差对网络权值
- %(也就是那些卷积核的元素)的导数
- net = cnnbp(net, batch_y); % Backpropagation
- % 得到误差对权值的导数后,就通过权值更新方法去更新权值
- net = cnnapplygrads(net, opts);
- if isempty(net.rL)
- net.rL(1) = net.layers{8}.L; % 代价函数值,也就是误差值
- end
- net.rL(end + 1) = 0.99 * net.rL(end) + 0.01 * net.layers{8}.L; % 保存历史的误差值,以便画图分析
- end
- toc;
- end
- end </span>
cnntest.m
- <span style="font-family:Times New Roman;font-size:14px;">function [er, bad] = cnntest(net, x, y)
- % feedforward
- net = cnnff(net, x); % 前向传播得到输出
- % [Y,I] = max(X) returns the indices of the maximum values in vector I
- [~, h] = max(net.o); % 找到最大的输出对应的标签
- [~, a] = max(y); % 找到最大的期望输出对应的索引
- bad = find(h ~= a); % 找到他们不相同的个数,也就是错误的次数
- er = numel(bad) / size(y, 2); % 计算错误率
- end </span>
flipall.m
- <span style="font-family:Times New Roman;font-size:14px;">function X=flipall(X)
- for i=1:ndims(X)
- X = flipdim(X,i);
- end
- end</span>
relu.m
- <span style="font-family:Times New Roman;font-size:14px;">function X = relu(P)
- X=log(1+exp(P));
- end</span>
- <span style="font-family:Times New Roman;font-size:14px;">function reluInv=ReluInv(x)
- reluInv = exp(x)./(1 + exp(x));
- end</span>
- <span style="font-family:Times New Roman;font-size:14px;">function B = expand(A, S)
- if nargin < 2
- error('Size vector must be provided. See help.');
- end
- SA = size(A); % Get the size (and number of dimensions) of input.
- if length(SA) ~= length(S)
- error('Length of size vector must equal ndims(A). See help.')
- elseif any(S ~= floor(S))
- error('The size vector must contain integers only. See help.')
- end
- T = cell(length(SA), 1);
- for ii = length(SA) : -1 : 1
- H = zeros(SA(ii) * S(ii), 1); % One index vector into A for each dim.
- H(1 : S(ii) : SA(ii) * S(ii)) = 1; % Put ones in correct places.
- T{ii} = cumsum(H); % Cumsumming creates the correct order.
- end
- B = A(T{:}); </span>
cnnsetup.m
- <span style="font-family:Times New Roman;font-size:14px;">function net = cnnsetup(net, x, y)
- inputmaps = net.layers{1}.inputmaps;
- % B=squeeze(A) 返回和矩阵A相同元素但所有单一维都移除的矩阵B,单一维是满足size(A,dim)=1的维。
- % train_x中图像的存放方式是三维的reshape(train_x',28,28,60000),前面两维表示图像的行与列,
- % 第三维就表示有多少个图像。这样squeeze(x(:, :, 1))就相当于取第一个图像样本后,再把第三维
- % 移除,就变成了28x28的矩阵,也就是得到一幅图像,再size一下就得到了训练样本图像的行数与列数了
- mapsize = size(squeeze(x(:, :, 1)));
- % 下面通过传入net这个结构体来逐层构建CNN网络
- % n = numel(A)返回数组A中元素个数
- % net.layers中有五个struct类型的元素,实际上就表示CNN共有五层,这里范围的是5
- for l = 1 : numel(net.layers) % layer
- if strcmp(net.layers{l}.type, 's') % 如果这层是 子采样层
- % subsampling层的mapsize,最开始mapsize是每张图的大小28*28
- % 这里除以scale=2,就是pooling之后图的大小,pooling域之间没有重叠,所以pooling后的图像为14*14
- % 注意这里的右边的mapsize保存的都是上一层每张特征map的大小,它会随着循环进行不断更新
- mapsize = floor(mapsize / net.layers{l}.scale);
- for j = 1 : inputmaps % inputmap就是上一层有多少张特征图
- net.layers{l}.b{j} = 0; % 将偏置初始化为0
- end
- end
- if strcmp(net.layers{l}.type, 'c') % 如果这层是 卷积层
- % 旧的mapsize保存的是上一层的特征map的大小,那么如果卷积核的移动步长是1,那用
- % kernelsize*kernelsize大小的卷积核卷积上一层的特征map后,得到的新的map的大小就是下面这样
- mapsize = mapsize - net.layers{l}.kernelsize + 1;
- % 该层需要学习的参数个数。每张特征map是一个(后层特征图数量)*(用来卷积的patch图的大小)
- % 因为是通过用一个核窗口在上一个特征map层中移动(核窗口每次移动1个像素),遍历上一个特征map
- % 层的每个神经元。核窗口由kernelsize*kernelsize个元素组成,每个元素是一个独立的权值,所以
- % 就有kernelsize*kernelsize个需要学习的权值,再加一个偏置值。另外,由于是权值共享,也就是
- % 说同一个特征map层是用同一个具有相同权值元素的kernelsize*kernelsize的核窗口去感受输入上一
- % 个特征map层的每个神经元得到的,所以同一个特征map,它的权值是一样的,共享的,权值只取决于
- % 核窗口。然后,不同的特征map提取输入上一个特征map层不同的特征,所以采用的核窗口不一样,也
- % 就是权值不一样,所以outputmaps个特征map就有(kernelsize*kernelsize+1)* outputmaps那么多的权值了
- % 但这里fan_out只保存卷积核的权值W,偏置b在下面独立保存
- fan_out = net.layers{l}.outputmaps * net.layers{l}.kernelsize ^ 2;
- for j = 1 : net.layers{l}.outputmaps % output map
- % fan_out保存的是对于上一层的一张特征map,我在这一层需要对这一张特征map提取outputmaps种特征,
- % 提取每种特征用到的卷积核不同,所以fan_out保存的是这一层输出新的特征需要学习的参数个数
- % 而,fan_in保存的是,我在这一层,要连接到上一层中所有的特征map,然后用fan_out保存的提取特征
- % 的权值来提取他们的特征。也即是对于每一个当前层特征图,有多少个参数链到前层
- fan_in = inputmaps * net.layers{l}.kernelsize ^ 2;
- for i = 1 : inputmaps % input map
- % 随机初始化权值,也就是共有outputmaps个卷积核,对上层的每个特征map,都需要用这么多个卷积核
- % 去卷积提取特征。
- % rand(n)是产生n×n的 0-1之间均匀取值的数值的矩阵,再减去0.5就相当于产生-0.5到0.5之间的随机数
- % 再 *2 就放大到 [-1, 1]。然后再乘以后面那一数,why?
- % 反正就是将卷积核每个元素初始化为[-sqrt(6 / (fan_in + fan_out)), sqrt(6 / (fan_in + fan_out))]
- % 之间的随机数。因为这里是权值共享的,也就是对于一张特征map,所有感受野位置的卷积核都是一样的
- % 所以只需要保存的是 inputmaps * outputmaps 个卷积核。
- net.layers{l}.k{i}{j} = (rand(net.layers{l}.kernelsize) - 0.5) * 2 * sqrt(6 / (fan_in + fan_out));
- end
- net.layers{l}.b{j} = 0; % 将偏置初始化为0
- end
- % 只有在卷积层的时候才会改变特征map的个数,pooling的时候不会改变个数。这层输出的特征map个数就是
- % 输入到下一层的特征map个数
- inputmaps = net.layers{l}.outputmaps;
- end
- if strcmp(net.layers{l}.type, 'f1')
- fvnum = prod(mapsize) * inputmaps;
- onum = net.layers{l}.neuron;
- net.layers{l-1}.ffb = zeros(onum, 1);
- net.layers{l-1}.ffW = (rand(onum, fvnum) - 0.5) * 2 * sqrt(6 / (onum + fvnum));
- end
- if strcmp(net.layers{l}.type, 'f')
- fvnum = net.layers{l-1}.neuron;
- onum = net.layers{l}.neuron;
- net.layers{l-1}.ffb = zeros(onum, 1);
- net.layers{l-1}.ffW = (rand(onum, fvnum) - 0.5) * 2 * sqrt(6 / (onum + fvnum));
- end
- if strcmp(net.layers{l}.type, 'o')
- fvnum = net.layers{l-1}.neuron;
- onum = net.layers{l}.scale;
- net.layers{l-1}.ffb = zeros(onum, 1);
- net.layers{l-1}.ffW = (rand(onum, fvnum) - 0.5) * 2 * sqrt(6 / (onum + fvnum));
- end
- % fvnum 是输出层的前面一层的神经元个数。
- % 这一层的上一层是经过pooling后的层,包含有inputmaps个特征map。每个特征map的大小是mapsize。
- % 所以,该层的神经元个数是 inputmaps * (每个特征map的大小)
- % prod: Product of elements.
- % For vectors, prod(X) is the product of the elements of X
- % 在这里 mapsize = [特征map的行数 特征map的列数],所以prod后就是 特征map的行*列
- %fvnum = prod(mapsize) * inputmaps;
- % onum 是标签的个数,也就是输出层神经元的个数。你要分多少个类,自然就有多少个输出神经元
- %onum = size(y, 1);
- % 这里是最后一层神经网络的设定
- % ffb 是输出层每个神经元对应的基biases
- %net.ffb = zeros(onum, 1);
- % ffW 输出层前一层 与 输出层 连接的权值,这两层之间是全连接的
- %net.ffW = (rand(onum, fvnum) - 0.5) * 2 * sqrt(6 / (onum + fvnum));
- end</span>
数据准备:整个数据为4-D的double型数据
每一维数据是这样的,前2维代表每一帧图像的大小,如文章中指的32×32,第3维代表输入图片的通道,一共为3通道,那么前3维就组成了一个样本,第4维代表样本的数量。这样就生成了训练集。测试集也一样。
数据的标签:
trainlabel=double(trainlabel);
trainlabel(trainlabel==0) = 10;
train_y = full(sparse(trainlabel, 1:50000, 1));
每一类分别给出相应的标签,如1,2,3,…,n








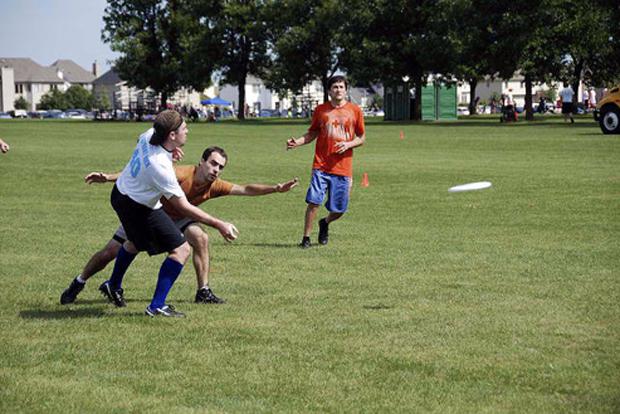

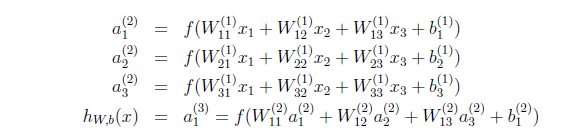

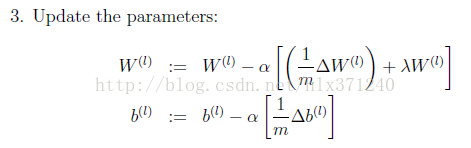















 606
606

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








