[图的搜索]4.图解贝尔曼-福特算法及其代码演示

本文链接：https://blog.csdn.net/jhghuhbb/article/details/139270190

贝尔曼-福特算法
贝尔曼-福特（Bellman-Ford）算法是一种在图中求解最短路径问题的算法。最短路径问题就是在加权图指定了起点和终点的前提下，寻找从起点到终点的路径中权重总和最小的那条路径。

图解

01

这里我们设A为起点、G为终点，来讲解贝尔曼-福特算法。

02

首先设置各个顶点的初始权重：起点为0，其他顶点为无穷大（∞）。这个权重表示的是从A到该顶点的最短路径的暂定距离。随着计算往下进行，这个值会变得越来越小，最终收敛到正确的数值。

03

从所有的边中选出一条边，此处选择了连接A-B的边。然后，分别计算这条边从一端到另一端的权重，计算方法是“顶点原本的权重+边的权重”。只要按顺序分别计算两个方向的权重即可，从哪一端开始都没有问题。此处我们选择按顶点权重从小到大的方向开始计算。

04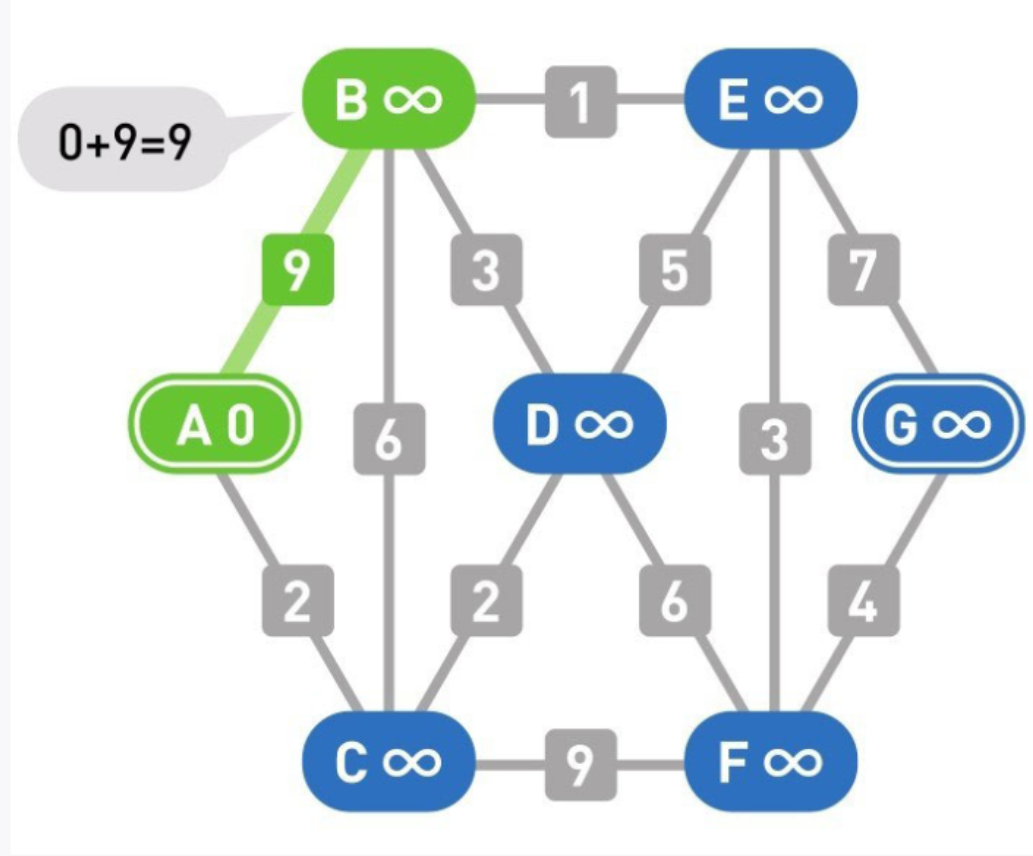

A的权重小于B，因此先计算从A到B的权重。A的权重是0，边A-B的权重是9，因此A到B的权重是0+9=9。

05

如果计算结果小于顶点的值，就更新这个值。顶点B的权重是无穷大，比9大，所以把它更新为9。更新时需要记录计算的是从哪个顶点到该顶点的路径。

06

接下来计算从B到A的权重。B的权重为9，从B到A的权重便为9+9=18。与顶点A现在的值0进行比较，因为现在的值更小，所以不更新。

07

对所有的边都执行同样的操作。在执行顺序上没有特定要求，此处我们选择从靠近左侧的边开始计算。先选出一条边……

08

数值更新了，顶点C的权重变成了2。

09

同样地，再选出一条边……

权重又更新了。此时就能看出，从顶点A前往顶点B时，比起从A直达B，在C中转一次的权重更小。

11

接着对所有的边进行更新操作。

12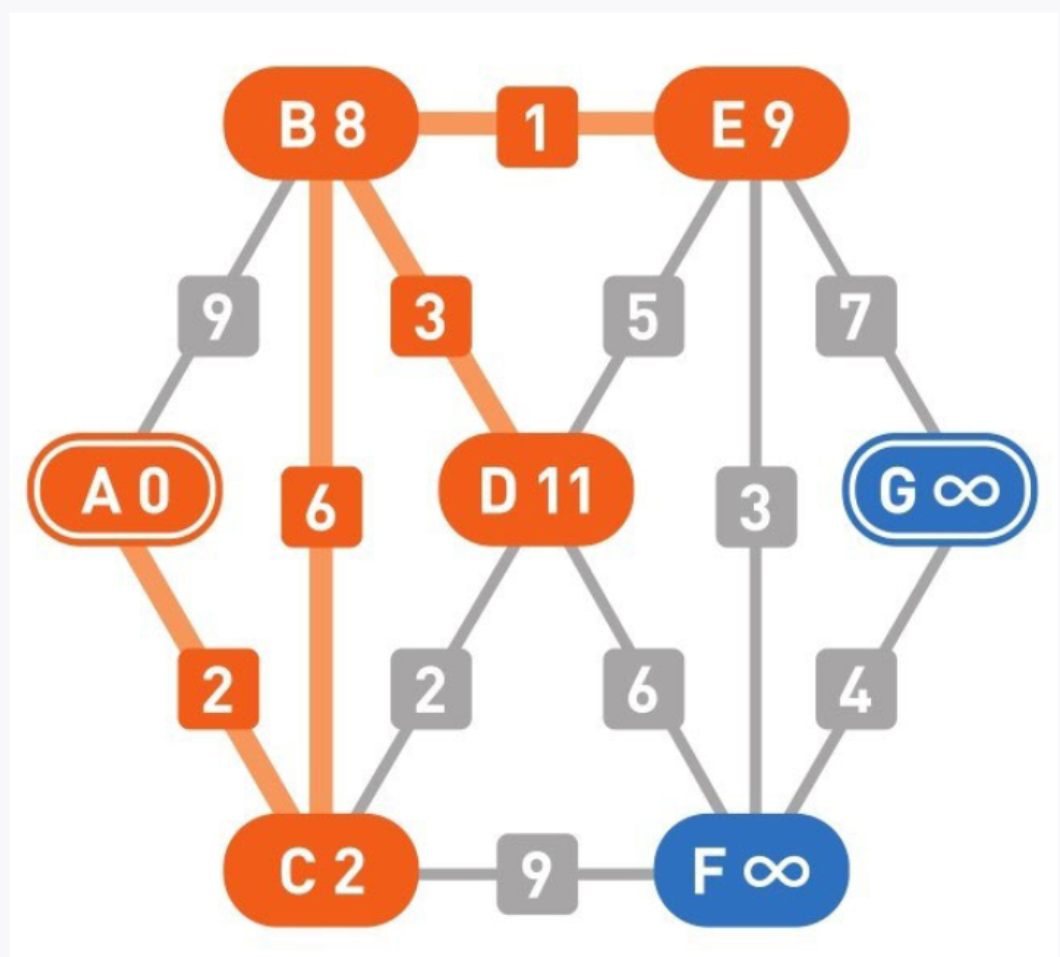

更新边B-D和边B-E。

13
更新边C-D和边C-F。

14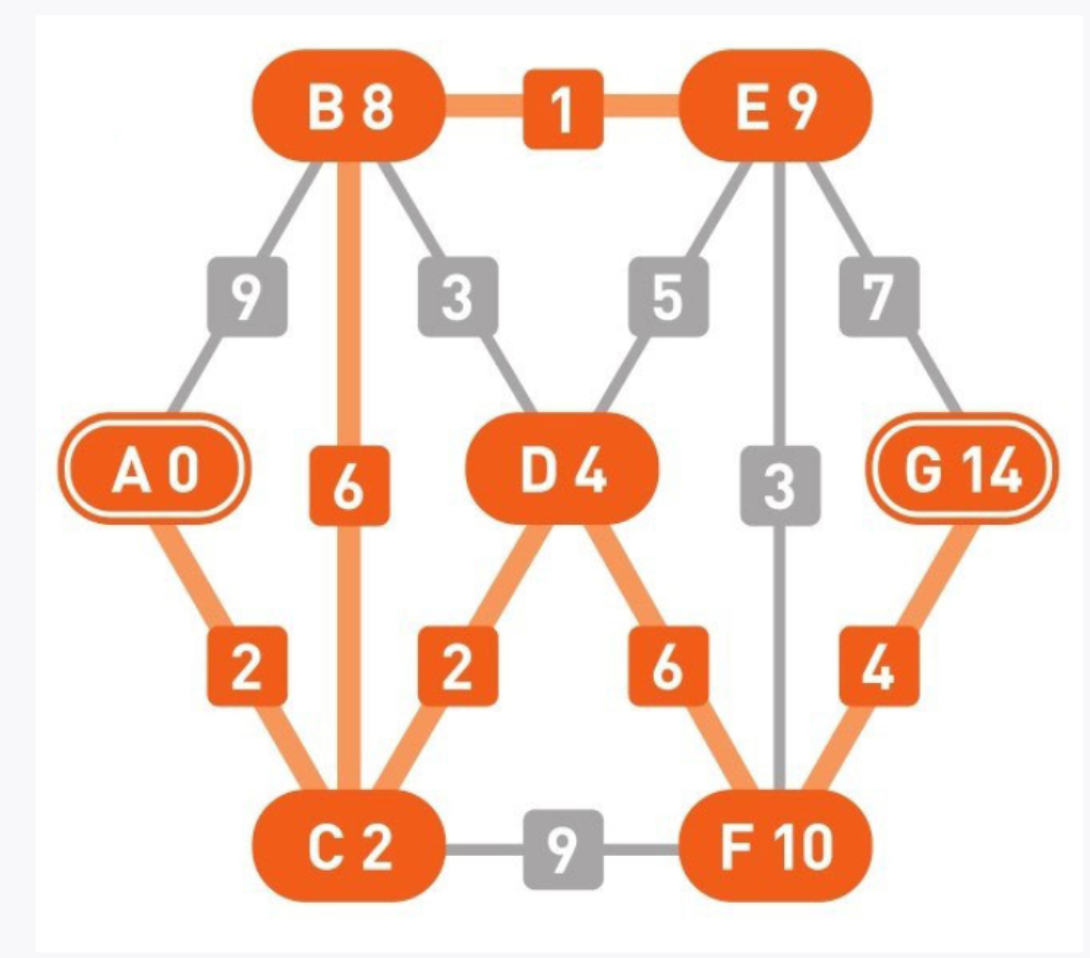

更新完所有的边后，第1轮更新就结束了。接着，重复对所有边的更新操作，直到权重不能被更新为止。

15

第2轮更新也结束了。顶点B的权重从8变成了7，顶点E的权重从9变成了8。接着，再执行一次更新操作。

16

第3轮更新结束，所有顶点的权重都不再更新，操作到此为止。算法的搜索流程也就此结束，我们找到了从起点到其余各个顶点的最短路径。

17

根据搜索结果可知，从起点A到终点G的最短路径是A-C-D-F-G，权重为14。

解说
将图的顶点数设为n、边数设为m，我们来思考一下贝尔曼-福特算法的时间复杂度是多少。该算法经过n轮更新操作后就会停止，而在每轮更新操作中都需要对各个边进行1次确认，因此1轮更新所花费的时间就是O（m），整体的时间复杂度就是O（nm）。
为了便于说明，前面的讲解以无向图为例，但在有向图中同样可以求解最短路径问题。选出一条边并计算顶点的权重时，无向图中的计算如前文步骤03～06所示，两个方向都要计算，而在有向图中只按照边所指向的那个方向来计算就可以了。

补充说明
计算最短路径时，边的权重代表的通常都是时间、距离或者路费等，因此基本都是非负数。不过，即便权重为负，贝尔曼-福特算法也可以正常运行。
但是，如果在一个闭环中边的权重总和是负数，那么只要不断遍历这个闭环，路径的权重就能不断减小，也就是说根本不存在最短路径。遇到这种对顶点进行n次更新操作后仍能继续更新的情况，就可以直接认定它“不存在最短路径”。

小知识
贝尔曼-福特算法的名称取自其创始人理查德·贝尔曼和莱斯特·福特的名字。贝尔曼也因为提出了该算法中的一个重要分类“动态规划”而被世人所熟知。

步骤：

对图中的每条边进行遍历；
对于每条边的两个端点节点，比较从起始节点到第一个节点的距离加上边的权重，与从起始节点到第二个节点的距离的大小；
如果从起始节点到第一个节点的距离加上边的权重小于从起始节点到第二个节点的距离，则更新从起始节点到第二个节点的距离为从起始节点到第一个节点的距离加上边的权重；
不断重复以上步骤，直到没有需要更新的节点，或执行了足够次数的松弛操作。

演示：

def bellman_ford(graph, start):
    # 初始化距离字典，起始点到各点的距离
    distance = {node: float('inf') for node in graph}
    distance[start] = 0

    # 对图中的所有边进行松弛操作
    for _ in range(len(graph) - 1):
        for node in graph:
            for neighbor, weight in graph[node].items():
                if distance[node] + weight < distance[neighbor]:
                    distance[neighbor] = distance[node] + weight

    # 检查负权环
    for node in graph:
        for neighbor, weight in graph[node].items():
            if distance[node] + weight < distance[neighbor]:
                print("图中包含负权环，无最短路径")
                return

    return distance

# 示例图的邻接表表示
graph = {
    'A': {'B': 9, 'C': 2},
    'B': {'A': 9, 'C': 6, 'D': 3, 'E': 1},
    'C': {'A': 2, 'B': 6, 'D': 2, 'F': 9},
    'D': {'B': 3, 'C': 2, 'E': 5, 'F': 6},
    'E': {'B': 1, 'D': 5, 'F': 3, 'G': 7},
    'F': {'C': 9, 'D': 6, 'E': 3, 'G': 4},
    'G': {'E': 7, 'F': 4}
}

# 从节点'A'开始进行贝尔曼-福特算法
result = bellman_ford(graph, "A")
print(result)

结果：

{'A': 0, 'B': 7, 'C': 2, 'D': 4, 'E': 8, 'F': 10, 'G': 14}

———————————————————————————————————————————

文章来源:书籍《我的第一本算法书》

书籍链接:

我的第一本算法书 (豆瓣) (douban.com)

作者：宫崎修一石田保辉

出版社：人民邮电出版社

ISBN：9787115495242

本篇文章仅用于学习和研究目的，不会用于任何商业用途。引用书籍《我的第一本算法书》的内容旨在分享知识和启发思考，尊重原著作者宫崎修一和石田保辉的知识产权。如有侵权或者版权纠纷，请及时联系作者。
———————————————————————————————————————————