Leetcode 1015. 可被 K 整除的最小整数

Leetcode 1015. 可被 K 整除的最小整数

假设这个数是$k$，如果$K$满足要求，那么必定存在等式$nK=111\cdots 111$，我们的思路是如何求解这个$n$。

在这里，我们令$n=n_0\times 1+n_1\times 10+n_2\times 100+\dots ++n_c\times 10^c$，即序列$<n_c{n}_{c-1}\dots n_1{n}_0>$就是$n$的每一位。

第一步

我们模拟竖式乘法的过程，乘积$nK$如果最后一位等于$1$，那么乘积$n_{0}K$的最后一位也必然等于1。（这里和下文的最后一位都是指的最低位）此时我们就需要搬出我们小学二年级学习的九九乘法表了。

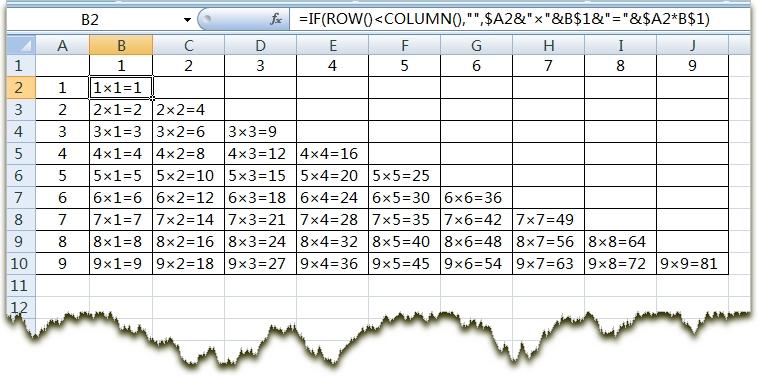
观察上表，我们发现只有当$K$的最后一位为$1,3,7,9$的时候，才有对应的$n_0$存在，即下表：

K的最后一位	$n_0$	乘积
1	1	1
3	7	21
7	3	21
9	9	81

除此之外我们找不到其他的组合了。因此我们检查$K$的最低位$K_0$是否为$1,3,7,9$，如果是那么必定有解，如果不是那么必定无解。（下文解释为什么必定有解）

第二步

到这里，乘积$nK$的最后一位已经是$1$了，我们再令下一位也是$1$。此时决定乘积$nK$倒数第二位结果的是$n_1$。但是和第一步不同的是，此时决定乘积$nK$倒数第二位结果的还有上一步的乘积，如下图：

例如上图，$K=7$，乘积$nK$的倒数第二位的结果应该是$7\times n_1$的最后一位加上$3\times 7$的该位上的结果$2$，那么$n_1$应该是几呢，我们知道$7\times n_1$的最后一位应该是$9$，$9+2=11$正好落$1$进$1$，那么$n_1$是几，$n_1\times 7$的最后一位能是$9$呢，我们继续查表，发现仅有$7\times 7=49$，最后一位才是9，因此$n_1=7$。

剩下过程就是继续这个操作，一直到不需要再乘下去，乘积的每一位都是$1$结束。

第三步

那就是证明必定有解。调节每一位都是由$n_i\times K_0$得到的，又因为$K_0$只能是$1,3,7,9$，我们看看乘法表，发现凡是和$1,3,7,9$相乘的乘积最后一位正好覆盖了从$0$到$9$的所有数字（0就是和0乘），必定能够调节任何数字，使该位的结果为$1$，因此必定有解。

代码

class Solution
{
public:
    int arr[10][10];

    int smallestRepunitDivByK(int K)
    {
        // 1,3,7,9
        int good[] = {1, 3, 7, 9};

        // 构造乘法表，arr[i][j]表示K的最后一位是i，我想要最后一位结果是j的因子
        for (int i = 0; i < 4; i++)
        {
            for (int k = 0; k <= 9; k++)
            {
                int ans = good[i] * k;

                arr[good[i]][ans % 10] = k;
            }
        }

        // 取K的最后一位
        int tail = K % 10;

        // 不是1,3,7,9直接输出-1
        if (tail != 1 && tail != 3 && tail != 7 && tail != 9)
        {
            return -1;
        }

        // sum 表示当前乘积的和
        int sum = 0;
        int cnt = 0;
        // 如果sum=1，不需要任何操作，直接把sum落下来即可
        while (sum != 1)
        {
            // sum最后一位肯定是1，扔掉让加和的时候能对齐
            sum /= 10;
            // 取上一次的结果
            int t = sum % 10;
            // 需要加上的数字才能令该位等于1，例如t等于0，需要1才能令1+0=1；t=3，需要8才能令3+8=11
            int need = (11 - t) % 10;
            // 取得ni
            int fact = arr[tail][need];
            // 相乘累加结果
            sum += K * fact;
            cnt++;
        }
        return cnt;
    }
};

扩展

1. 如果要求出$n$，直接拼接$fact$即可
2. 此题要求1的位数最小，那么有没有不是最小的情况呢？答案是肯定的，当$sum=1$的时候我们不停止，继续该过程。此时对应的$NK=111\cdots 111$，$N$的形式一定是$n0n0n0n0n\dots$，即$n$和$0$交替出现。