带挂牵引车前向运动模型推导及仿真实现

1.序言

牵引车-半挂车的车辆结构与普通的车辆相比增加了一个半挂车，它们之间通过鞍座相连接，为了分析半挂牵引车运动过程中的位姿和状态，本文将基于车辆的机械结构建立对应的运动学模型，该模型基于以下假设：

• 车辆行驶过程中，道路平坦且无凸凹；
• 车辆低速行驶，且运行过程中车身无侧倾和俯仰运动；
• 车辆行驶过程中，轮胎无形变，无侧向滑动，且无侧向力；
• 牵引车和半挂车均满足阿克曼转向几何原理；
• 牵引车与半挂车不会发现折叠。

2. 运动学模型及推导

牵引车带挂前向运动是开环稳定的，其对应的自行车模型如下所示：

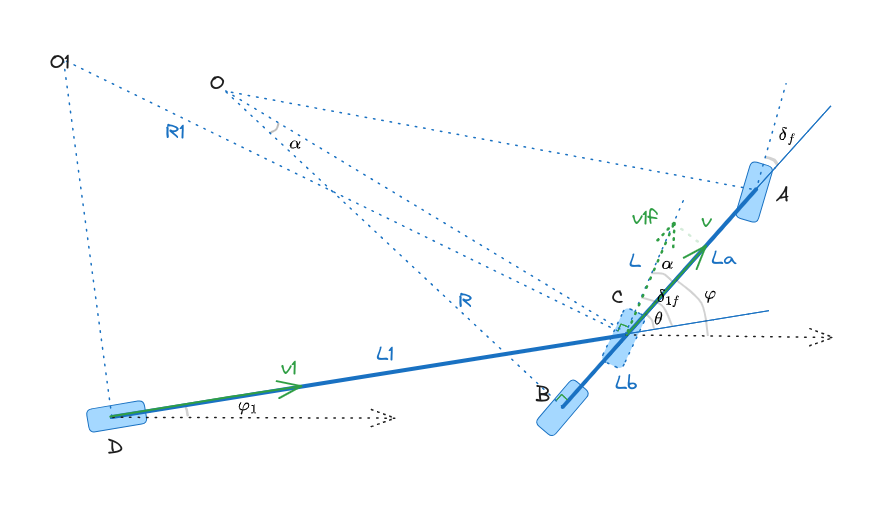
其中：

• $A$：牵引车的前轮中心点，其坐标为$(x_f,y_f)$；
• $B$：牵引车后轮中心点，其坐标为$(x_r,y_r)$；
• $C$：牵引车与半挂车的铰接点，也是半挂车的等效前轮中心点，其坐标为$(x_{1f},y_{1f})$；
• $D$：半挂车后轮中心点，其坐标为$(x_{1r},y_{1r})$；
• $L$：牵引车的轴距；
• $L_a$：铰接点$C$到$A$的距离；
• $L_b$：铰接点$C$到$B$的距离；
• $L1$：半挂车的轴距；
• ${\delta }_f$：牵引车前轮转角；
• ${\delta }_{1f}$：半挂车虚拟前轮转角；
• $\phi$：牵引车航向角；
• ${\phi }_1$：半挂车的航向角；
• $\theta$：铰接角，即牵引车与半挂车的航向的夹角；
• $v$：牵引车的纵向速度；
• $v_1$：半挂车的纵向速度；
• $v_{1f}$：挂车虚拟前轮速度；
• $\alpha$：挂车虚拟前轮与牵引车航向的夹角。

结合我们前面车辆运动学方程推导和代码实现的推导，可得牵引车的运动学模型如下
$$\{\begin{array}{l}\dot{x_r}=v\cos \phi \\ \dot{y_r}=v\sin \phi \\ \dot{\phi }=\frac{v\tan {\delta }_f}{L}\end{array}\text{\hspace{1em}(1)}$$
对于半挂车我们也把其等效为自行车模型，则其也有
$$\{\begin{array}{l}\dot{x_{1r}}=v_1\cos {\phi }_1\\ \dot{y_{1r}}=v_1\sin {\phi }_1\\ \dot{{\phi }_1}=\frac{v_1\tan {\delta }_{1f}}{L_1}\end{array}\text{\hspace{1em}(2)}$$
根据图中几何关系，可得挂车虚拟前轮速度$v_{1f}$与纵向速度$v_1$的关系有
$$v_1=v_{1f}\cos {\delta }_{1f}=v_{1f}\cos (\alpha +\theta )\text{\hspace{1em}(3)}$$
其中$\theta =\phi -{\phi }_1$。

由于牵引车与挂车是通过挢接点进行动力牵引的，所以半挂车虚拟前轮的速度与牵引车的纵向速度存在以下等式关系：
$$v_{1f}=\frac{v}{\cos \alpha }\text{\hspace{1em}(4)}$$
由公式3、4可得
$$v_1=v_{1f}\cos {\delta }_{1f}=\frac{v\cos (\alpha +\theta )}{\cos \alpha }\text{\hspace{1em}(5)}$$
结合上图和阿克曼转向原理可得
$$\begin{gathered} R=\frac{L}{\tan {\delta }_f} \\ {R}_1=\frac{L_1}{\tan {\delta }_{1f}}\text{\hspace{1em}(6)} \end{gathered}$$

注：具体推导可参考历史文章：车辆运动学方程推导和代码实现

由图中的几何关系可得
$$\tan \alpha =\frac{L_b}{R}=\frac{L_b\tan {\delta }_f}{L}\text{\hspace{1em}(7)}$$
由5、7可得
$$v_1=\frac{v\cos (\alpha +\theta )}{\cos \alpha }=v(\cos \theta -\tan \alpha \sin \theta )=v(\cos \theta -\frac{L_b\tan {\delta }_f}{L}\sin \theta )\text{\hspace{1em}(8)}$$
由2、7和8可得
$$\begin{array}{c}\begin{array}{rl}\dot{{\phi }_1}& =\frac{v_1\tan {\delta }_{1f}}{L_1}\\ & =\frac{v(\cos \theta -\frac{L_b\tan {\delta }_f}{L}\sin \theta )}{L_1}\tan {\delta }_{1f}\\ & =\frac{v(\cos \theta -\frac{L_b\tan {\delta }_f}{L}\sin \theta )}{L_1}\frac{\tan \phi +\tan \theta }{1-\tan \phi \tan \theta }\\ & =\frac{v(\cos \theta -\frac{L_b\tan {\delta }_f}{L}\sin \theta )}{L_1}\frac{\frac{L_b\tan {\delta }_f}{L}+\tan \theta }{1-\frac{L_b\tan {\delta }_f}{L}\tan \theta }\\ & =\frac{v(\cos \theta -\frac{L_b\tan {\delta }_f}{L}\sin \theta )}{L_1}\frac{L_b\tan {\delta }_f+L\tan \theta }{L-L_b\tan {\delta }_f\tan \theta }\\ & =\frac{v}{L_1}(\sin \theta +\frac{L_b\tan {\delta }_f\cos \theta }{L})\end{array}\end{array}\text{\hspace{1em}(9)}$$

结合上图几何关系，可得挂车的后轴中心坐标为
$$\{\begin{array}{l}{x}_{1r}=x_r+L_b\cos \phi -L_1\cos {\phi }_1\\ y_{1r}=y_r+L_b\sin \phi -L\sin {\phi }_1\end{array}\text{\hspace{1em}(10)}$$
综上，带挂牵引车的运动学模型方程如下所示：

$$\{\begin{array}{l}\dot{x_r}=v\cos \phi \\ \dot{y_r}=v\sin \phi \\ \dot{\phi }=\frac{v\tan {\delta }_f}{L}\\ \dot{{\phi }_1}=\frac{v}{L_1}(\sin \theta +\frac{L_b\tan {\delta }_f\cos \theta }{L})\\ \theta =\phi -{\phi }_1\end{array}\text{\hspace{1em}(11)}$$

3. 代码实现

semi_truck_fwd_model.py

import math
import matplotlib.pyplot as plt
import numpy as np
import imageio.v2 as imageio

class VehicleParamInfo:
    # 牵引车（车头）
    L = 3.0  # 轴距
    W = 2.0  # 宽度
    LF = 3.8  # 后轴中心到车头距离
    LB = 0.8  # 后轴中心到车尾距离
    MAX_STEER = 0.6  # 最大前轮转角
    TR = 0.5  # 轮子半径
    TW = 0.5  # 轮子宽度
    WD = W  # 轮距
    LENGTH = LB + LF  # 车辆长度
    La = 2.7  # 铰接点到牵引车前轴中心的距离
    Lb = 0.3  # 铰接点到牵引车后轴中心的距离
    # 挂车
    L1 = 7  # 挂车轴距
    LF1 = 8.0  # 挂车后轴中心到车头距离
    LB1 = 1.0  # 挂车后轴中心到车尾距离

def normalize_angle(angle):
    a = math.fmod(angle + np.pi, 2 * np.pi)
    if a < 0.0:
        a += (2.0 * np.pi)
    return a - np.pi

class Vehicle:
    def __init__(self, x=0.0, y=0.0, yaw=0.0, v=0.0, dt=0.1, vehicle_param_info=VehicleParamInfo):
        # 牵引车
        self.steer = 0
        self.x = x
        self.y = y
        self.yaw = yaw
        self.v = v
        self.dt = dt
        self.vehicle_param_info = vehicle_param_info
        self.x_front = self.x + self.vehicle_param_info.L * math.cos(self.yaw)
        self.y_front = self.y + self.vehicle_param_info.L * math.sin(self.yaw)
        # 挂车
        self.yaw1 = yaw
        self.x_front1 = self.x + self.vehicle_param_info.Lb * math.cos(self.yaw)
        self.y_front1 = self.y + self.vehicle_param_info.Lb * math.sin(self.yaw)
        self.x1 = self.x_front1 - self.vehicle_param_info.L1 * math.cos(self.yaw1)
        self.y1 = self.y_front1 - self.vehicle_param_info.L1 * math.sin(self.yaw1)

    def update(self, a, delta, max_steer=None):
        if max_steer is None:
            max_steer = self.vehicle_param_info.MAX_STEER
        delta = np.clip(delta, -max_steer, max_steer)
        self.steer = delta
        hitchAngle = normalize_angle(self.yaw-self.yaw1)

        self.x += self.v * math.cos(self.yaw) * self.dt
        self.y += self.v * math.sin(self.yaw) * self.dt
        self.x_front = self.x + self.vehicle_param_info.L * math.cos(self.yaw)
        self.y_front = self.y + self.vehicle_param_info.L * math.sin(self.yaw)

        self.x_front1 = self.x + self.vehicle_param_info.Lb * math.cos(self.yaw)
        self.y_front1 = self.y + self.vehicle_param_info.Lb * math.sin(self.yaw)
        self.x1 = self.x_front1 - self.vehicle_param_info.L1 * math.cos(self.yaw1)
        self.y1 = self.y_front1 - self.vehicle_param_info.L1 * math.sin(self.yaw1)

        self.yaw += self.v / self.vehicle_param_info.L * math.tan(delta) * self.dt
        self.yaw = normalize_angle(self.yaw)

        self.v += a * self.dt
        self.yaw1 += self.v / self.vehicle_param_info.L1 * (
                    math.sin(hitchAngle) + self.vehicle_param_info.Lb * math.tan(self.steer) * math.cos(
                hitchAngle) / self.vehicle_param_info.L) * self.dt
        self.yaw1 = normalize_angle(self.yaw1)
def draw_vehicle_trailer(x, y, yaw,x1, y1, yaw1, steer, ax, vehicle_param_info=VehicleParamInfo, color='black'):

    vehicle_outline = np.array([
        [-vehicle_param_info.LB, vehicle_param_info.LF, vehicle_param_info.LF, -vehicle_param_info.LB, -vehicle_param_info.LB],
        [vehicle_param_info.W / 2, vehicle_param_info.W / 2, -vehicle_param_info.W / 2, -vehicle_param_info.W / 2, vehicle_param_info.W / 2]
    ])
    vehicle_outline1 = np.array([
        [-vehicle_param_info.LB1, vehicle_param_info.LF1, vehicle_param_info.LF1, -vehicle_param_info.LB1,
         -vehicle_param_info.LB1],
        [vehicle_param_info.W / 2, vehicle_param_info.W / 2, -vehicle_param_info.W / 2, -vehicle_param_info.W / 2,
         vehicle_param_info.W / 2]
    ])

    wheel = np.array([
        [-vehicle_param_info.TR, vehicle_param_info.TR, vehicle_param_info.TR, -vehicle_param_info.TR, -vehicle_param_info.TR],
        [vehicle_param_info.TW / 2, vehicle_param_info.TW / 2, -vehicle_param_info.TW / 2, -vehicle_param_info.TW / 2, vehicle_param_info.TW / 2]
    ])

    rr_wheel = wheel.copy()  # 右后轮
    rl_wheel = wheel.copy()  # 左后轮
    fr_wheel = wheel.copy()  # 右前轮
    fl_wheel = wheel.copy()  # 左前轮
    rr_wheel1 = wheel.copy()  # 挂车右后轮
    rl_wheel1 = wheel.copy()  # 挂车左后轮
    rr_wheel[1, :] += vehicle_param_info.WD / 2
    rl_wheel[1, :] -= vehicle_param_info.WD / 2
    rr_wheel1[1, :] += vehicle_param_info.WD / 2
    rl_wheel1[1, :] -= vehicle_param_info.WD / 2

    # 前轮旋转
    rot1 = np.array([
        [np.cos(steer), -np.sin(steer)],
        [np.sin(steer), np.cos(steer)]
    ])
    # yaw旋转矩阵
    rot2 = np.array([
        [np.cos(yaw), -np.sin(yaw)],
        [np.sin(yaw), np.cos(yaw)]
    ])

    # yaw1旋转矩阵
    rot3 = np.array([
        [np.cos(yaw1), -np.sin(yaw1)],
        [np.sin(yaw1), np.cos(yaw1)]
    ])

    fr_wheel = np.dot(rot1, fr_wheel)
    fl_wheel = np.dot(rot1, fl_wheel)
    fr_wheel += np.array([[vehicle_param_info.L], [-vehicle_param_info.WD / 2]])
    fl_wheel += np.array([[vehicle_param_info.L], [vehicle_param_info.WD / 2]])

    fr_wheel = np.dot(rot2, fr_wheel)
    fr_wheel[0, :] += x
    fr_wheel[1, :] += y
    fl_wheel = np.dot(rot2, fl_wheel)
    fl_wheel[0, :] += x
    fl_wheel[1, :] += y
    rr_wheel = np.dot(rot2, rr_wheel)
    rr_wheel[0, :] += x
    rr_wheel[1, :] += y
    rl_wheel = np.dot(rot2, rl_wheel)
    rl_wheel[0, :] += x
    rl_wheel[1, :] += y
    vehicle_outline = np.dot(rot2, vehicle_outline)
    vehicle_outline[0, :] += x
    vehicle_outline[1, :] += y

    rr_wheel1 = np.dot(rot3, rr_wheel1)
    rr_wheel1[0, :] += x1
    rr_wheel1[1, :] += y1
    rl_wheel1 = np.dot(rot3, rl_wheel1)
    rl_wheel1[0, :] += x1
    rl_wheel1[1, :] += y1
    vehicle_outline1 = np.dot(rot3, vehicle_outline1)
    vehicle_outline1[0, :] += x1
    vehicle_outline1[1, :] += y1

    ax.plot(fr_wheel[0, :], fr_wheel[1, :], color)
    ax.plot(rr_wheel[0, :], rr_wheel[1, :], color)
    ax.plot(fl_wheel[0, :], fl_wheel[1, :], color)
    ax.plot(rl_wheel[0, :], rl_wheel[1, :], color)
    ax.plot(rr_wheel1[0, :], rr_wheel1[1, :], color)
    ax.plot(rl_wheel1[0, :], rl_wheel1[1, :], color)
    ax.plot(vehicle_outline[0, :], vehicle_outline[1, :], color)
    ax.plot(vehicle_outline1[0, :], vehicle_outline1[1, :], color)

if __name__ == "__main__":
    vehicle = Vehicle(x=0.0, y=0.0, yaw=np.pi/3, v=0.0, dt=0.1)
    vehicle.v = 1
    trajectory_x = []
    trajectory_y = []
    trailer_trajectory_x = []
    trailer_trajectory_y = []
    fig, ax = plt.subplots()
    image_list = []  # 存储图片
    for i in range(1120):
        ax.cla()
        ax.set_aspect('equal', adjustable='box')
        delta = -np.pi / 10.0 if i > 560 else np.pi / 10.0
        vehicle.update(0,  delta)
        draw_vehicle_trailer(vehicle.x, vehicle.y, vehicle.yaw, vehicle.x1, vehicle.y1, vehicle.yaw1, vehicle.steer, ax)
        trajectory_x.append(vehicle.x)
        trajectory_y.append(vehicle.y)
        trailer_trajectory_x.append(vehicle.x1)
        trailer_trajectory_y.append(vehicle.y1)
        ax.plot(trajectory_x, trajectory_y, 'blue')
        ax.plot(trailer_trajectory_x, trailer_trajectory_y, 'green')
        ax.set_xlim(-22, 20)
        ax.set_ylim(-20, 18)
        plt.pause(0.001)
    #     plt.savefig("temp.png")
    #     i += 1
    #     if (i % 30) == 0:
    #         image_list.append(imageio.imread("temp.png"))
    #
    # imageio.mimsave("display.gif", image_list, duration=0.2)

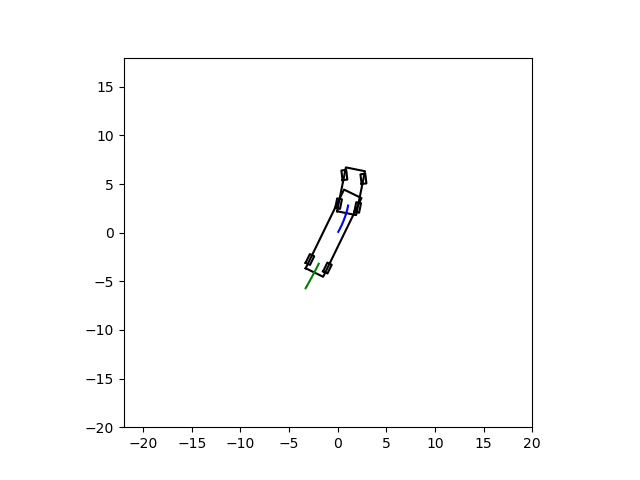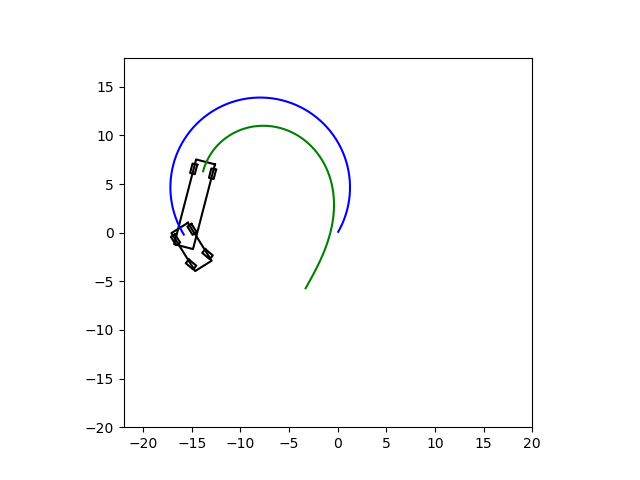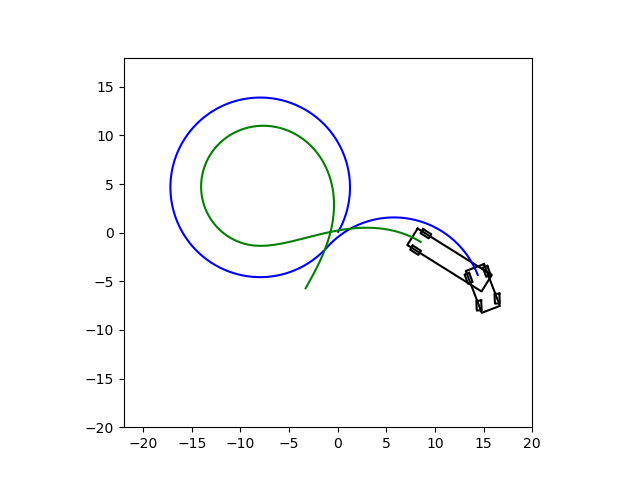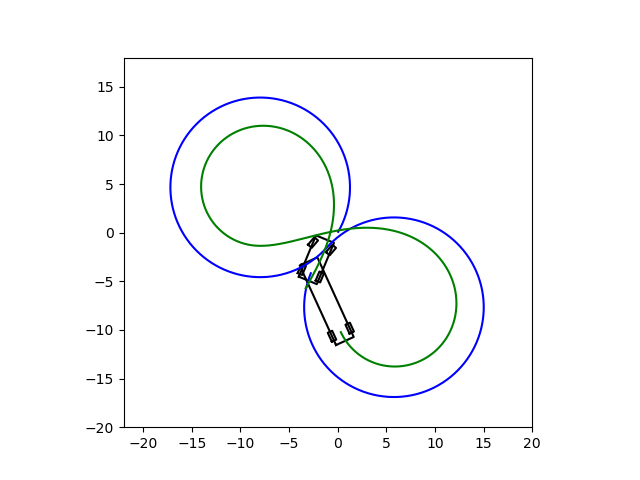
运行效果如下：

参考文献

[1]贾生超.半挂牵引车自动泊车路径规划与运动控制方法研究[D].燕山大学,2023.