最大连续子序列和（java）

最大连续子序列和

最大连续子序列和是一个常见的面试题，也是算法中经典的一个问题。作为总结，今天就从最简单的暴力求解，写道目前能达到最好的线性时间复杂度的算法。

问题描述：找出一个整型数组中的最大连续子序列的和
测试用例：int[] a = { 1, -3, 7, 8, -4, 12, -10, 6 };
输出：23

//即最大连续子序列和是 7 + 8 - 4+ 12 = 23

1、O（n^3）的暴力求解

/**
     * 求解思路：暴力枚举所有的可能性，得出最后的结果
     *  时间复杂度为O(n^3) 
     * 相当糟糕的一种解题思路，只能用于参考，没有实用价值
     */
    public static int maxSubSum1(int[] a) {
        int maxSum = 0;

        for (int i = 0; i < a.length; i++) {
            for (int j = i; j < a.length; j++) {
                int tempSum = 0;

                for (int k = i; k <= j; k++) {
                    tempSum += a[k];
                }

                if (tempSum > maxSum) {
                    maxSum = tempSum;
                }

            }
        }
        return maxSum;
    }

2、O（n^2）的暴力求解改进算法

/**
     * 求解思路：稍稍看一眼暴力求解的思路没，就会发现，用k去逐个标记其实是一个多余的做法
     * 所以，在此进行修改代码，减少一个for循环
     * 时间复杂度：O(n^2)
     * 这个算法比暴力求解稍微好了点儿，但是依然效率糟糕，没有实用价值
     */
    public static int maxSubSum2(int[] a) {
        int maxSum = 0;

        for (int i = 0; i < a.length; i++) {
            int tempSum = 0;

            for (int j = i; j < a.length; j++) {
                tempSum += a[j];

                if (tempSum > maxSum)
                    maxSum = tempSum;
            }
        }
        return maxSum;
    }

3、O(NlogN)的分治策略算法

/**
     * 解题思路：在一个数组中要找到最大连续子序列和，这个和要么出现在左半部分，要么出先在右半部分
     *          要么出现在横跨两部分之间
     * 时间复杂度:O(NlogN)
     * 这个算法就有一定的实用价值，虽然在效率上还是逊色于线性复杂度的算法
     */

    public static int maxSubSum3(int[] a) {
        return subSum3(a, 0, a.length - 1);
    }

    private static int subSum3(int[] a, int left, int right) {
        if (left == right)
            if (a[left] > 0)
                return a[left];
            else
                return 0;

        int center = (left + right) / 2;
        int maxLeftSum = subSum3(a, left, center);
        int maxRightSum = subSum3(a, center + 1, right);

        int maxLeftBorderSum = 0, leftBorderSum = 0;
        for (int i = center; i >= left; i--) {
            leftBorderSum += a[i];
            if (leftBorderSum > maxLeftBorderSum)
                maxLeftBorderSum = leftBorderSum;
        }

        int maxRightBorderSum = 0, rightBorderSum = 0;
        for (int i = center + 1; i <= right; i++) {
            rightBorderSum += a[i];
            if (rightBorderSum > maxRightBorderSum)
                maxRightBorderSum = rightBorderSum;
        }

        return Math.max(Math.max(maxLeftSum, maxRightSum), maxLeftBorderSum + maxRightBorderSum);

    }

4、O(N)的优化算法

/**
     * 求解思路：在算法一和算法二中，我们一直在用两个变量来标识遍历数组
     *  j代表当前序列的重点，i代表当前序列的起点
     *  如果我们只是单纯的想知道最大连续子序列的和，而不想知道最佳连续子序列的起点和终点的话
     *  那么这个i是完全可以被优化掉的
     * 时间复杂度：O(N)
     * 这个算法就是我们经常采用的算法之一，但是有遗憾的是没办法标识最佳连续子序列的位置
     */
    public static int maxSubSum4(int[] a) {
        int maxSum = 0;
        int tempSum = 0;

        for (int i = 0; i < a.length; i++) {
            tempSum += a[i];

            if (tempSum > maxSum)
                maxSum = tempSum;
            else if (tempSum < 0)
                tempSum = 0;
        }
        return maxSum;
    }

5、O（N）的动态规划算法

/**
     * 求解思路：用sum(j)表示a1到aj的和，很容易求出动态规划的递归式：
     *  sum(j) = max(sum(j-1)+aj , aj)
     * 时间复杂度：O(N)
     * 动态规划的好处在于，能很清楚的返回最佳连续子序列和的起始位置和终点位置
     *
     */
    public static int maxSubSum5(int[] a) {
        int maxSum = 0;
        int tempSum = 0;
        int begin = 0;

        for (int i = 0; i < a.length; i++) {
            if (tempSum > 0)
                tempSum += a[i];
            else {
                tempSum = a[i];
                begin = i;  //标记
            }

            if (tempSum > maxSum) {
                maxSum = tempSum;
                //可以在这里获取最佳连续子序列和的起点位置begin和重点位置i
            }

        }
        return maxSum;
    }

测试

源代码

public class Main {

    public static int maxSubSum1(int[] a) {
        int maxSum = 0;
        for (int i = 0; i < a.length; i++) {
            for (int j = i; j < a.length; j++) {
                int tempSum = 0;

                for (int k = i; k <= j; k++) {
                    tempSum += a[k];
                }

                if (tempSum > maxSum) {
                    maxSum = tempSum;
                }

            }
        }
        return maxSum;
    }

    public static int maxSubSum2(int[] a) {
        int maxSum = 0;

        for (int i = 0; i < a.length; i++) {
            int tempSum = 0;

            for (int j = i; j < a.length; j++) {
                tempSum += a[j];

                if (tempSum > maxSum)
                    maxSum = tempSum;
            }
        }
        return maxSum;
    }

    public static int maxSubSum3(int[] a) {
        return subSum3(a, 0, a.length - 1);
    }

    private static int subSum3(int[] a, int left, int right) {
        if (left == right)
            if (a[left] > 0)
                return a[left];
            else
                return 0;

        int center = (left + right) / 2;
        int maxLeftSum = subSum3(a, left, center);
        int maxRightSum = subSum3(a, center + 1, right);

        int maxLeftBorderSum = 0, leftBorderSum = 0;
        for (int i = center; i >= left; i--) {
            leftBorderSum += a[i];
            if (leftBorderSum > maxLeftBorderSum)
                maxLeftBorderSum = leftBorderSum;
        }

        int maxRightBorderSum = 0, rightBorderSum = 0;
        for (int i = center + 1; i <= right; i++) {
            rightBorderSum += a[i];
            if (rightBorderSum > maxRightBorderSum)
                maxRightBorderSum = rightBorderSum;
        }

        return Math.max(Math.max(maxLeftSum, maxRightSum), maxLeftBorderSum + maxRightBorderSum);

    }

    public static int maxSubSum4(int[] a) {
        int maxSum = 0;
        int tempSum = 0;

        for (int i = 0; i < a.length; i++) {
            tempSum += a[i];

            if (tempSum > maxSum)
                maxSum = tempSum;
            else if (tempSum < 0)
                tempSum = 0;
        }
        return maxSum;
    }

    public static int maxSubSum5(int[] a) {
        int maxSum = 0;
        int tempSum = 0;
        int begin = 0;

        for (int i = 0; i < a.length; i++) {
            if (tempSum > 0)
                tempSum += a[i];
            else {
                tempSum = a[i];
                begin = i;  //标记
            }

            if (tempSum > maxSum) {
                maxSum = tempSum;
                //可以在这里获取最佳连续子序列和的起点位置begin和重点位置i
            }

        }
        return maxSum;
    }

    public static void main(String[] args) {
        // TODO Auto-generated method stub
        int[] a = { 1, -3, 7, 8, -4, 12, -10, 6 };
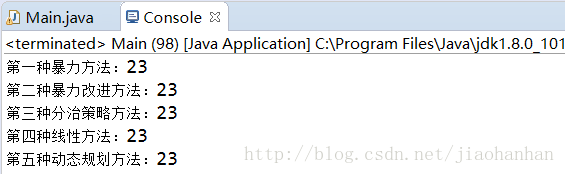
        System.out.println("第一种暴力方法：" + maxSubSum1(a));
        System.out.println("第二种暴力改进方法：" + maxSubSum2(a));
        System.out.println("第三种分治策略方法：" + maxSubSum3(a));
        System.out.println("第四种线性方法：" + maxSubSum4(a));
        System.out.println("第五种动态规划方法：" + maxSubSum5(a));
    }

}

结果：