【学习体会】图像泊松融合

图像融合后: 参考博文：从泊松方程的解法，聊到泊松图像融合 - 知乎

参考论文：Pérez P, Gangnet M, Blake A. Poisson image editing[M]//ACM SIGGRAPH 2003 Papers. 2003: 313-318.

参考代码：GitHub - cheind/poisson-image-editing: Poisson image editing for seamless cloning and other operations（注意：代码中的梯度场拉普拉斯滤波核有误）

问题分析

在图像融合任务中，前景放置在背景上时，需要保证两点：

• 前景本身主要内容相比于背景而言，尽量平滑；

• 边界处无缝，即前景、背景在边界点位置上的像素值，需要保持边界一致。

重点关注两个词：内容平滑、边界一致。

平滑是什么？可以理解成图像前景、背景梯度尽可能接近。

边界一致是指什么？可以理解成在边界上像素值相同。

用一张图来说明：

 

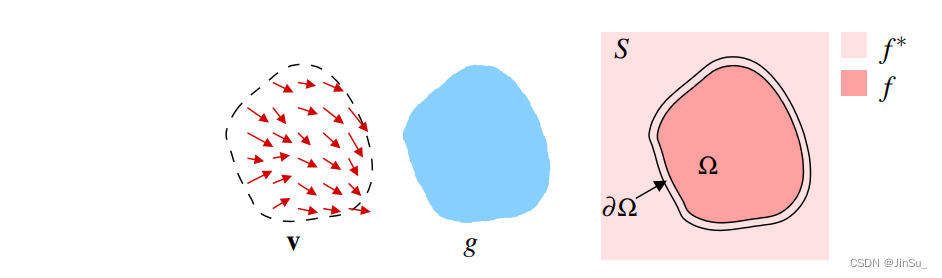
连续的泊松求解器

离散的泊松求解器

对于计算机中的图像定义域是离散的，因此我们需要将连续问题转化为离散问题：

 

 

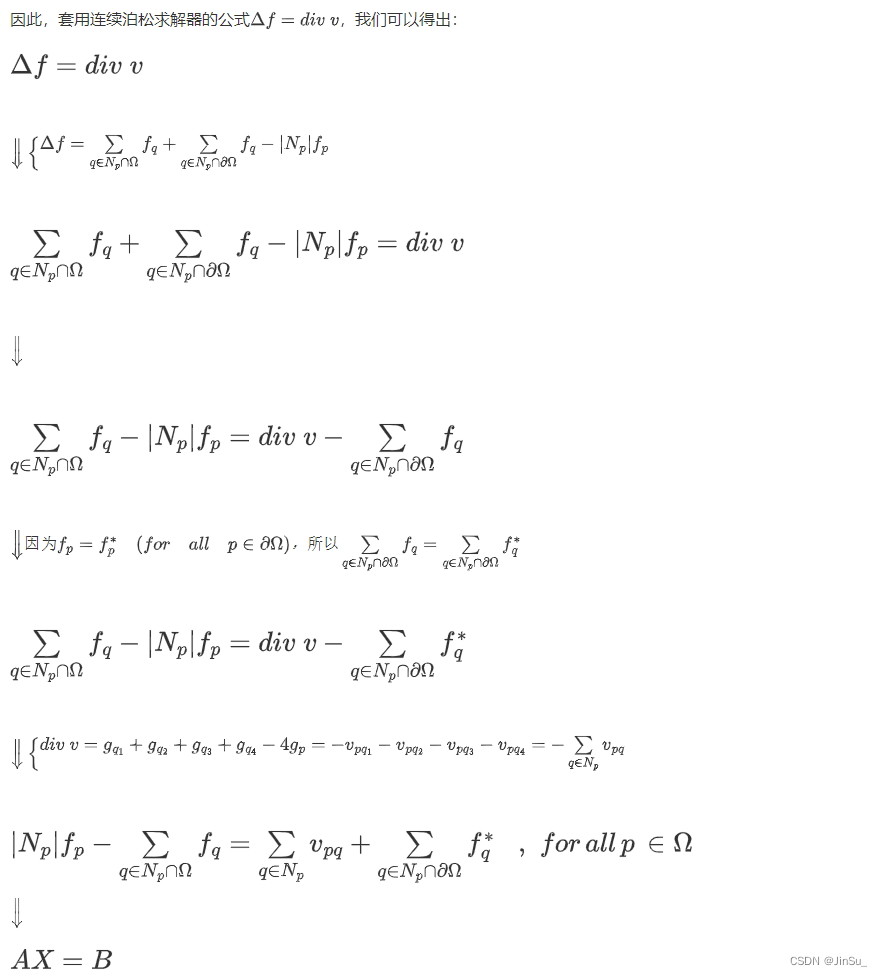
其中，重要变量的具体计算如下所示：

梯度场v的散度

 

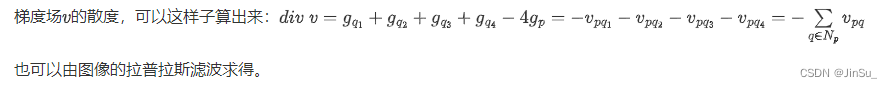
 For example, 
x方向的梯度kernelx可以是:
 `cv::Mat kernelx = (cv::Mat_<float>(1, 3) << 0 , -1, 1);`
 然后，再求拉普拉斯kernelx可以是:
 `cv::Mat kernelx = (cv::Mat_<float>(1, 3) << -1 , 1, 0);`

那么因为，
 `f = vxx + vyy`
以及根据对应的拉普拉斯kernelx
 `vxx(p.x, p.y) = vx(p.x, p.y) - vx(p.(x-1), p.y)`
以及，对应的梯度kernelx
 `vx(p.x, p.y) = g(p.(x+1), p.y)-g(p.x, p.y)  `
 `vx(p.(x-1), p.y) =g(p.x, p.y)-g(p.(x-1), p.y)`
因此，
 `vxx(p.x, p.y) = g(p.(x+1), p.y)-g(p.x, p.y)-g(p.x, p.y)+g(p.(x-1), p.y)`
 `vxx(p.x, p.y) = g(p.(x+1), p.y)+g(p.(x-1), p.y)-2*g(p.x, p.y)`
同理计算vyy，
 `vyy(p.x, p.y) = g(p.x, p.(y+1)))+g(p.y, p.(y-1))-2*g(p.x, p.y)`
因此可得梯度场的散度，
 `f =g(p.(x+1), p.y)+g(p.(x-1), p.y)+g(p.x, p.(y+1)))+g(p.y, p.(y-1))-4*g(p.x, p.y) `

参考：https://github.com/cheind/poisson-image-editing/issues/7

这里据一个错误的梯度场求散度的例子，也是参考代码中的一个疏漏：

如果，x方向的梯度kernelx和拉普拉斯kernelx都为 `cv::Mat kernelx = (cv::Mat_<float>(1, 3) << -0.5 , 0, 0.5);`

那么因为，
 `f = vxx + vyy`
以及根据对应的拉普拉斯kernelx
 `vxx(p.x, p.y) = 0.5*(-vx(p.(x-1), p.y) + vx(p.(x+1), p.y))`
以及，对应的梯度kernelx
 `vx(p.(x-1), p.y) = 0.5(-g(p.(x-2), p.y) + g(p.x, p.y))`
 `vx(p.(x+1), p.y) = 0.5(-g(p.x, p.y) + g(p.(x+2), p.y))`
因此，
 `vxx(p.x, p.y) = 0.5*( -0.5(-g(p.(x-2), p.y) + g(p.x, p.y)) + 0.5( -g(p.x, p.y) + g(p.(x+2), p.y)) )`
 `vxx(p.x, p.y) = 0.25*( g(p.(x-2), p.y) - g(p.x, p.y) - g(p.x, p.y) + g(p.(x+2), p.y) )`
 `vxx(p.x, p.y) = 0.25*(  - 2*g(p.x, p.y) + g(p.(x-2), p.y) + g(p.(x+2), p.y) )`
同理计算vyy，
 `vyy(p.x, p.y) = 0.25*(  - 2*g(p.x, p.y) + g(p.x, p.(y-2)) + g(p.x, p.(y+2)) )`
因此可得梯度场的散度，
 `f = 0.25*(  - 4*g(p.x, p.y) + g(p.x, p.(y-2)) + g(p.x, p.(y+2)) + g(p.(x-2), p.y) + g(p.(x+2), p.y)  )`

方向仍然是正确的，唯一的问题是0.25比例，而且它不完全是 p 的 4 邻居，而是 +2 和 -2 邻居。 

但由于 4-neighbor 本身只是离散梯度的近似值，因此这段代码的结果与论文非常相似，只不过还原出来的结果会略有模糊。
 

矩阵A的构建

 

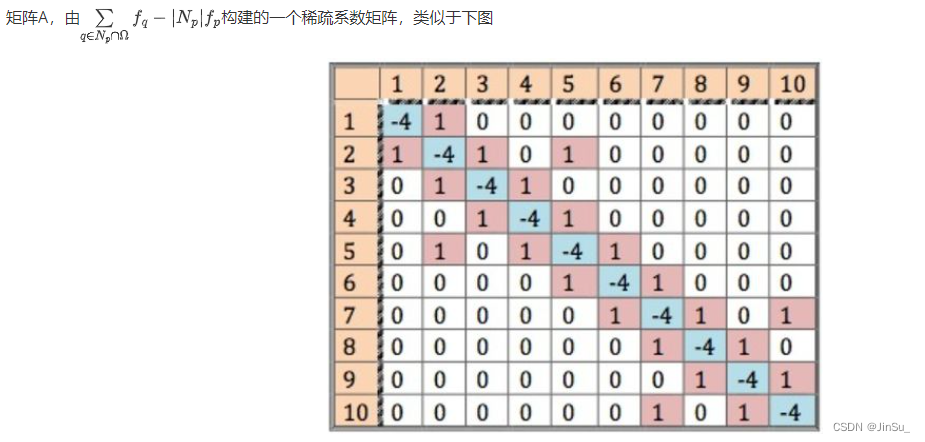
其中，这个矩阵A是正方形矩阵，即宽和高相等；每一行代表图像中mask区域的每一个像素点；

对角线的绝对值表示该点的4-neighbor的实际数量，比如-4表示该点4-neighbor的实际数量为4，比如图像边缘点的4-neighbor的实际数量可能为3或者2；非图像边缘点的默认应该都是-4；

若该点的4-neighbor中存在边界点，即mask边缘点，则在`该点对应行`中的`邻点对应列`置为0，否则置为1。

 

矩阵B的构建

代码中的一些关键参数：

// Directional indices
const int center = 0;
const int north = 1;
const int east = 2;
const int south = 3;
const int west = 4;

// Neighbor offsets in all directions
const int offsets[5][2] = { { 0, 0 }, { 0, -1 }, { 1, 0 }, { 0, 1 }, { -1, 0 } };//4-neighbor的偏移量

// Directional opposite
const int opposite[5] = { center, south, west, north, east };

float lhs[] = { -4.f, 1.f, 1.f, 1.f, 1.f };

//nUnknowns为mask区域中总的像素点数量
std::vector< Eigen::Triplet<float> > lhsTriplets;//矩阵A
lhsTriplets.reserve(nUnknowns * 5);

Eigen::MatrixXf rhs(nUnknowns, channels);//矩阵B

Eigen::SparseLU< Eigen::SparseMatrix<float> > solver;//求解器

 矩阵A和矩阵B构建过程的对应代码：

for (int n = 1; n < 5; ++n) {
    const cv::Point q(x + offsets[n][0], y + offsets[n][1]);

    const bool hasNeighbor = bounds.contains(q);
    const bool isNeighborDirichlet = hasNeighbor && (bm(q) == constants::DIRICHLET_BD);

    if (!hasNeumann && !hasNeighbor) {
        lhs[center] += lhs[n];
        lhs[n] = 0.f;
    } else if (isNeighborDirichlet) {
		rhs.row(pid) -= lhs[n] * Eigen::Map<Eigen::VectorXf>(bv.ptr<float>(q.y, q.x), channels);//rhs对应矩阵B
        lhs[n] = 0.f;
    }
}
// Add f to rhs.
rhs.row(pid) += Eigen::Map<Eigen::VectorXf>(f.ptr<float>(p.y, p.x), channels);//f对应梯度场的散度 div(v)

// Build triplets for row              
for (int n = 0; n < 5; ++n) {
    if (lhs[n] != 0.f) {
        const cv::Point q(x + offsets[n][0], y + offsets[n][1]);
        lhsTriplets.push_back(Eigen::Triplet<float>(pid, unknownIdx(q), lhs[n]));//lhsTriplets对应矩阵A
    }
}

求解AX=B

求解矩阵方程AX=B（比如，LU分解、高斯消元、最速梯度下降法、共轭梯度法等）

代码中采用Eigen::SparseMatrix构建矩阵A，因为这是个稀疏矩阵。

采用Eigen::SparseLU建立求解器solver，

将矩阵A分解为LU，即A=LU（L为下三角矩阵，U为上三角矩阵），然后就可以将问题转换为高斯消元法

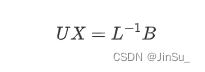
Eigen::SparseMatrix<float> A(nUnknowns, nUnknowns);
A.setFromTriplets(lhsTriplets.begin(), lhsTriplets.end());

Eigen::SparseLU< Eigen::SparseMatrix<float> > solver;
solver.analyzePattern(A);
solver.factorize(A);

Eigen::MatrixXf result(nUnknowns, channels);

for (int c = 0; c < channels; ++c)
    result.col(c) = solver.solve(rhs.col(c));

*后续可以尝试其他求解方法，包括但不限于矩阵A分块求逆、最速梯度下降法、共轭梯度法等

梯度场的定义：混合梯度

 

 

实例测试

参考代码：GitHub - cheind/poisson-image-editing: Poisson image editing for seamless cloning and other operations（注意：代码中的梯度场拉普拉斯滤波核有误）

速度会比opencv实现的版本更快一点

简单贴图

需要准备好，背景图bg，前景图fg，掩膜图mask

其中，前景图和mask图的尺寸要一致

命令行参数（参考）：

seamless_cloning ./images/bg2.bmp ./images/fg2.bmp ./images/mask2.bmp 0 0

梯度损失——图像模糊问题

对比原图和图像融合后的相同位置的梯度分布

原图：

图像融合后:

 

可以很明显地看到融合后的图像变模糊了。

原因分析：梯度场散度的离散求解精度（如果是8-neighbor会更加准确）、边界条件（Dirichlet 边界过于简单，但是也要综合考虑效率）以及泊松编辑原理本身需要考虑到边缘的过渡，模糊也是必然会发生的了。

总结

1.泊松编辑不适用于多线程，更适用于在线融合（对比多波段融合和羽化融合可以多线程处理，适用于半离线或离线处理）

2.当前的泊松编辑方法效率仍然比较慢，后续需要考虑矩阵方程AX=B的其他更高效的求解方法

3.存在编辑区域的图像模糊问题，可以尽量减少模糊至肉眼难以辨别，但是仍然存在。