作为刚上研一提前来给老师当苦力的小菜鸟,第一次学习MOEAD算法的时候,对其中介绍的分解方法一脸懵*,上网查了不少资料,很难查到详细的解释(好吧,可能我查的姿势不对),完全不理解这些分割方法所给出的表达式的意义,索性搁置了小半个月。
这里必须要感谢一下Chithon的http://blog.csdn.net/qithon/article/details/72885053#comments这篇博客,其中的两幅配图让我豁然开朗,当然,大神完全没有必要阅读这篇博客了,我只是说一下自己从向量和几何的角度是如何理解这些方法的。
Weighted Sum Approach
该方法给出的表达式为:
首先,λ被称之为权重向量,观察和式,这完全就是m维向量的点乘公式嘛。具体的说,在目标空间中,把算法求出的一个目标点和原点相连构造成一个向量,此时,该方法的做法是将该向量与对应权重向量点乘,由向量点乘的几何意义可知,所得的数为该向量在权重向量方向上的投影长度,因为权重向量不变,最大/小化该长度值其实就是在优化该向量。可知若要增大该向量在权重向量上投影的长度,一方面可以增大/减小与权重向量的夹角,另一方面可以增大/减小该向量的长度。样例图如下:








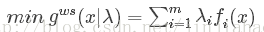
 最低0.47元/天 解锁文章
最低0.47元/天 解锁文章

















 2962
2962

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








