【题目】
请在同一个平面直角坐标系中画出一次函数y=2x, y=2x+4的图象,并观察图象,你发现这两个图形有什么位置关系?为什么?
【答案】
图象是相互平行的两条直线
【解析】
一、教学活动形式
这里设计的教学活动形式是“画图 → 观察→ 猜想 → 验证 → 证明”。
1.画图
通过描点连线,画出两个一次函数的图像。
2.观察
你俩关系太明显,一眼就能看出。
3.猜想
这俩函数有啥共同之处,对了,一次项的系数相同。那么是不是K相同的一次函数都平行呢?让孩子们的思维飞一会儿,大家伙儿一起研究研究,讨论讨论。
4.验证
再画一个试试,来个y=2x-4看看。不行就再画两个,看看是不是都有这个规律?
5.证明
之前都只是“看着”平行,你还要用演绎推理的方式证明这两个函数平行。
注意验证和证明的区别:验证是通过举例子、做实验的方法来检验结论;证明则是运用已知定理、公理,通过逻辑推理的方式,从已知条件出发推导出结论。
(1)个例证明
如图所示,函数y=2x+4与坐标轴交于A、B两点,故A点纵坐标为0、B点横坐标为0,代入函数可求得A、B的坐标分别是A(-2,0), B(0,4)。在直线y=2x上取纵坐标为4的点C,由点C向x轴画垂线,垂足为D。纵坐标为4(CD=4),代入函数,可求得横坐标为2(0D=2)。则△AOB≌△OD C(SAS)得∠BAO=∠COD,从而有AB∥CD。
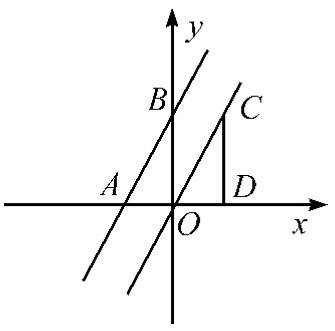
然而,这只是证明了y=2x, y=2x+4这两个函数平行,并不能由此得出结论“一次项系数k相同的一次函数相互平行”。
(2)命题证明
要再进一步引导学生证明上述命题成立,即一般形式的y=kx,y=kx+b具有平行关系。
其实证明思路和前面完全一样,只需用字母代替前面的数即可(代数法)。
同样可以求出函数y=kx+b与坐标轴交点的坐标为(-b/k, 0),(0, b),在函数y=kx上取纵坐标为b的点,该点的坐标为(b/k, b)。于是,我们同样能通过证明两个三角形相等的形式证明两直线平行。
二、总结反思
这道题的证明首先要画辅助线构造三角形,再通过证明三角形全等得出同位角相等,进而证明两直线平行。
问题来了,我们是怎么想到解题思路的呢?
一切都要从问题出发。
要证明两直线平行,只有通过角的关系证明。只有三种渠道:同位角相等、内错角相等、同旁内角互补。
你要明白,这三种方法其实只是一种。因为后两种都是由第一种推导出来的。
第一种是最直接、最直观的证明方法,应该是我们首选的证明方法。
第二种次之,第三种因为不能通过角相等证明,因此很少用。
无论哪种证明方法,都需要有“截线”(与两条平行线都相交的线,即截断两条线的线)。
画面上正有两条天然截线:X轴、Y轴。
要证明角相等,那全等三角形是不二之选。
你一眼看过去,画面上已有一个三角形,就是y=kx+b与坐标轴构成的那个三角形。

所以自然会想到以y=kx为一条边,再构造一个三角形,与这个三角形相等,于是你想到要画辅助线。
怎么画辅助线呢?看看画面上已有的那个三角形,两条直角边,一条斜边。斜边有了,所以你肯定是要画直角边了。
前面给出的证明方法是画平行于Y轴的辅助线构造三角形,能不能用平行于X轴的辅助线构造全等三角形呢?当然可以!
能不能通过内错角相等证明呢,当然也可以,无非要构造的三角形不同,要画的辅助线不同而已。
最后,总结下证明思路:证明平行←同位角相等←全等三角形←画辅助线构造三角形。



























 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










