信号的两种表现形式-时域和频域

目录

时域信号

时域和频域信号的关系

非周期信号

---

时域信号

        时域上，电信号的幅度是随着时间变化的。其图形，是示波器常用的显示模式。

        同时，也可以用矢量投影来表示随时间变化的波形。

        这两种显示模式之间的关系，如下图所示，可以通过一个简单的正弦信号显示出来。

        时间轴上的振幅对应于投影在虚轴上的矢量分量，即：

        矢量的角频率可以由下式得到：

时域和频域信号的关系

        时域和频域这两种表示形式，可以通过傅里叶变换相互关联。

        所以时域中的每一个信号都在频域中对应相应的频谱。

        傅里叶变换公式，如下图所示。

周期信号

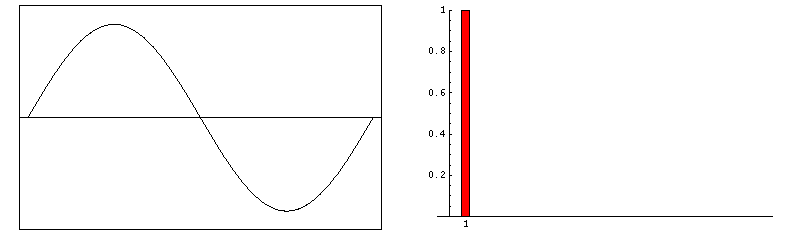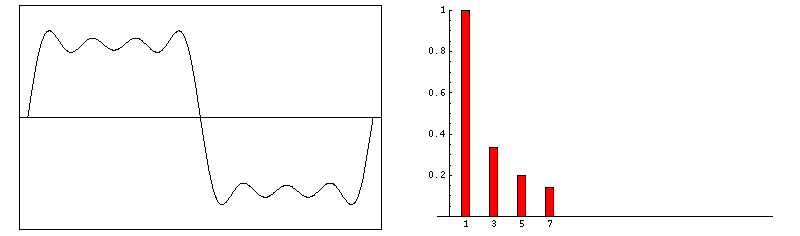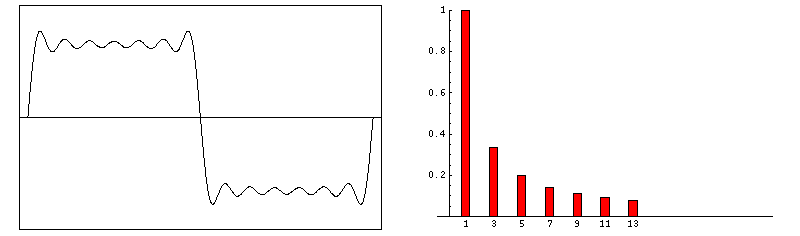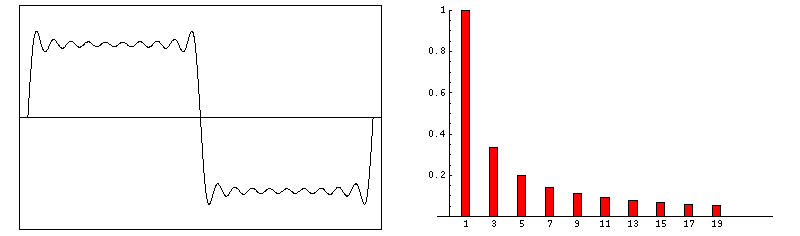
        根据傅里叶定理，任何时间域中的周期性信号都可以分解为不同频率和振幅的正弦/余弦信号的总和。这样的总和被称为傅里叶级数。如下图所示：

        下图表示了，傅里叶级数前四项之和。

        当谐波数量增多时，信号就越接近于理想的矩形脉冲。

        当信号为余弦信号时，其频谱为：

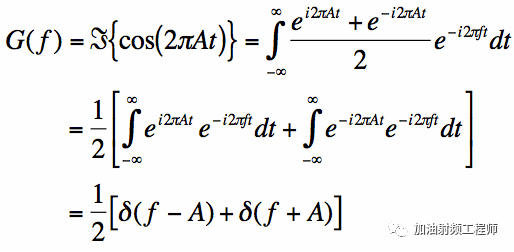
        当信号为正弦信号时，其频谱为：

        可以看出，正弦和余弦信号的频谱都由狄拉克脉冲组成，而且他们的傅里叶变换在幅度上是相同的，因此这两个信号在同一频率处表现出相同的幅度谱。

        一个周期性信号的频谱，可以用傅里叶级数来表示。级数中的每一个分量，在频域都对应一个迪拉克脉冲，它是频域中的一个离散分量。因此，周期性信号总是表现出离散频谱，也被称为线谱。

        下图是近似矩形信号对应的时域分量和频域分量。

下图是一些周期信号在时域和频域的表示。

非周期信号

        那周期信号可以用傅里叶级数来表示，但是非周期信号呢？

        非周期信号的频谱可以通过傅里叶变换来计算，其频谱不是由离散频谱分量组成的。非周期信号在频域为连续频谱，其频谱密度与频率有关。

        与正弦和余弦信号类似，对于许多信号来说，都能获得确切的表达式。

        但对于在时域具有随机特性的信号，如噪声或随机比特序列，则很少能得到相应的频域解。在这种情况下，频谱可以则一般通过数值解来确定。

        下图中是一些非周期信号在时域和频域的表示。

        当要看时域波形时，可以用示波器进行测量；当要看频域波形时，可以用频谱仪进行测量。

        下图所示的信号似乎是一个频率为20MHz的纯正弦波信号。同样，大家也期望在频域，只有20MHz的单根频谱。

        但是，借助频谱分析仪在频域中检查该信号时，发现除了基波之外，还有几个高阶谐波。所以，谐波分量则在时域中看不出来。

参考文献：

Christoph Rauscher， Fundamentals of Spectrum Analysis

下载链接：

链接：https://pan.baidu.com/s/1sf0Kw1KLvxnftmRpHsHstg

提取码：y38i