一、实验目的
- 了解聚类的概念和层次聚类的方法
- 实现三种不同的层次聚类算法
- 对比三种不同算法在不同的数据集的情况下的性能
二、代码框架
-
本次实验使用的函数框架如下:
1.create_sample(mean, cov, num, label) #生成样本均值向量为mean,协方差矩阵为cov的,数量为num,标签为label的数据集 2.PoMinkowski(x1,x2,dimension,p=2) #两样本点之间Minkowski距离,dimension表示样本的特征维数,p=2时,计算的是欧氏距离 3.clusingle(clu1,clu2,dimension,p=2) #最短距离/单连接 (single linkage) 4.clucomplete(clu1,clu2,dimension,p=2) #最⻓距离/全连接 (complete linkage) 5.cluaverage(clu1,clu2,dimension,p=2) #平均距离 (average linkage) 6.discluster(cluster,dimension,kind=0,p=2) #类距离矩阵的生成,kind表示使用3,4,5中的哪种方法生成类距离矩阵 7.dismin(distance) #根据类距离矩阵确定距离最近的两个类 8.update(cluster,res) #更新类,将cluster中的res编号的两个类合并 9.datastat(cluster) #数据统计,统计合并完成后生成的三个类的数据 10.aggregation(cluster,dimension,kind=0,p=2) #聚合操作 11.makeplt3D(List) #根据List绘制三维点空间分布图 12.makeplt2D(List,label1) #根据List和label绘制分布直方图
三、代码详解
-
产生数据
# 生成数据 def create_sample(mean, cov, num, label): ''' :param mean: 均值向量 :param cov: 协方差矩阵 :param num: 数量 :param label: 标签 :return: 最终生成的数据前三列表示特征,后一列表示便签 ''' x,y,z=np.random.multivariate_normal(mean,cov,num).T L = np.ones(num)*label X=np.array([x,y,z,L]) return X.T使用
np.random.multivariate_normal函数生成均值向量为mean,协方差矩阵为cov,数量为num,标签为label的样本数据。 -
两点之间的距离计算
def PoMinkowski(x1,x2,dimension,p=2): ''' :param x1: 点x1 :param x2: 点x2 :param dimension: 两个点所在的空间维度 :param p: 参数p=2时为欧氏距离 :return: 距离 ''' dis = 0 for i in range(dimension): dis = dis + math.pow(x1[i]-x2[i],p) return math.sqrt(dis)
在本次试验中使用闵可夫斯基距离进行计算,默认使用p=2,即计算两个点之间的欧氏距离 -
三种层次聚类算法(基本要求和中级要求)
# 最短距离single linkage def clusingle(clu1,clu2,dimension,p=2): Min = float("inf") for i in range(len(clu1)): for j in range(len(clu2)): d=PoMinkowski(clu1[i],clu2[j],dimension,p) Min = d if d < Min else Min return Min # 最长距离complete linkage def clucomplete(clu1,clu2,dimension,p=2): Max = float("-inf") for i in range(len(clu1)): for j in range(len(clu2)): d = PoMinkowski(clu1[i],clu2[j],dimension,p) Max = d if d>Max else Max return Max # 平均距离average linkage def cluaverage(clu1,clu2,dimension,p=2): d = 0 for i in range(len(clu1)): for j in range(len(clu2)): d = d + PoMinkowski(clu1[i],clu2[j],dimension,p) ans = d/(len(clu1)*len(clu2)) return ans
使用三种不同的方法(如上图)计算两个类之间的距离,类中两个点之间的距离还是使用欧式距离
-
生成类距离矩阵
# 类距离矩阵生成 def discluster(cluster,dimension,kind=0,p=2): ''' :param cluster: 类组成的集合 :param dimension: 点的维度 :param p: p=2 表示欧式距离 :param kind: 使用哪种方法求类距离 :return: 类距离矩阵 ''' if kind == 0: func = clusingle elif kind == 1: func = clucomplete elif kind == 2: func = cluaverage else: print("para:'kind' error") exit(0) templist = np.zeros((len(cluster),len(cluster))) for i in range(len(cluster)): for j in range(len(cluster)): templist[i][j]=func(cluster[i],cluster[j],dimension,p) return templistkind表示使用哪一种层次聚类方法,定义func为函数指针,templist[i][j]表示第i个类和第j个类的距离
-
找到距离最近的两个类的下标,便于后面的合并
# 找到类集合中距离最近的两个类 def dismin(distance): ''' :param distance: 类距离矩阵 :return: 距离最近的两个类的坐标 ''' Min = float("inf") res=[0,0] for i in range(len(distance)): for j in range(len(distance)): if i!=j and distance[i][j] < Min: Min = distance[i][j] res = [i,j] return res当i=j时表示的是类和自身的距离,始终为零,当i=j时不需要合并,所以排除j=i的情况,当迭代过类距离矩阵之后,res中储存的是距离最小的两个类的编号
-
合并两个类
# 聚合操作,更新类 def update(cluster,res): a = cluster[res[0]] b = cluster[res[1]] a.extend(b) cluster.remove(b)使用extend将b合并到a中,使用remove从cluster中移除b,实现a和b的合并
-
数据统计
# 数据统计 def datastat(cluster): ''' :param cluster: 合并之后的类 :return: count 统计结果 label三类的标签 ''' # count统计合并聚类后的三个类中分别含有三种类别样本集合的数量 count = [[0,0,0],[0,0,0],[0,0,0]] for i in range(3): for j in range(len(cluster[i])): count[i][int(cluster[i][j][3]-1)]+=1 count=np.array(count) # 数量最多的类作为合并后这一类的类标签 label = count.argmax(axis=1)+1 return count,label统计合并之后每一类中不同类标签的数量储存在count中,count[0][2]表示cluster[0]中类标签为3的样本数量,列表label中储存合并后每一类是什么标签(根据这一类中最多的类标签),label[0]储存着cluster[0]是哪一类
-
聚合聚类
# 聚合聚类 def aggregation(cluster,dimension,kind=0,p=2): ''' :param cluster: 样本空间 :param dimension: 维度 :param kind: 求类距离的方法 :param p: 欧氏距离 :return: 聚合后的样本空间 ''' i = 0 # 当类的个数多与3时合并继续 while(len(cluster)>3): # 每一次迭代都重新产生类距离矩阵 distance = discluster(cluster, dimension, kind, p) # 求出距离最近的两个类的下标 res = dismin(distance) # 合并两个类 update(cluster,res) -
绘图函数
# 绘制三维空间分布图 def makeplt3D(List): point = np.array(List) fig = plt.figure() ax = fig.add_subplot(111,projection='3d') print(point) n=len(point) #print(n) clu = [] for i in range(3): clu.append(list(point[point[:,3]==i+1])) #print(clu) # symbol中储存点的形状和颜色等 symbol = [['r','o'],['b','^'],['g','p']] for i in range(3): temp=[list(c) for c in clu[i]] temp=np.array(temp) x = temp[:,0] y = temp[:,1] z = temp[:,2] ax.scatter(x,y,z,c=symbol[i][0],marker=symbol[i][1]) ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') plt.show() # 绘制分布直方图 def makeplt2D(List,label1): plt.bar([0.6, 1.7, 2.7], List[0], width=0.2, label=str(label1[0])) plt.bar([1, 2, 3], List[1], width=0.2, label=str(label1[1])) plt.bar([1.3, 2.3, 3.3], List[2], width=0.2, label=str(label1[2])) plt.legend() plt.xlabel('预测类别') plt.ylabel('数量') plt.title(u'预测类别-数量条形图') plt.show() -
主体函数
if __name__ == "__main__": # 参数设置 mean = np.array([[1,1,1],[2,2,2],[3,3,3]]) cov = [[0.7,0,0],[0,0.7,0],[0,0,0.7]] n = 501 P = 1/3 num = [round(n*P) for i in range(3)] total = 0 # clus储存合并后的矩阵 clus1 = [] # 数据生成并集合 for i in range(3): total += num[i] clus1.extend(create_sample(mean[i],cov,num[i],i+1)) # 将矩阵转为类 clus=[[list(c)] for c in clus1] print("总共产生了{}个样本".format(total)) for i in range(3): cor = 0 # 深拷贝 cluster = copy.deepcopy(clus) # 打乱顺序(没什么用) random.shuffle(cluster) # 聚合聚类 aggregation(cluster,3,i) # string中储存了三个字符串 print("使用{}-linkage层次聚类算法".format(string[i])) # 返回统计信息 count, label = datastat(cluster) # 输出每一种层次聚类方法的统计信息 for i in range(3): print("cluster[{}]标签为{}".format(i,label[i])) print("每一类的构成及错误率如下:") print("cluster\t类\t类1\t类2\t类3\t错误率\n") for i in range(3): print(" ",i,"\t",label[i],end="") for j in range(3): print("\t{}".format(count[i][j],j+1),end="") cor += count[i][label[i]-1] print("\t{}\n".format(1-count[i][label[i]-1]/sum(count[i])),end="") print("综上:总的错误率为{}".format(1-cor/total))在这里,要注意的点是
-
在生成数据的时候,我们要将每一个数据转换为二维列表:因为
在第一次产生类距离矩阵的时候,我们计算两个类之间的距离,在这个过程中需要计算两个类中每个点之间的距离,如果类是一个一维列表,如下

此时每个列表中的样本数据为一个array数组,可以认为是一维数组。然后运行,结果报错如下:
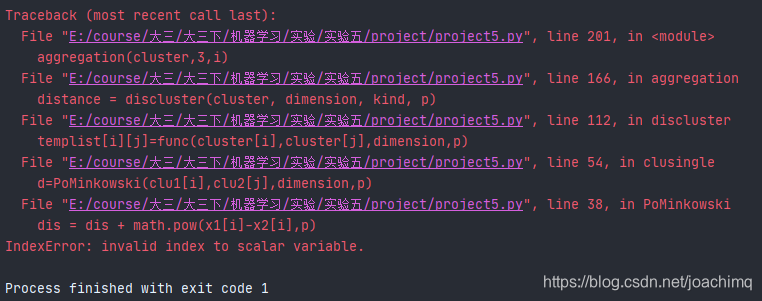
显示无效的下标,这是因为在层次聚类函数中,我们需要对每个类中的每个点进行计算,遍历过程如下:
Min = float("inf") for i in range(len(clu1)): for j in range(len(clu2)): d=PoMinkowski(clu1[i],clu2[j],dimension,p) Min = d if d < Min else Min return Min两重循环遍历两个类中的所有点,但是在第一次遍历的过程中,每个类只有一个点,此时我们每个类是一维向量,range(len(clu1))却是等于4(三个特征值,一个标签),所以在计算点距离的时候x1和x2不是点而是float型的特征值,所以会报错。
-
除此之外,我们在生成数据的时候数据不能为array类型,只能为基本的list类型否则会报错如下:

这是因为在使用list.remove(arg)的过程中,程序首先在list中匹配和arg相等的元素,相等为true,不等为false,涉及到了数据的比较运算。但是,array类型元素的比较不太一样,它返回的是一组的bool值示例如下:
a = np.array([1,2,3]) b = np.array([1,2,4]) print(type(a),type(b)) print(a == b)
比较两个array类型的数据,可以使用any和all,如下:print(any(a==b)) print(all(a==b))
综上两点使用如下方法转换数据为我们需要的数据:clus=[[list(c)] for c in clus1]
-
四、实验结果
(在这里使用不同的协方差矩阵进行对比分析)
(1) 实现 single-linkage 层次聚类算法
(2) 实现complete-linkage 层次聚类算法
(3) 实现average-linkage层次聚类算法
在这里使用生成102个样本(2000个样本运行有些慢)
当协方差矩阵为[[5, 0, 0], [0, 5, 0], [0, 0, 5]]时:

当协方差为5时,三种类别的层次聚类算法的错误率都很高,都到了50%以上,而且我们发现此时的样本聚类都是聚集在某一类中,PS:我们的数据集中三类数据是平均产生的,相比较而言,此时的average-linkage层次聚类算法的性能比较好。
当协方差矩阵为[[0.5, 0, 0], [0, 0.5, 0], [0, 0, 0.5]]时:
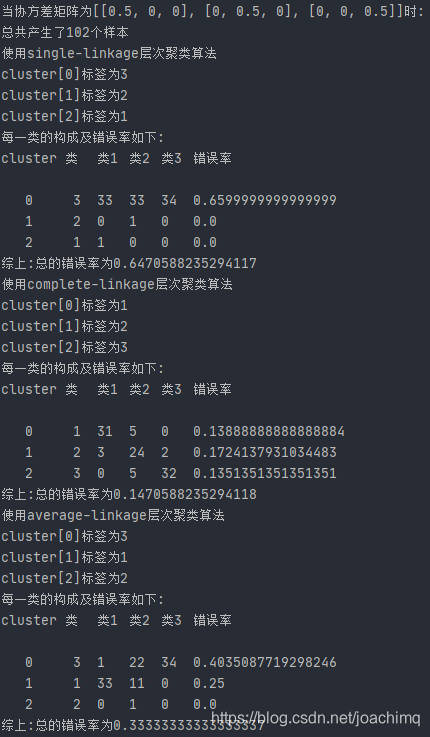
当协方差为0.5时,single和average算法仍然出现了严重的分类不均问题。single-linkage算法的错误率并没有明显的下降,仍然为65%上下,complete-linkage算法下降为了14.7%,average-link算法的错误率下降为了33%,此时性能最好的仍然是complete-link层次聚类算法
当协方差矩阵为[[0.05, 0, 0], [0, 0.05, 0], [0, 0, 0.05]]时

当协方差为0.05时,三者的分类准确率均为100%,没有可比性,因为当协方差为0.05时,三类数据都是泾渭分明的,如下图:
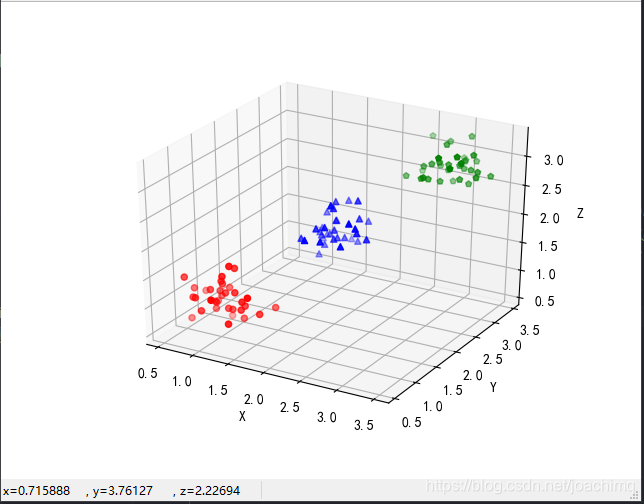
(4) 绘图聚类前后样本分布情况
聚类前后样本点在空间中的位置并没有改变(以协方差为0.5为例),如下图:

聚类后三类的分布直方图(以协方差=0.5为例)如下:
此时的数据如下



























 3078
3078

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










