问题描述

解析
思路:轻者先装,直到再装任何集装箱将使轮船载重量超过B时停止。
定理:对于任何正整数n,算法(轻者先装)对n个集装箱的实例得到最优解。
证明(数学归纳法):
(1)k=1,只有1个集装箱,其重量小于B。任何装法都只有一种方式,因此都是最优解。故轻者先装也是最优解。
(2)归纳假设:假设算法对于规模为n的输入都能得到最优解。
考虑规模为n+1的输入,
N
=
{
1
,
2
,
.
.
.
,
n
+
1
}
,
W
=
{
w
1
,
w
2
,
.
.
.
,
w
n
+
1
}
N=\left\{1,2,...,n+1\right\},W=\left\{w_1,w_2,...,w_{n+1}\right\}
N={1,2,...,n+1},W={w1,w2,...,wn+1}
是集装箱的重量。其中,
w
1
≤
w
2
≤
.
.
.
≤
w
n
+
1
w_1\leq w_2\leq...\leq w_{n+1}
w1≤w2≤...≤wn+1
现在从N中取出最轻的集装箱,得到n规模的输入:
N
′
=
N
−
{
1
}
=
{
2
,
3
,
.
.
.
,
n
+
1
}
N'=N-\left\{ 1\right\}=\left\{ 2,3,...,n+1\right\}
N′=N−{1}={2,3,...,n+1}
W
′
=
W
−
{
w
1
}
W'=W-\left\{ w_1\right\}
W′=W−{w1}
B
′
=
B
−
w
1
B'=B-w_1
B′=B−w1
根据归纳假设,对于n个输入,N’,W’,B’的最优解为I’,即I’为N’,不含1的最优解,令
I
=
I
′
I=I'
I=I′
⋃
\bigcup
⋃
{
1
}
\left\{ 1\right\}
{1}
那么I必然是N的最优解,这也是算法对于N,W,C的解。
证明(反证法):I必然是N的最优解。
(1)构建最优解
I
∗
I^*
I∗(N,含1):假设I不是N的最优解。则必然存在最优解
I
∗
I^*
I∗,如果
I
I
I中没有1,用
I
I
I替代
I
I
I中的第一个集装箱标号得到的解也是最优解(这是因为个数不变,故也是最优解),使得I为包含1的关于N的最优解,且
∣
I
∗
∣
>
∣
I
∣
| I ^*| > | I|
∣I∗∣>∣I∣。
(2)构建最优解
I
∗
’
I^*’
I∗’(N’,不含1):因为I包含1的关于N的最优解,构建的
I
’
=
I
∗
−
{
1
}
I’= I^* - \left\{ 1\right\}
I’=I∗−{1} 是不包含1的最优解,即关于N’、W’、C’的最优解(N’、W’、C’不包含1)。
注:此处利用反证法证明
I
∗
’
=
I
∗
−
{
1
}
I^*’= I^* - \left\{ 1\right\}
I∗’=I∗−{1} 是不包含1的最优解。
证明:若
I
∗
‘
=
I
∗
−
{
1
}
I^*‘= I^* - \left\{ 1\right\}
I∗‘=I∗−{1}不是不包含1的最优解,则存在最优解
I
∗
’
’
I^*’’
I∗’’(
N
’
N’
N’,不含1),使得
∣
I
∗
’
∣
<
∣
I
∗
’
’
∣
|I^* ’| < | I^*’’|
∣I∗’∣<∣I∗’’∣,
即
∣
I
∗
’
+
{
1
}
∣
<
∣
I
∗
’
’
+
{
1
}
∣
|I^* ’+ \left\{ 1\right\} | < | I^*’’+ \left\{ 1\right\}|
∣I∗’+{1}∣<∣I∗’’+{1}∣,与
I
∗
’
+
{
1
}
=
I
I^*’+ \left\{ 1\right\} = I
I∗’+{1}=I为最优解相矛盾,因此
I
’
=
I
∗
−
{
1
}
I’= I^* - \left\{ 1\right\}
I’=I∗−{1}是不包含1 的最优解。
(3)构建的最优解I*’与归纳假设的最优解I’比较:
由(1)
∣
I
∗
∣
>
∣
I
∣
| I^* | > | I |
∣I∗∣>∣I∣得,
∣
I
∗
’
∣
=
∣
I
∗
−
{
1
}
∣
>
∣
I
−
{
1
}
∣
=
∣
I
’
∣
|I^*’|=|I^*-\left\{ 1\right\}|>|I - \left\{ 1\right\}|=|I’|
∣I∗’∣=∣I∗−{1}∣>∣I−{1}∣=∣I’∣,与
I
’
I’
I’的最优性矛盾。
综上所述,假设命题不成立,原命题成立,即I必然是N的最优解。
装载问题(0-1背包问题)举例
w1 = 2,w2 = 2,w3 = 6,w4 = 5,w5 = 4
v1 = 6,v2 = 3,v3 = 5,v4 = 4,v5 = 6
B = 10
V(i,j)表

V(5,10) = 15 > V(4,10) = 14 => x5 = 1 且 j = j - w5 = 10 - 4 = 6;
V(4,6) = 9 = V(3,6) = 9 => x4 = 0;
V(3,6) = 9 = V(2,6) = 9 => x3 = 0;
V(2,6) = 9 > V(1,6) = 6 => x2 = 1 且 j = j - w2 = 6 - 2 = 4;
V(1,4) = 6 > V(0,4) = 0 => x1 = 1 且 j = j - w1 = 4 - 2 = 2;
故放入背包的物品为物品1,物品2和物品5。
算法伪代码
For i= 1…n
For j = 1…B
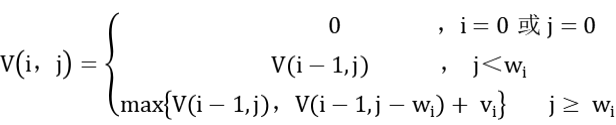




















 3148
3148











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








