股票/期货/期权历史波动率测算方法汇总

---

文章仅分享了波动率测算代码实例，尚未完成波动率对比

一、close to close

公式：
$$\hat{\sigma }=\sqrt{\frac{{\sum }_{i=1}^N(r_i-\mu {)}^2}{N}}$$

二、Parkinson 1980. aka High low HV

公式：
$${\hat{\sigma }}_{parkinson\_N}=\sqrt{\frac{1}{4Nln2}\sum _{i=1}^{N}ln(\frac{H_i}{L_i}{)}^2}$$
$H_i$为最高价，$L_i$为最低价。

Python代码如下：

def calculate_parkinson_volatility(data, col_high, col_low, period, trading_periods=252,ori=1):
    #计算parkinson_volatility
    #参数为：data数据列；col_high：最高价列列名；col_low：最低价列列名；n：计算周期；ori：数据日期方向，1降序，-1升序，默认降序。
    rs = (1.0 /(4.0*np.log(2)))*((data[col_high] / data[col_low]).apply(np.log))** 2 #求和项内数据
    
    def f(v):
        return (trading_periods * v.mean())**0.5
    
    #计算parkinson_volatility
    if ori == 1:
        volatility = rs.rolling(window=period,center=False).apply(func=f).shift(-period+1)
        
    elif ori == -1:
        volatility = rs.rolling(window=period,center=False).apply(func=f)
    else:
        print("请检查数据为升序/降序")
        
    return volatility

三、Garman&Klass 波动率

公式：
$${\sigma }_N=\sqrt{\frac{1}{2N}[\sum _{i=1}^{N}ln(\frac{H_i}{L_i}{)}^2-2(2ln2-1)\sum _{i=1}^{N}ln(\frac{C_i}{O_i}{)}^2]}$$
$H_i$为最高价，$L_i$为最低价，$C_i$为最高价，$O_i$为最低价。

Python代码如下：

def calculate_garman_klass_volatility(data, col_high, col_low, col_close,col_open, period,trading_periods=252,ori=1):
    # 计算garman_klass_volatility
    # 参数为：data数据列；col_high：最高价列列名；col_low：最低价列列名；col_close;收盘价列名称；col_open:开盘价列名
    # n：计算周期；ori：数据日期方向，1降序，-1升序，默认降序。
    log_hl = np.log(data[col_high] / data[col_low])  # 最高价和最低价的对数差平方
    log_co = np.log(data[col_close]/ data[col_open]) # 收盘价的对数差平方

    rs = 0.5 * log_hl**2 - (2*np.log(2)-1) * log_co**2
    
    def f(v):
        return (trading_periods * v.mean())**0.5

    # 计算Garman-Klass波动率
    if ori == 1:
        volatility = rs.rolling(window=period).apply(f).shift(-period+1)
    elif ori == -1:
        volatility = rs.rolling(window=period)
    else:
        print("请检查数据为升序/降序")
    return volatility

四、 Rogers & Satchell 波动率

公式：
$${\sigma }_N=\sqrt{\frac{1}{N}\sum _{i=1}^N[ln(\frac{H_i}{L_i})ln(\frac{H_i}{O_i})+ln(\frac{L_i}{C_i})ln(\frac{L_i}{O_i})]}$$
$H_i$为最高价，$L_i$为最低价，$C_i$为最高价，$O_i$为最低价。

Python代码如下：

def calculate_rogers_satchell_volatility(data, col_high, col_low, col_close, col_open, period, trading_periods=252,ori=1):
    # 计算rogers_satchell_volatility
    # 参数为：data数据列；col_high：最高价列列名；col_low：最低价列列名；col_close;收盘价列名称；col_open:开盘价列名
    # n：计算周期；ori：数据日期方向，1降序，-1升序，默认降序。
    log_hc = np.log(data[col_high]/data[col_close]) # high/close
    log_ho = np.log(data[col_high]/data[col_open])  # high/open
    log_lc = np.log(data[col_low]/data[col_close]) # low/close
    log_lo = np.log(data[col_low]/data[col_open])  # low/open
    
    rs = log_hc*log_ho +log_lc*log_lo
    
    def f(v):
        return (trading_periods * v.mean())**0.5
    
    if ori == 1:
        volatility = rs.rolling(window=period,center=False).apply(func=f).shift(-period+1)
    elif ori == -1:
        volatility = rs.rolling(window=period,center=False).apply(func=f)
    else:
        print("请检查数据为升序/降序")
    return volatility

五、小结

• 需要注意的是：上述公式仅计算了日波动率，一般报告年波动率，所以需要使用交易日期，进行相应调整，即：乘上trading periods（252）的平方根。
• 关于各种波动率的对比，可参考文章：[【Option 101】【未完成】历史波动率的不同度量方法]。(https://blog.csdn.net/AdamNi_NintyNine/article/details/122808220)
  本人也才刚开始学习，暂时不知哪种方法测算波动率更实用，后续学习填坑。
• github上也有现成的包：volatility-trading，可以直接用现成的代码包。为了方便后续使用，本次项目仅参考其中核心计算部分代码并进行一定修改，有对比过测算结果，结果一致。

六、测算实例

以螺纹钢为例，分别使用三种方法测算螺纹钢的波动率，并画图：

import pandas as pd
import numpy as np
data = pd.read_excel("黑色能化量价数据.xlsx",index_col=0)

def calculate_parkinson_volatility(data, col_high, col_low, period, trading_periods=252,ori=1):
    #计算parkinson_volatility
    #参数为：data数据列；col_high：最高价列列名；col_low：最低价列列名；n：计算周期；ori：数据日期方向，1降序，-1升序，默认降序。
    rs = (1.0 /(4.0*np.log(2)))*((data[col_high] / data[col_low]).apply(np.log))** 2 #求和项内数据
    
    def f(v):
        return (trading_periods * v.mean())**0.5
    
    #计算parkinson_volatility
    if ori == 1:
        volatility = rs.rolling(window=period,center=False).apply(func=f).shift(-period+1)
        
    elif ori == -1:
        volatility = rs.rolling(window=period,center=False).apply(func=f)
    else:
        print("请检查数据为升序/降序")
        
    return volatility

col_close = data.columns[3]
col_high = data.columns[2]
col_low = data.columns[1]
col_open = data.columns[0]

period_list = [5,20,120]
name ="螺纹钢"
for period in period_list:
    col_volatility_name = name + ":"+str(period)+"日parkinson波动率"
    data[col_volatility_name] = calculate_parkinson_volatility(data, col_high, col_low, period, ori=1)

通过上述代码计算得到Parkinson波动率，画图如下：

parkinson波动率

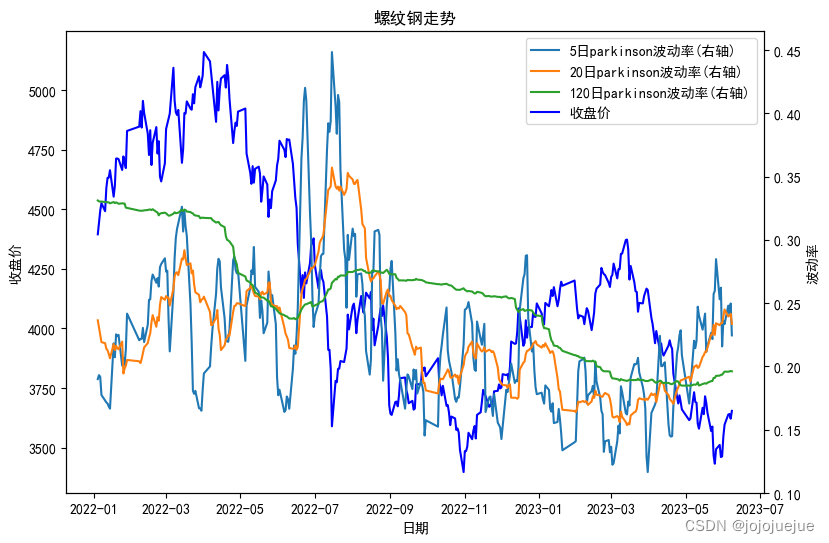
类似的可以得到：

garmen&klass波动率

rogers&satchell波动率

最后汇总对比三种波动率

三种波动率汇总

完整实例见代码包附件