本章内容和第四章的不定积分其实大差不差,然而不定积分本身与求和无关,本质为求导的逆运算;而定积分则和求导无关,实质为无限分割再求和。而牛顿莱布尼茨公式的伟大之处在于,可以用不定积分这个求导的逆运算来计算定积分的值,定积分与不定积分有很大的联系。
定积分是积分的一种,是函数f(x)在区间[a,b]上积分和的极限。
这里应注意定积分与不定积分之间的关系:若定积分存在,则它是一个具体的数值,而不定积分是一个函数表达式,它们仅仅在数学上有一个计算关系(牛顿-莱布尼茨公式)。
一个函数,可以存在不定积分,而不存在定积分;也可以存在定积分,而不存在不定积分。一个连续函数,一定存在定积分和不定积分;若只有有限个间断点,则定积分存在;若有跳跃间断点,则原函数一定不存在,即不定积分一定不存在。
一般定理
定理1:设f(x)在区间[a,b]上连续,则f(x)在[a,b]上可积。
定理2:设f(x)区间[a,b]上有界,且只有有限个间断点,则f(x)在[a,b]上可积。
定理3:设f(x)在区间[a,b]上单调,则f(x)在[a,b]上可积。
牛顿-莱布尼茨公式
定积分与不定积分看起来风马牛不相及,但是由于一个数学上重要的理论的支撑,使得它们有了本质的密切关系。把一个图形无限细分再累加,这似乎是不可能的事情,但是由于这个理论,可以转化为计算积分。
目录
考研数学一大纲中对这一章的要求如下:
1.理解积分上限的函数,会求它的导数,掌握牛顿-莱布尼茨公式.
2.理解反常积分的概念,了解反常积分收敛的比较判别法,会计算反常积分.
3.掌握用定积分表达和计算一些几何量与物理量(平面图形的面积、平面曲线的弧长、旋转体的体积及侧面积、平行截面面积为已知的立体体积、功、引力、压力、质心、形心等)及函数的平均值.
5.1定积分的概念与性质
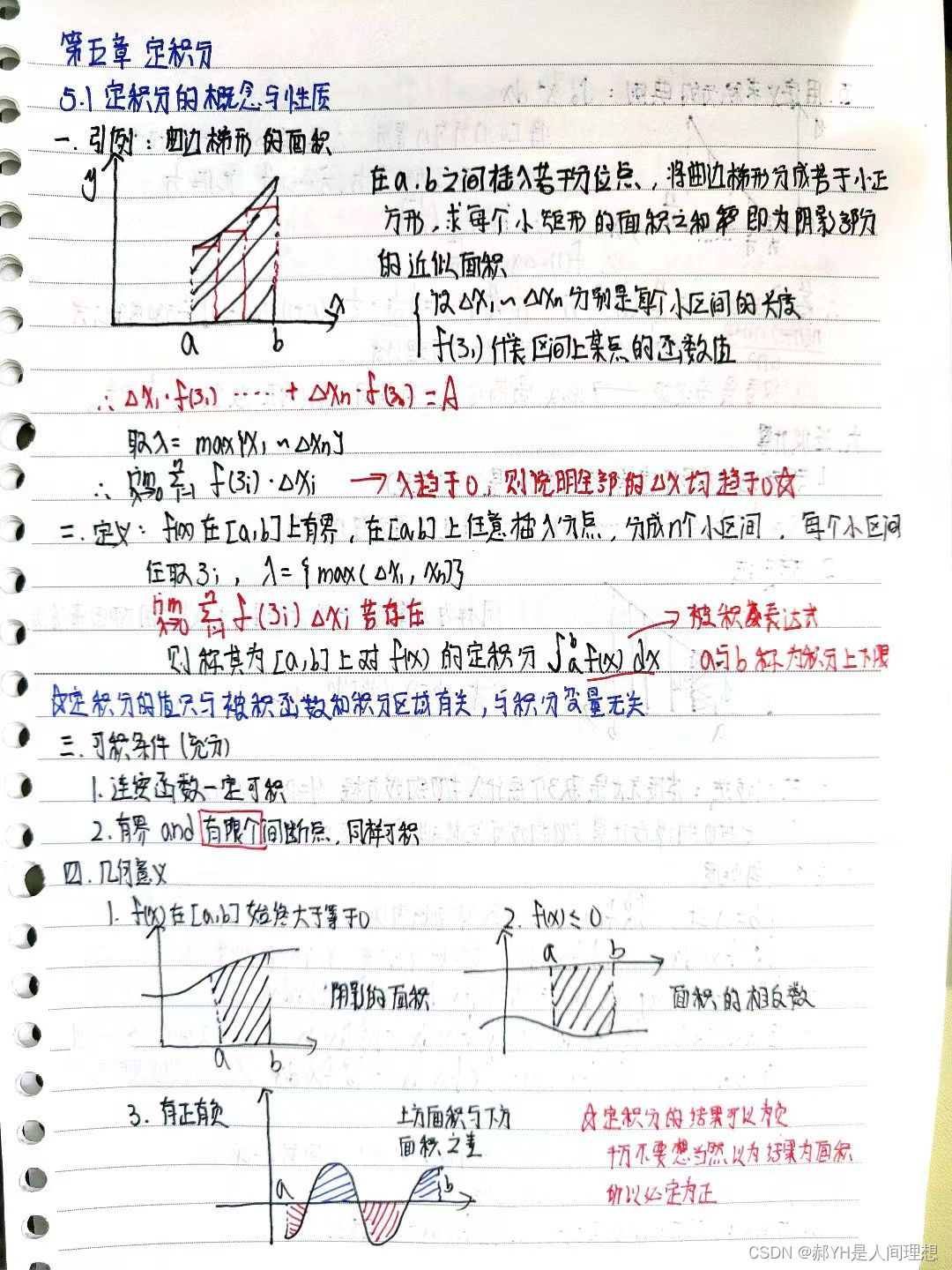
- 由不规则面积的计算引出
- 在a、b之间插入若干个分位点,将曲边梯形分成若干个小正方形,求每个小矩形的面积之和即为阴影部分的近似面积~
- 定积分的值只和被积分函数和积分区域有关,与积分变量无关
- 连续函数一定可积,or有界and有限个间断点,同样可积~
- 交换积分上下限,积分的前面要加负号~
- 定积分中值定理:如果f(x)为连续函数,存在【a,b】上的点x0,有f(x0)*(b-a)=a到b之上对x的积分~
- 定积分也有自己的介值定理,其他内容看笔记~
5.2微积分基本公式
- 积分上限函数:积出关于积分上限的函数,结果与积分变量是谁无关(本质上就是将未知的上限x代入到“原函数”之中,改变的不过是变量名~)
- 如果f(x)连续,则积分上限函数可导
- 不定积分的意义是原函数的全体
- 牛顿莱布尼茨公式的意义在于,直接将定积分求面积的过程转换为了求原函数的过程
5.3定积分的换元法and分部积分法
- 定积分在换元的时候,要注意上下限也要换
- 分部积分和不定积分中的套路基本上一致,仔细看一下就好
5.4反常积分
分为无穷限的广义积分和无界函数的广义积分~
5.5无穷限的反常积分
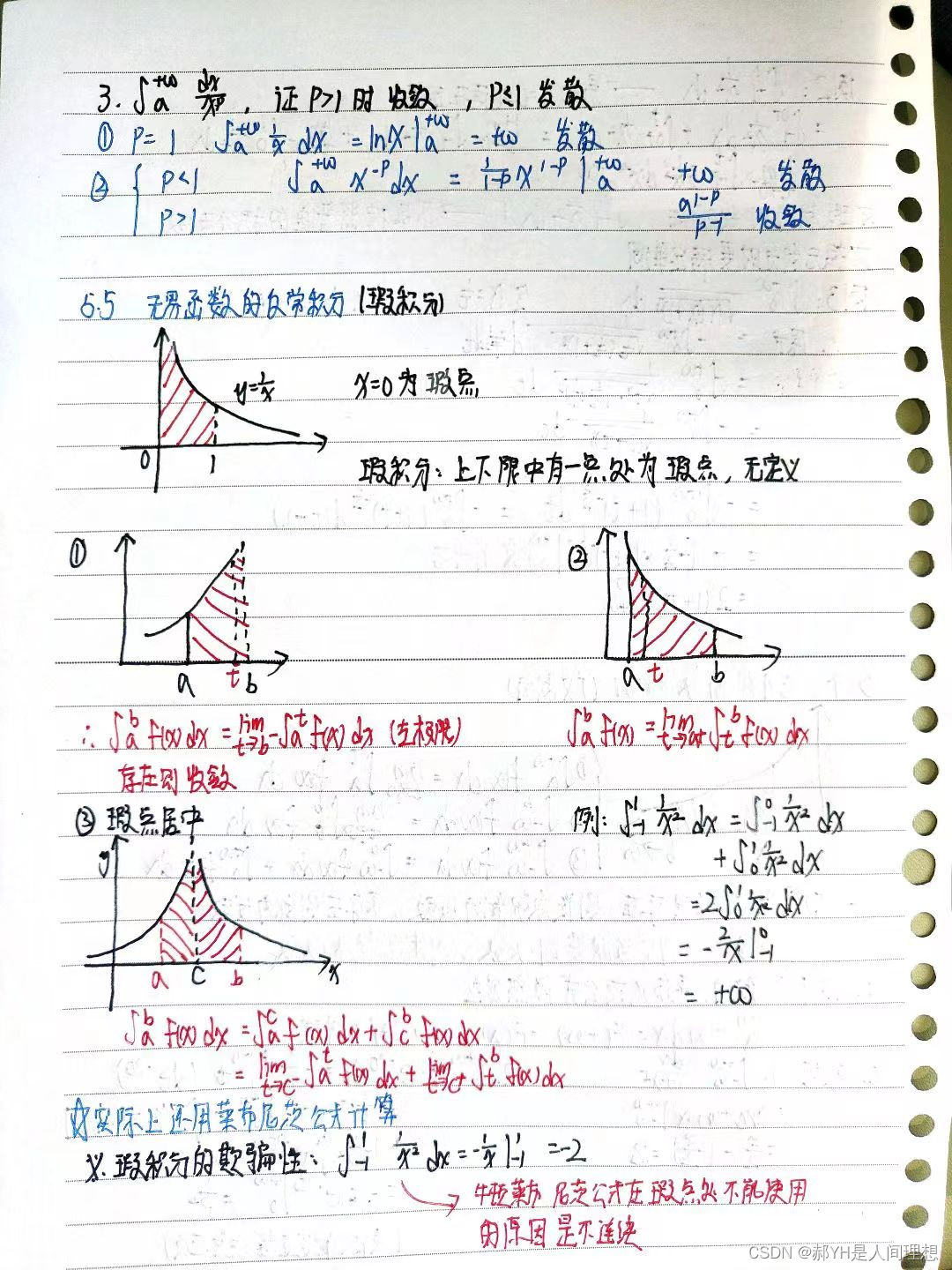
- 指的是上下限有一个是趋于无穷的情况~
5.6无界函数的反常积分
- 瑕积分:上下限有一点处为瑕点,无定义~































 9236
9236

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










