编译原理之FIRST集FOLLOW集

从老师的PPT上整理下来，加了一些自己的理解（//解释的部分）。

//可以只看‘FIRST集的求法’和‘FOLLOW集的计算’。

 

FIRST集的定义 ：

设G=(V_T,V_N,P,S)是上下文无关文法

FIRST(a)={a|a=>*ab,a∈V_T, a,b∈V^*}

若a=>*ε则规定ε∈FIRST (a)

FIRST(α)就是从α可能推导出的所有开头终结符号和可能的ε所构成的集合。

FIRST集的分析方法 ：

对于文法中的符号X∈VN∪VT，其FIRST(X)集合可反复应用下列规则计算，直到其FIRST(X)集合不再增大为止：

1)若 X∈VT，则FIRST(X)={X}。

2)若X∈VN，且具有形如X→aα的产生式(a∈VT)，或具有形如X→ε的产生式，则把a或ε加进FIRST(X)。//把X能推出的第一个终结符加入FIRST（X）。

3) 设G中有形如X→Y₁…Y_k的产生式,其中X,Y₁…Y_k∈V_N，且Y₁…Y_i-1均能=>*ε(1≤i≤k)，则FIRST(Y₁)-{ε},…, FIRST(Y_i-1)-{ε},FIRST(Y_i)都包含在FIRST(X)中。// Y_i推导不出ε，所以Y_i+1不在FIRST（X）中。

4) 若对一切1≤i≤k，均有ε∈FIRST(Y_i)，则将ε符号加进FIRST(X)。//若X=>*ε,则将ε加入FIRST（X）。

 

FIRST集的求法：

对于文法G的任一符号串α=X₁X₂…X_n可按下列步骤构造其FIRST(α)集合：

1) 置FIRST(α)=φ

2) 将FIRST(X₁)中的一切非ε符号加进FIRST(α)；

3) 若ε∈FIRST(X₁)，将FIRST(X₂)中的一切非ε符号加进FIRST(α)；若ε∈FIRST(X₁)和FIRST(X₂)，将FIRST(X₃)中的一切非ε符号加进FIRST(α)；依次类推。//根据分析方法中的第3条，若该符号能推出ε则将下一个符号的FIRST集加入FIRST(α)，以此类推。

4)若对于一切1≤i≤n,ε∈FIRST(X_i)，则将ε符号加进FIRST(α)。 //根据分析方法的第4条，若右侧符号串的每个符号都能推出ε，则α肯定能推出ε，所以将ε加进FIRST（α）。

 

例：

   E  →TE’

   E’→+TE’

   E’→ε

   T  →FT’

   T’→*FT’

   T’→ε

   F→(E)|i

FIRST(E)=FIRST(T)=FIRST(F)={ ( ，i } //FIRST（T）不包含ε，所以FIRST（E）不包含FIRST（E’），根据求法的第3条，T无法推出ε为向右类推的终止条件。同理：FIRST（T）不包含FIRST（T’）。

FIRST(E’)= { + ，ε}

FIRST(T’)={ * ，ε}

//遇到E  →TE’这样的产生式，先把FISRT（T）放入FIRST（E），再看看T能否推导出ε，若能推出，则把FIRST(E’)放入FIRST（E），以此类推。

若T不能推出ε，则FIRST（E）求完了。若遇到终结符，请看分析方法第一条。

 

关系图法求文法符号的FIRST集

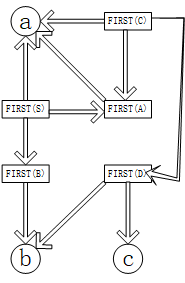
(1) 每个文法符号对应图中一个结点，终结符用其本身作标记，非终结符A用FIRST(A)标记。

(2) 如果文法中有产生式Α→αXβ,且α=>*ε  ，则从A对应的结点到X对应的结点连一条弧。

(3) 凡是从FIRST(A)结点有路径可达的终结符均为FIRST(A)的成员。

(4) 确定ε是否为非终结符FIRST集的成员，若是则加入。

 例：

     S→AB

     S→bC

     A→ε

     A→b

     B→ε

     B→aD

     C→AD

     C→b

     D→aS

     D→c

由图可知：

FIRST(S)={a,b,ε}

FIRST(A)={b,ε}

FIRST(B)={a,ε}

FIRST(C)={a,b,c}

FIRST(D)={a,c}

FOLLOW集定义

FOLLOW(A)={a| S=>*mAb 且a∈FIRST(b),m∈V*,b∈V+}

若 S=>*uAb, 且b =>*ε,则#∈FOLLOW( A)。

 

FOLLOW集的计算

1. 对于文法的开始符号S，置#于FOLLOW(S) 中;

2. 若Ａ→αBβ是一个产生式,则把FIRST(β)-{e}加至FOLLOW(B)中;若β=>*e (即eÎFIRST(β))，则把FOLLOW(A)加至FOLLOW(B)中。//若B有可能是最后一个符号，则把

FOLLOW(A)加至FOLLOW(B)中，否则把FIRST(β)- {e}加至FOLLOW(B)中。

反复使用上述规则，直到所求FOLLOW集不再增大为止。

注意: 在FOLLOW集合中无ε。

//FIRST集从产生式左侧推导，而FOLLOW集从产生式右侧推导。例如求A的FIRST集，要先从产生式左侧找到A，然后根据产生式右侧的信息求出A的FIRST集；求A的FOLLOW集时，要先从产生式右侧找到A，然后根据A右侧的符号信息求出A的FOLLOW集。

 

例：

E→TE’，

E’→+TE’，

E’→ε，

  T→FT’，

T’→*FT’，

T’→ε，

F→(E)|i

FOLLOW(E)= {)，#}，//E为开始符号，加入#，E的后面有终结符)

FOLLOW(E’)= FOLLOW(E)={ ) ，# } //第一个产生式中E’是最后一个符号，所以FOLLOW(E’）中加入FOLLOW(E)。

FOLLOW(T)={FIRST(E’)-{e}}∪FOLLOW(E)∪FOLLOW(E’) = { + ， ) ， # } //第一个产生是中T后面有非终结符E’，所以在FOLLOW(T)中加入{FIRST(E’)-{e}}，而E’→ε，所以T有可能是最后一个符号，所以把FOLLOW(E)加入FOLLOW(T)；同理第二个产生式中，要把FOLLOW(E’)加入FOLLOW(T)。

FOLLOW(T’)= FOLLOW(T)= { + ， ) ， # }

FOLLOW(F)={FIRST(T’)-{e}})∪FOLLOW(T)∪FOLLOW(T’) = {+，*，) ，# }  

关系图法计算FOLLOW集:

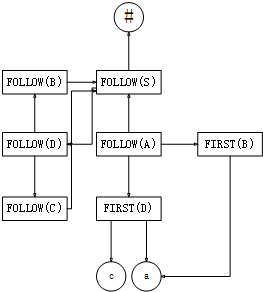
1.文法G中的每个符号和‘#’对应图中的一个结点，对应终结符和‘#’的结点用符号本身标记。对应非终结符的结点用FOLLOW(A)或FIRST(A)标记。

2.从开始符号S的FOLLOW(S)结点到‘#’号的结点连一条箭弧。

3.如果文法中有产生式A→αBβX，且β=>*ε，则从FOLLOW(B)结点到FIRST(X)结点连一条弧，当X∈VT时，则与X相联。

4.如果文法中有产生式A→αBβ，且β=>*ε，则从FOLLOW(B)结点到FOLLOW(X)结点连一条弧。

5.对每一FIRST(A)结点如果有产生式A→αXβ，且α=>*ε，则从FIRST(A)到FIRST(X)连一条弧。

例：

S→AB

S→bC

A→ε

A→b

B→ε

B→aD

C→AD

C→b

D→aS

D→c

由图可知：

FOLLOW(S)={#}

FOLLOW(A)={a,#,c}

FOLLOW(B)={#}

FOLLOW(C)={#}

FOLLOW(D)={#}