自动驾驶卡车局部路径优化

港口场景中自动驾驶卡车的局部路径优化器

摘要

最近，诸如CHOMP之类的函数梯度算法在为铰接式机器人生成局部最优运动规划方面取得了巨大成功。本文将CHOMP改进并应用于非完整车辆，例如带单拖车的自动驾驶卡车和差速驱动机器人。在这两种系统上实现了带有滚动约束的扩展CHOMP，获得了可行曲率。本文详细介绍了扩展CHOMP运动规划器与沃尔沃FH‐16自动驾驶卡车的传感器融合及控制系统进行实验集成的过程，并说明了在差速驱动机器人上开展的实验。在真实环境中的初步实验研究和结果表明，CHOMP能够为移动机器人和车辆生成平滑且无碰撞轨迹。最后，本文讨论了将CHOMP应用于移动机器人的可行性。

1 引言

本工作的动机来自Cargo‐ANTs欧盟项目1该项目旨在创建能够在共享工作空间中协同作业的智能自动导引车（AGV）和自动驾驶卡车（ATs），以实现高效、安全的货物运输。在主要港口和货运码头[13]。整个项目的背景提出了在集装箱码头等受限室外环境中针对自动导引车和自动驾驶卡车的多机器人/车辆路径规划的研究问题。尽管存在集中式和分布式等不同的多机器人/车辆路径规划方法，但已提出一种名为SPADES的专用导航框架[5]。

SPADES（动态环境中同时规划与分配）框架（图1）基于类似于[8]的多机器人任务分配方法。该框架由运行在港口中央站的全局任务分配和全局路径规划器，以及运行在各自动驾驶卡车上的本地互联路径适配器组成。全局任务分配模块基于经典匈牙利算法[6]对每辆车辆分配任务，以最小化所有车辆的总路径长度。因此，在静态环境中，每个车辆都会从其所有可能的任务中获得一个最优任务（例如，A车辆取N个集装箱，B车辆取O个集装箱等）。最小化标准是每辆车的路径长度，该长度由全局路径规划器模块提供。该模块计算车辆‐集装箱‐目标组合之间的所有可能路径。每个组合的成本采用简单的导航函数，从而使整体任务分配和路径规划更高效。生成的轨迹随后由局部路径适配器持续优化，以避免与动态障碍物发生碰撞或与其他路径产生冲突。当遇到动态障碍物时，由于局部路径适配器对路径进行优化，原本为所有车辆分配的最优路径可能会失去最优性。然而，系统始终能产生近似最优解。这是因为冲突通过考虑其他车辆的轨迹在本地得到解决。

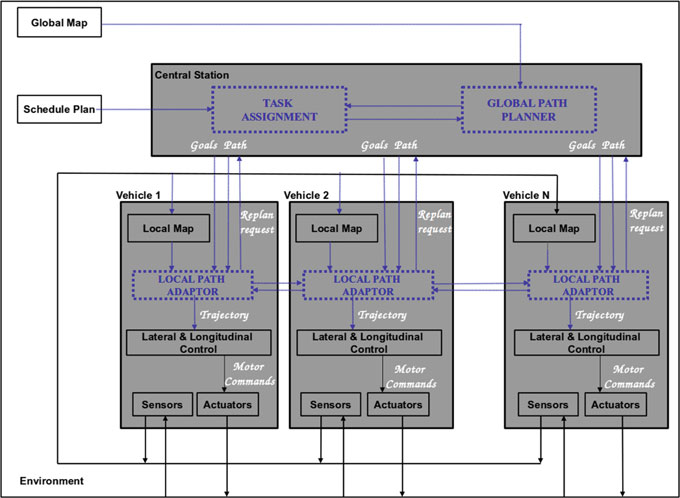
本文详细阐述了SPADES框架中较低层的导航框架，重点介绍了针对非完整车辆的局部路径适配器的改进方法、其在沃尔沃FH‐16卡车上的实现细节以及开展的实际实验。我们还通过与turtlebot2差速驱动机器人进行对比，分析该方法的有效程度。下一节将介绍与多机器人路径规划中使用的局部避障技术相关的近期研究工作。第3节详细说明了局部路径适配器及其在移动机器人上的适配方法。实现细节在第5节中进行解释，随后介绍了车辆软件架构。结果与讨论在最后的第6和7节中阐述，并在第8节给出结论。

2 相关工作

在多机器人运动规划领域，尤其是针对智能车辆的研究已有大量文献[7]。对于局部路径调整，许多简单的避障技术[12]都可以被采用。其中，互惠速度障碍（RVO）方法[15]是一种著名的反应式技术，适用于多车场景。该方法是对早期速度障碍概念的扩展。此外，RVO还有一些近期的泛化方法，能够处理显著的运动学和动力学约束[1]。需要注意的是，这类反应式避障技术更适合在每辆车辆上进行车载执行，因为它能够在不可预见的情况下提高安全性。然而，在资源瓶颈处这种策略可能会失效，例如当所有交通流必须通过一个单一闸口时。这也由于非最优解而降低了系统的吞吐量。

基于梯度的路径优化方法在铰接式机器人中取得了很大成功。它们速度快，且能生成局部最优解。对于SPADES框架而言，需要一种非常快速的反应式方法与任务分配相结合。这是因为在出现非常紧张的局部路径冲突情况时，需要从中央站的全局路径规划器进行重新规划。因此，本文旨在采用[9]的CHOMP算法作为SPADES的局部路径自适应算法。该算法用于根据局部障碍物对全局路径规划器生成的路径进行优化，在本例中即E∗算法[11]为一组自动驾驶车辆生成的路径。本文通过在优化器中引入简单的约束条件，将CHOMP算法扩展应用于移动机器人/车辆。在第3节中，详细阐述了CHOMP算法的概念及其扩展。

3 CHOMP 基础知识

CHOMP代表用于运动规划的协变哈密顿优化，由[9]提出。它是一种用于高维空间中运动规划的轨迹优化技术，能够生成不违反动力学约束的近似最优解。CHOMP通过优化一个权衡平滑度和避障等期望特性的目标泛函，迭代地改进初始轨迹的质量。CHOMP的另一个优点是其对所采用的轨迹参数化方式具有固有的不变性。给定一条轨迹ξ：[0, 1] → C，即从时间到机器人位形的映射函数，CHOMP优化一个泛函U：ξ → R，该泛函将轨迹空间ξ中的每条轨迹ξ映射为一个实数。在CHOMP的原始公式中，优化的目标泛函如下所示：
$$
U[\xi]= F_{obs}[\xi]+ \lambda F_{smooth}[\xi], \tag{1}
$$
其中，$F_{smooth}$项根据速度和加速度等动力学标准对轨迹进行惩罚，以鼓励生成平滑的轨迹。同时，$F_{obs}$项对靠近环境中物体的情况进行惩罚，以鼓励轨迹避开障碍物。为了在SPADES架构中为AGV车队集成CHOMP，必须对其进行调整以包含机器人/车辆的非完整约束。在本节中，我们详细阐述了将这些约束纳入CHOMP的方法，以便将其用于此类机器人/车辆。

主要目标是将曲率约束纳入类似CHOMP的轨迹优化器中。然而，问题在于初始猜测轨迹的吸引域内可能不存在可行的曲率约束轨迹，特别是在我们的系统中，当前的初始猜测包含显著的简化。我们看到两种选择：要么确保初始猜测轨迹始终良好，要么采用能够切换吸引域的优化器。这种隐含的系统级权衡超出了本文的范围，属于正在进行的研究内容。

为了解决这个问题，尝试了多种在不改变CHOMP本质的前提下进行的方法，这些方法在[2]中进行了详细阐述。本文推导了一种如[9]所述的约束CHOMP方法，从而为非完整车辆生成可行的轨迹。在Cargo‐ANTs项目中，我们假设用于初始化CHOMP的全局规划路径足够接近一条满足曲率约束的轨迹，并且通过一个软性曲率最大化目标函数足以使优化器不违反曲率约束。在实际应用中，该方法在经过测试的低杂乱场景中表现良好。

4 非完整约束

CHOMP算法通过改变更新规则，利用拉格朗日乘子在其原始形式中引入额外的约束。类似地，我们在此通过拉格朗日乘子法在优化步骤中显式地将运动学约束添加到CHOMP中。为了避免该过程影响实时性能，我们选择仅通过此方法包含滚动和前进运动约束。为此，我们将其表述为等式约束，如下所示。通过这样做，平滑度得到提高，直至满足曲率约束。

因此，我们首先分别表述滚动约束和前进运动约束。滚动约束表示后轴中点必须沿垂直于后轮轴线的方向移动，即
$$
x’ \sin(\theta) - y’ \cos(\theta)= 0, \tag{2}
$$
其中$x’$和$y’$是自动驾驶卡车沿x轴和y轴的全局线速度，$\theta$是车辆朝向。因此，对于由$n+ 1$个离散车辆位形$q_i=(x_i,y_i, \theta_i)$组成的轨迹，我们的滚动约束泛函可表示如下
$$
H_{roll}(\xi)=
\sum_{t=0}^{n-1} \frac{x_{t+1} -x_t}{\Delta t} \sin(\theta_t) - \frac{y_{t+1} - y_t}{\Delta t} \cos(\theta_t). \tag{3}
$$

接下来，为了确保向前运动，我们可以约束自动驾驶卡车在车辆本地坐标系中的前进速度始终为正，即
$$
\left| x’ R \right| = x’_R, \tag{4}
$$
其中$x’_R$是车辆本地坐标系R中沿x轴的速度。因此，对于包含$n+ 1$个离散车辆位形的轨迹，我们的前进运动约束泛函可表示如下，
$$
H {fwd}(\xi)= \frac{1}{\Delta t} \sum_{t=0}^{n-1} (x_{t+1} -x_t) \cos(\theta_t)+(y_{t+1} - y_t) \sin(\theta_t) - \left| (x_{t+1} -x_t) \cos(\theta_t)+(y_{t+1} - y_t) \sin(\theta_t) \right|. \tag{5}
$$

最后，我们的约束条件被总结为以下约束泛函
$$
H(\xi)= H_{roll}(\xi)+ H_{fwd}(\xi)= 0. \tag{6}
$$

现在，通过将该等式约束表示为约束泛函$H(\xi)= 0$，将其添加到CHOMP中。这要求按以下方式迭代更新轨迹：
$$
\xi_{i+1}= \xi_i - \frac{1}{\eta_i} A^{-1}\nabla U[\xi_i] + \frac{1}{\eta_i} A^{-1}C^\top(CA^{-1}C^\top)^{-1} \left( CA^{-1}\nabla U[\xi_i] -A^{-1}C^\top(CA^{-1}C^\top)^{-1} b \right), \tag{7}
$$
其中$A= K K^\top$，其中$K$是一个有限差分矩阵（见[9]中的公式13），$C= \partial \partial\xi H(\xi_i)$是约束泛函在$\xi_i$处的雅可比矩阵，$b=H(\xi_i)$。因此，遵循我们运动限制的轨迹更新在此通过约束泛函$H$及其雅可比矩阵$C$和$b$来表述。

5 实时集成

约束CHOMP已与自动驾驶卡车的传感器融合和控制系统集成。需要注意的是，整体SPADES框架在中央站中由单一的全局路径规划器与全局场地规划器共同计算最优路径。然而，在本文中，我们仅研究局部路径适配器（即约束CHOMP）在单个车辆上的性能，而非整个SPADES框架。因此，在该车辆上运行了类似E∗的全局路径规划器，以为约束CHOMP生成路径。此外，CHOMP中考虑其他车辆轨迹以调整自身路径的干扰目标也被排除在外。本节将详细说明约束CHOMP在不包含干扰目标的情况下，与局部地图、全局路径规划器及车辆控制系统的集成。

5.1 自动驾驶卡车和传感器

一辆带牵引车的沃尔沃FH‐16卡车4 × 2被用于Cargo‐ANTs项目，如图6所示。图2中说明了安装在卡车上的传感器。传感器包括GPS、前摄像头、两个带有7层的IBEO lux激光扫描仪、一个前雷达以及在卡车和挂车两侧各安装的四个德尔福短程雷达。系统配备了一个导航PC，用于将高层级传感器信息与低层级处理的感知信息进行融合，以实现车辆定位、跟踪功能，并结合地图存储与分发功能进行协同工作。

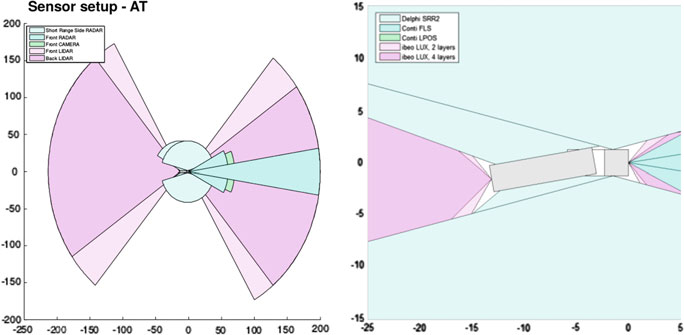
它配备Intel Core i3 1.6Ghz处理器，运行Ubuntu 14.04和ROS Indigo版本。通过在受限区域内驾驶自动驾驶卡车生成离线的全局网格地图，并在此地图中对自动驾驶卡车进行定位[3]。导航PC用于运行全局建图包，并存储该全局地图，如图3所示。

在卡车自动驾驶过程中，该导航PC在存储的全局地图上运行全局路径规划器并确定其位置。E∗算法会生成从起点到目标点的平滑插值航点。该路径由n个(x,y)离散航点组成，这些航点被分割成车辆前方20米长度的较小路径段。导航PC还运行一个动态

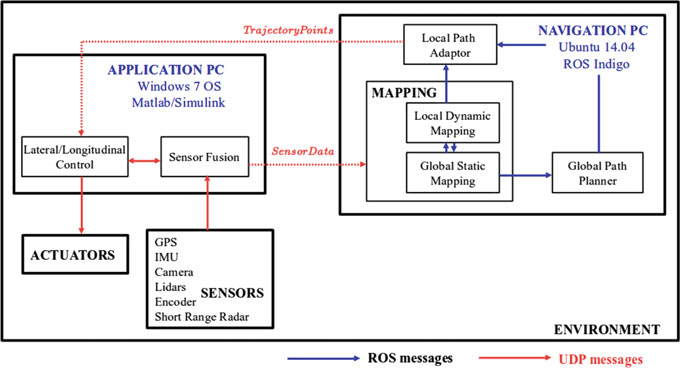
局部地图同时生成表示动态障碍物的折线图。在本例中，局部路径适配器即约束CHOMP，每20秒接收一次输入，输入包括长度为20米的剪枝路径（起点为当前位置，目标点位于卡车前方20米处）以及局部地图。因此，随着起点和终点每1米移动一次，约束CHOMP会不断生成新的轨迹。随后，它生成路径的期望轨迹点(x, y,th)、期望速度和加速度，分别表示为(x′, y′,th′)和(x′′, y′′,th′′)。

5.2 与控制器的集成

Cargo‐ANTs的框图如图3所示，该图详细说明了导航PC与运行在应用PC上的卡车控制之间的控制流。在图3中，卡车或应用程序的车辆控制和传感器融合组件运行在应用PC上。导航应用程序或ROS接口则运行在导航PC上。需要注意的是，导航PC运行Ubuntu 14.04，而车辆底层控制器则运行在搭载Windows 7操作系统和Matlab的应用PC上。这种架构的设计是为了便于项目中各个合作方进行独立且高效的软件开发。两台PC之间的控制通信通过UDP控制协议实现。来自卡车的传感器数据由UDP打包为ROS消息，供导航PC使用；而由约束CHOMP生成的轨迹点则被转换回UDP消息，供车辆底层控制器使用。

基于[14]方法的路径跟踪控制器用于执行期望轨迹。它接收通过UDP消息获取的轨迹航路点，并跟踪该轨迹，从而控制卡车的横向运动。输出轨迹中的期望速度和加速度用于控制卡车的纵向运动。局部路径适配器负责处理局部地图上的动态障碍物并进行避让。然而，当出现复杂场景时，局部路径适配器会向全局路径规划器请求新的路径。自动驾驶卡车还配备有紧急安全模块，当障碍物与卡车之间的距离小于0.5米时，该模块将接管卡车。

5.3 在Turtlebot机器人中的集成

通过为局部规划器开发插件，将约束CHOMP与ROS导航栈集成。现有的局部规划器（如TrajectoryRollout和动态窗口）被约束CHOMP所取代。因此，它利用base controller在move base ROS包中的功能来控制Turtlebot[4]。

6 实验

6.1 仿真 - 自动驾驶卡车

在Gazebo仿真环境中，使用ROS对模拟卡车进行了约束CHOMP的测试。港口实体的模型是利用Google SketchUp中的dae草图创建的xacro模型。该卡车模型根据实际项目中使用的沃尔沃FH‐16卡车模型的传感器布置和卡车底盘尺寸进行设计。

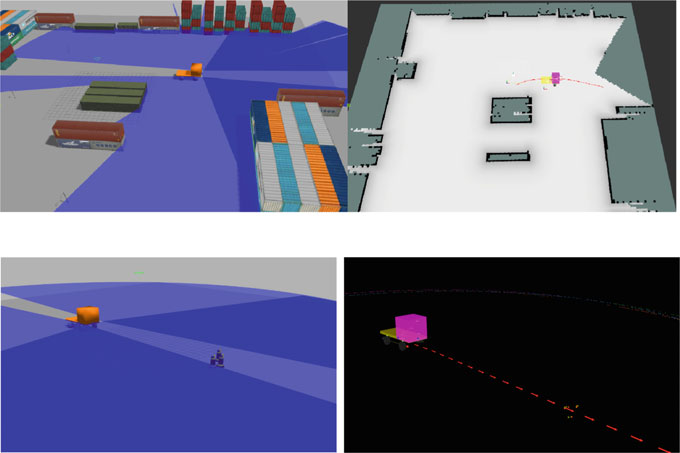
图4a是其中一个截图，展示了在Gazebo和RVIZ中模拟港口场景下自动驾驶卡车沿路径行驶的情况。图4b和c展示了另一个简单避障场景中的约束CHOMP轨迹。初始路径设定为从卡车位置出发、长度为50米的直线，该直线穿过一个意外障碍物。此初始猜测由CHOMP进行迭代，以生成适用于卡车的可行、平滑且满足约束的轨迹。两个场景采用的参数为：$\lambda= 10.00$，1毫秒时间步长，$\eta= 100$，$\xi= 20$中的位姿数量，迭代次数限制为100次。障碍物（在此情况下为三个桶）的尺寸在其原始大小基础上膨胀0.04米。

6.2 仿真 - Turtlebot

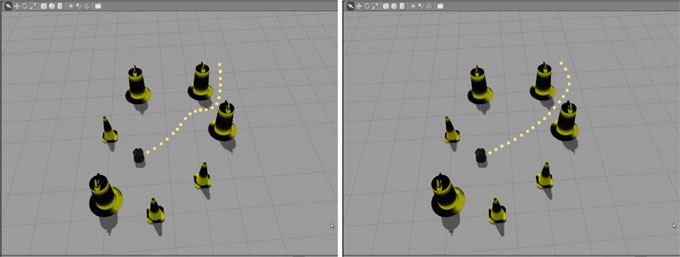
在ROS-Gazebo环境下的差速驱动机器人（Turtlebot）上测试了约束CHOMP，并使用可视化可视化器进行显示。仿真的截图如图5所示。同时比较了CHOMP生成的轨迹与约束CHOMP生成的平滑且曲率受限的轨迹。

6.3 自主卡车实车实验

在哥德堡Storaholm测试赛道上，对自动驾驶卡车单独行驶以及连接单挂车的情况分别进行了实地实验。在测试赛道中，约1.5平方公里的区域内添加了多个尺寸为 $1\times 0.75\times 1.2$米的木质托盘作为障碍物。通过两个不同的场景展示了约束CHOMP在有无障碍物情况下应用于非完整车辆的可行性。如图6所示，约束CHOMP通过生成平滑且无碰撞轨迹，成功使带挂车的卡车避开了前方障碍物。

7 讨论

7.1 性能比较

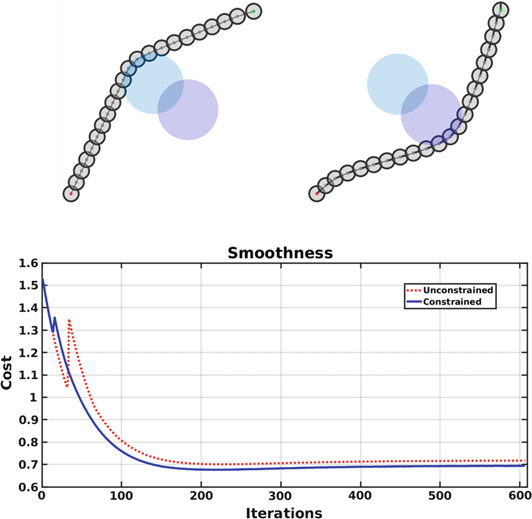
如图7所示，创建了一个简单的CHOMP和约束CHOMP的图形用户界面。在此简单设置中，我们考虑一条初始平面轨迹，该轨迹连接起始机器人位形 $(-5.0\,\text{m}, -5.0\,\text{m}, \pi/4\,\text{rad})$ 与目标位形 $(7.0\,\text{m}, 7.0\,\text{m}, \pi/2\,\text{rad})$，并初始将20个中间机器人位形堆叠在起始位形处。在连接起始和终止位形的直线中间，放置了两个障碍物，分别由半径为2 m的蓝色和紫色圆圈包围。实际上，这些圆圈的半径包含了障碍物本身的尺寸以及一定的膨胀量，即在图7中，机器人并未与实际障碍物接触。

在这些测试中，我们在相同设置下比较了无约束和有约束的CHOMP。对于两种CHOMP实现，我们使用了 $\Delta t= 1$, $\eta= 100$ 和 $\lambda= 1$。在图7c中，我们展示了每次迭代中通过无约束CHOMP以及添加滚动约束后所得到轨迹的平滑度演变情况。从图7b可以看出，添加滚动约束使我们获得的轨迹比无约束情况更平滑。在接近障碍物时，无约束轨迹表现出更急剧的转弯（见图7a），这对于重型车辆尤其不理想。此外，在有约束情况下，计算时间并未显著增加。还请注意，在本实现中我们未对最终位形施加约束，但可以采用类似的过程[9]来包含该约束。

在仿真卡车和Turtlebot上进行了另一组实验。表1展示了在模拟卡车、带拖车的仿真卡车以及Turtlebot上进行的10种不同场景的实验，这些场景从高度杂乱到稀疏杂乱不等。可以看出，由于最小转弯半径的限制，CHOMP为仿真卡车生成的轨迹完全不可行，而对Turtlebot则不然。然而，约束CHOMP能够在几乎所有所示情况下安全地行驶。同时还可以看出，在公式7中计算和更新该额外拉格朗日项并不会影响CHOMP的常规规划和更新时间。

	CHOMP Turtlebot	CHOMP 模拟AT	CHOMP 模拟AT及拖车	约束CHOMP Turtlebot	约束CHOMP 模拟AT	约束CHOMP 模拟AT及拖车
成功操作次数	8/10	3/10	1/10	10/10	9/10	7/10
平均规划时间（秒）	0.8	1.1	1.2	1.08	0.9	0.97
迭代的平均时间（秒）	41	34	25	32	29	38

7.2 洞察

从这些结果可以看出，与非完整车辆相比，约束CHOMP在差速驱动机器人上的表现更好。这是因为该方法未能完全捕捉到卡车或带拖车的卡车的所有运动学约束和物理尺寸。这种添加约束的方式看似直接且简单，但添加所有约束会使公式6及其雅可比矩阵变得更加复杂。然而，对于避免我们在测试中考虑的这类尺寸的障碍物，该方法能够提供一种快速且可行的解决方案。

在更复杂的场景中（例如，环境更杂乱或障碍物更大），应采用重新规划方案，即当CHOMP无法提供可行解时，需使用全局路径规划器重新计算一条路径。我们注意到的另一个问题是，该方法容易陷入局部极小值，但可通过随机重启[9]以及提供合适的初始轨迹输入来缓解这一问题。最后，另一种替代方案是将不等式约束引入CHOMP，以限制车辆在运动学可行区域内的运动。

8 结论

SPADES框架是为具有多个抽象层次的集装箱处理中的车队自动化而开发的。每一层都包含了精心选择的简化，以实现良好的整体系统性能，同时确保每一层都是可处理的。本文在仿真以及实际场景中测试了导航框架的底层部分。为此，我们对CHOMP算法进行了改进，使其适用于非完整车辆以及差速驱动机器人。涉及曲率约束的方法，包括采用独立的目标泛函以及与平滑性目标相结合的方式，已在[2]中进行了研究。本文研究了在CHOMP轨迹中引入滑动和滚动约束，以获得非完整车辆的平滑曲率。实验结果在实际场景和仿真中均得到了验证，自动驾驶卡车带拖车能够成功避开障碍物。研究还发现，CHOMP的基本算法无法完全捕捉车辆的运动学约束。然而，该方法在相对空旷的环境中表现令人满意。未来的工作将包括向CHOMP添加不等式约束，以及开发更先进的CHOMP版本，使其能够在更大范围内真正满足车辆的曲率约束。