题意:
已给a,b是正数, 0< a, m < 215, (a-1)2< b < a2, 0 < b, n < 231.
求:
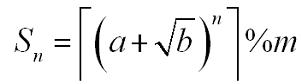
那是向上取整符号
思路:
注意到(a-1)2< b < a2
而且(a+sqrt(b))^n与其共轭式的和显然为整数,又注意到它的共轭式(a-sqrt(b))^n小于1(由于a,b大小关系)
所以即求Sn=(a+sqrt(b))^n + (a-sqrt(b))^n
再变形(易变形)递推Sn=2*aSn-1 + (b-a^2)*Sn-2 用快速幂求即可(详见http://www.klogk.com/articles/2013-06-02/hdu4565/)
//78MS 1616K 1095 B C++
#include<cstdio>
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
typedef long long ll;
ll a, b, n, mod;
struct mat
{
ll a[3][3];
mat()
{
memset(a,0,sizeof(a));
}
};
mat I;
mat mul(mat m1,mat m2)
{
mat ans;
for(int i=1;i<=2;i++)
for(int j=1;j<=2;j++)
for(int k=1;k<=2;k++)
ans.a[i][k]=(ans.a[i][k]+m1.a[i][j]*m2.a[j][k])%mod;
return ans;
}
mat quickmul(mat m,int k)
{
if(k<=0) return m;
mat ans;
for(int i=1;i<=2;i++) ans.a[i][i]=1;
while(k)
{
if(k&1) ans=mul(ans,m);
m=mul(m,m);
k>>=1;
}
return ans;
}
int main()
{
while(~scanf("%I64d%I64d%I64d%I64d",&a,&b,&n,&mod))
{
I.a[1][1]=0,I.a[1][2]=1,I.a[2][1]=((b-a*a)%mod+mod)%mod,I.a[2][2]=2*a%mod;
ll c1=2*a%mod,c2=(2*a*a+2*b)%mod;
mat t=quickmul(I,n-2);
int ans=(t.a[2][1]*c1+t.a[2][2]*c2)%mod;
if(n>2) printf("%d\n",ans);
else printf("%I64d\n",n==1? c1:c2);
}
return 0;
}
























 416
416

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








