DataWhale集成学习笔记（三）

1 训练误差与测试误差

使用训练集估计模型的参数，通常我们会在训练集上计算一些被称为训练误差的度量误差，目标是降低训练误差，原则一般都是使得我们的损失函数在训练集达到最小值，其实在实际问题中我们是可以让损失函数在训练集最小化为0。然而这样的模型是否就能达到很好的效果呢？答案是否定的。它可能对没有出现在训练集的数据的预测效果很差，因此我们希望训练得到的模型在面对未知的复杂数据时也能表现得很好。一般而言，我们并不关心模型在训练集上的训练均方误差，我们关心的是模型面对未知的样本集，即测试集上的测试误差，我们的目标是使得我们建立的模型在测试集上的测试误差最小。在先前未观测的输入上表现良好的能力被称为泛化。因此我们也希望泛化误差很低。泛化误差被定义为新输入的误差期望。
训练误差可表示为：
$$\frac{1}{m^{(train)}}{\left|\left|{\mathbf{X}}^{(train)}w-{\mathbf{y}}^{(train)}\right|\right|}_2^2$$
测试误差可表示为：
$$\frac{1}{m^{(test)}}{\left|\left|{\mathbf{X}}^{(test)}w-{\mathbf{y}}^{(test)}\right|\right|}_2^2$$

2 估计、偏差和方差

2.1 估计

我们试图通过对训练数据的学习，得到关于某个参数或者某些参数模型中的一个向量参数，将对真实参数 $\theta$ 的点估计表示为 $\hat{\theta }$。对于独立同分布的n个数据点 { x 1 , x 2 , … , x n } \{x_1,x_2,\dots,x_n\} {x1​,x2​,…,xn​}，点估计表示为这些数据的任意函数：
$$\hat{\theta }=g(x_1,x_2,\dots ,x_n)$$

2.2 偏差

估计的偏差被定义为：
$$bias({\hat{\theta }}_n)=E({\hat{\theta }}_n)-\theta$$

其中期望作用在所有数据。如果$bias({\hat{\theta }}_n)=0$，那么估计量 ${\hat{\theta }}_n$ 被称为是 无偏
，这意味着 $E({\hat{\theta }}_n)=0$。如果$limbias({\hat{\theta }}_n)=0$，那么估计量 ${\hat{\theta }}_n$ 被称为渐进无偏，这意味着 $limE({\hat{\theta }}_n)=0$。

2.3 方差

我们有时会考虑估计量的另一个性质是它作为数据样本的函数，期望的变化程度是多少。我们可以计算它的方差：
$$Var(\hat{\theta })$$
方差的平方根被称为标准差，记作$SE(\hat{\theta })$ 。估计量的方差或标准差告诉我们，当独立地从潜在的数据生成过程中重采样数据集时，如何期望估计的变化。正如我们希望估计的偏差较小，我们也希望其方差较小。

2.4 权衡偏差和方差以最小化均方误差

偏差和方差度量着估计量的两个不同误差来源。偏差度量着偏离真实函数或参数的误差期望，即刻画了学习算法本身的拟合能力。而方差度量着数据上任意特定采样可能导致的估计期望的偏差。一般来说，模型的复杂度越高，f的方差就会越大。偏差度量的是单个模型的学习能力，而方差度量的是同一个模型在不同数据集上的稳定性。
对于我们想要得到的泛化性能，是由学习算法的能力、数据的充分性以及学习任务本身的难度所共同决定的。给定学习任务，为了取得好的泛化性能，则需使偏差较小，即能够充分拟合数据，并且使方差较小，即使得数据扰动产生的影响小。
当我们可以在一个偏差更大的估计和一个方差更大的估计中进行选择时，我们最常用的方法是交叉验证。另外我们也可以比较这些估计的均方误差：
$$MSE=E[({\hat{\theta }}_n-\theta {)}^2]=Bias({\hat{\theta }}_n{)}^2+Var({\hat{\theta }}_n)$$
理想的估计是具有较小的MSE。
一般而言，增加模型的复杂度，会增加模型的方差，但是会减少模型的偏差，如图所示：

3 最小化测试误差的方法

3.1 特征提取

为了使测试误差最小，我们要对测试误差进行精确的计算，但是这很难做到，因此我们需要对测试误差进行估计。估计方式有两种：训练误差修正和交叉验证。

3.1.1 训练误差修正

模型越复杂，对训练数据的学习能力越强，训练误差越小，但是测试误差会先减后增，原因是学习能力太强，造成数据过拟合。当过拟合后，我们对特征个数进行惩罚。因此，当我们的训练误差随着特征个数的增加而减少时，惩罚项因为特征数量的增加而增大，抑制了训练误差随着特征个数的增加而无休止地减小,表示如下：
$$\begin{gathered} C_p=\frac{1}{N}(RSS+2d{\hat{\sigma }}^2) \\ RSS=\sum _{i=1}^N(y_i-\hat{f}(x_i){)}^2 \end{gathered}$$
其中d为模型特征个数；${\hat{\sigma }}^2$模型预测误差的方差的估计值，即残差的方差。

3.1.2 交叉验证

交叉验证，有的时候也称作循环估计，是一种统计学上将数据样本切割成较小子集的实用方法。在给定的建模样本中，拿出大部分样本进行建模型，留小部分样本用刚建立的模型进行预报，并求这小部分样本的预报误差，记录它们的平方加和%$C{V}_{(K)}=\frac{1}{K}\sum _{i=1}^{K}MS{E}_i$。用交叉验证的目的是为了得到可靠稳定的模型。例如5折交叉验证(5-fold cross validation)，将数据集分成五份，轮流将其中四份做训练1份做验证，5次的结果的均值作为对算法精度的估计，一般还需要进行多次5折交叉验证求均值。

交叉验证比训练误差修正的优势在于：能够给出测试误差的一个直接估计。

3.1.3 特征选择方法

• 最优子集选择
  (i) 记不含任何特征的模型为$M_0$，计算这个$M_0$的测试误差。
  (ii) 在$M_0$ 基础上增加一个变量，计算p个模型的RSS，选择RSS最小的模型记作$M_1$ ，并计算该模型$M_1$ 的测试误差。
  (iii) 再增加变量，计算p-1个模型的RSS，并选择RSS最小的模型记作$M_2$ ，并计算该模型$M_2$ 的测试误差。
  (iv) 重复以上过程知道拟合的模型有p个特征为止，并选择p+1个模型 { M 0 , M 1 , … , M p } \{M_0,M_1,\dots,M_p\} {M0​,M1​,…,Mp​} 中测试误差最小的模型作为最优模型。
• 向前逐步选择
  (i) 记不含任何特征的模型为$M_0$，计算这个$M_0$的测试误差。
  (ii) 在$M_0$基础上增加一个变量，计算p个模型的RSS，选择RSS最小的模型记作$M_1$，并计算该模型$M_1$的测试误差。
  (iii) 在最小的RSS模型下继续增加一个变量，选择RSS最小的模型记作$M_2$，并计算该模型$M_2$的测试误差。
  (iv) 以此类推，重复以上过程知道拟合的模型有p个特征为止，并选择p+1个模型 { M 0 , M 1 , … , M p } \{M_0,M_1,\dots,M_p\} {M0​,M1​,…,Mp​}中测试误差最小的模型作为最优模型。

3.2 正则化

我们还可以对模型学习的系数进行约束，这样也会提高模型的拟合能力。我们可以加入权重衰减来修改模型的训练标准。带权重衰减的线性回归最小化训练集上的均方误差和正则项的和$J(w)$。

3.2.2 L1正则化

对于L2正则化，可表示为：
$$J(w)=MS{E}_{train}+\lambda w^{\top }w$$

3.2.3 L2正则化

对于L1正则化，可表示为：
$$J(w)=MS{E}_{train}+\lambda \left|\left|w\right|\right|$$

3.3 降维

还可以将原始的特征空间投影到一个低维的空间实现变量的数量变少，如：将二维的平面投影至一维空间。机器学习领域中所谓的降维就是指采用某种映射方法，将原高维空间中的数据点映射到低维度的空间中。降维的本质是学习一个映射函数$f:x->y$，其中$x$是原始数据点的表达，目前最多使用向量表达形式。$y$是数据点映射后的低维向量表达，通常$y$的维度小于$x$的维度（当然提高维度也是可以的）。$f$可能是显式的或隐式的、线性的或非线性的。之所以使用降维是因为在原始的高维空间中，包含有冗余信息以及噪音信息，在实际应用例如图像识别中造成了误差，降低了准确率；而通过降维,我们可以减少冗余信息所造成的误差，提高识别的精度。

3.3.1 主成分分析

PCA 将输入$x$投影表示成$z$，学习数据的正交线性变换，可作为保留数据尽可能多信息的降维方法。PCA 学习一种线性投影，通过最大投影方差将原始空间进行重构，使最大方差的方向和新空间的轴对齐。

假设有一个$m\times n$ 的设计矩阵$X$，数据的均值为零，$E[x]=0$。否则对数据进行去中心化，$x_i-\bar{x}$。这样$X$对应的无偏样本协方差矩阵为：
$$Var[x]=\frac{1}{m-1}{X}^{T}X$$
PCA通过线性变换找到一个$Var[z]$是对角矩阵的表示$z=W^{T}x$。
而$X$的主成分由$X^{T}X$的特征向量给定，则：
$$X^{T}X=W\Lambda W^T.$$
最大投影方差的步骤：
(i) 中心化： $x_i-\bar{x}$
(ii) 计算每个点 $x_1,\dots ,x_n$至 ${\vec{u}}_1$ 方向上的投影： $(x_i-\bar{x}){\vec{u}}_1,||{\vec{u}}_1||=1$
(iii) 计算投影方差：$J=\frac{1}{N}\sum _{i=1}^N[(x_i-\bar{x}{)}^T{\vec{u}}_1{]}^2,||{\vec{u}}_1||=1$
(iv) 最大化投影方差求 𝑢⃗ 1 ：
$$\begin{gathered} {\bar{u}}_1=argma{x}_{u_1}\frac{1}{N}\sum _{i=1}^N[(x_i-\bar{x}{)}^T{\vec{u}}_1{]}^2 \\ s.t.{\vec{u}}_1^T{\vec{u}}_1=1({\vec{u}}_1往后不带向量符号) \end{gathered}$$

得到：
$$\begin{gathered} J=\frac{1}{N}\sum _{i=1}^N[(x_i-\bar{x}{)}^T{\vec{u}}_1{]}^2=\frac{1}{N}\sum _{i=1}^N[u_1^T(x_i-\bar{x})(x_i-\bar{x}{)}^T{u}_1] \\ =u_1^T[\frac{1}{N}\sum _{i=1}^N(x_i-\bar{x})(x_i-\bar{x}{)}^T]u_1=u_1^T{S}^2{u}_1 \end{gathered}$$

即：
$$\begin{gathered} {\hat{u}}_1=argma{x}_{u_1}{u}_1^T{S}^2{u}_1,s.t.u_1^T{u}_1=1 \\ L(u_1,\lambda )=u_1^T{S}^2{u}_1+\lambda (1-u_1^T{u}_1) \\ \frac{\partial L}{\partial u_1}=2S^2{u}_1-2\lambda u_1=0 \\ 即：S^2{u}_1=\lambda u_1 \end{gathered}$$
可以看到： $\lambda$为 $S^2$的特征值，$u_1$为$S^2$的特征向量。因此我们只需要对中心化后的协方差矩阵进行特征值分解，得到的特征向量即为投影方向。如果需要进行降维，那么只需要取p的前M个特征向量即可。

4 模型超参数调优

4.1 参数

机器学习中的参数是指模型参数，它不是人为指定的，是模型内部的配置变量，可以用数据估计模型参数的值。可以通过对训练数据的学习，对模型的优化学习得到。例如支持向量机中的支持向量、神经网络中的权值等。它们通常被保存为模型的一部分。

• 进行预测时需要参数。
• 它参数定义了可使用的模型。
• 参数是从数据估计或获悉的。
• 参数通常不由编程者手动设置。
• 参数通常被保存为学习模型的一部分。
• 参数是机器学习算法的关键，它们通常由过去的训练数据中总结得出 。

4.2 超参数

模型超参数是模型外部的配置，必须手动设置参数的值。一个参数被设置为超参数一方面是因为它太难优化了；更多的是因为它不适合在训练集上学习，所以该选项必须为超参数。

• 超参数通常用于帮助估计模型参数。
• 超参数通常由人工指定。
• 超参数通常可以使用启发式设置。
• 超参数经常被调整为给定的预测建模问题。

4.3 超参数调优

那么如何通过取不同的超参数的值，来提升模型的性能呢？

4.3.1 网格搜索GridSearchCV()

sklearn官网介绍
网格搜索的思想是对所有需要优化的超参数的选择项进行排列组合，对每一个组合训练一个模型，然后选择对应模型测试误差最小的超参数组合。我们从超参数空间中寻找最优的超参数，很像从一个网格中找到一个最优的节点，因此叫网格搜索。网格搜索相当于暴力地从参数空间中每个都尝试一遍，然后选择最优的那组参数。
使用网格搜索结合Pipeline

sklearn.model_selection.GridSearchCV(estimator, param_grid, *, scoring=None, n_jobs=None, refit=True, cv=None, verbose=0, pre_dispatch='2*n_jobs', error_score=nan, return_train_score=False)

# 我们先来对未调参的SVR进行评价：
boston = datasets.load_boston()     # 返回一个类似于字典的类
X = boston.data
y = boston.target
features = boston.feature_names
pipe_SVR = make_pipeline(StandardScaler(),
                                                         SVR())
score1 = cross_val_score(estimator=pipe_SVR,
                                                     X = X,
                                                     y = y,
                                                     scoring = 'r2',
                                                      cv = 10)       # 10折交叉验证
print("CV accuracy: %.3f +/- %.3f" % ((np.mean(score1)),np.std(score1)))

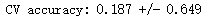
# 下面我们使用网格搜索来对SVR调参：
from sklearn.pipeline import Pipeline
pipe_svr = Pipeline([("StandardScaler",StandardScaler()),
                                                         ("svr",SVR())])
param_range = [0.0001,0.001,0.01,0.1,1.0,10.0,100.0,1000.0]
param_grid = [{"svr__C":param_range,"svr__kernel":["linear"]},  # 注意__是指两个下划线，一个下划线会报错的
                            {"svr__C":param_range,"svr__gamma":param_range,"svr__kernel":["rbf"]}]
gs = GridSearchCV(estimator=pipe_svr,
                                                     param_grid = param_grid,
                                                     scoring = 'r2',
                                                      cv = 10)       # 10折交叉验证
gs = gs.fit(X,y)
print("网格搜索最优得分：",gs.best_score_)
print("网格搜索最优参数组合：\n",gs.best_params_)

4.3.2 随机搜索RandomizedSearchCV()

sklearn官网介绍
由于随着参数类别个数的增加，网格搜索需要尝试的次数呈指数级增长。那么这一问题该如何解决呢？那就是使用随机搜索。参数的随机搜索中的每个参数都是从可能的参数值的分布中采样的。

sklearn.model_selection.RandomizedSearchCV(estimator, param_distributions, *, n_iter=10, scoring=None, n_jobs=None, refit=True, cv=None, verbose=0, pre_dispatch='2*n_jobs', random_state=None, error_score=nan, return_train_score=False)