关于PA匹配和LNA匹配的理解

硬件老钢丝

已于 2022-05-06 16:57:15 修改

阅读量1.3w

点赞数 58

分类专栏：常规功放设计 ADS小技巧 LNA设计专栏文章标签：匹配设计 ADS小技巧

于 2022-05-04 21:24:55 首次发布

本文链接：https://blog.csdn.net/kexuedalao/article/details/124565430

版权

常规功放设计同时被 3 个专栏收录

17 篇文章

订阅专栏

ADS小技巧

9 篇文章

订阅专栏

LNA设计专栏

6 篇文章

订阅专栏

文章目录

前言
一、LNA匹配
二、PA匹配
总结

前言

在做PA设计和LNA设计时，其在设计中主要会考虑到匹配网络的设计，PA通常采用共轭匹配，而LNA的匹配则相对较复杂，这里完全取决于你采用什么阻抗去进行匹配。下面我们将主要针对这两种情况进行说明。
下图是有源电路的基本匹配网络方向。
在这里插入图片描述

图1 匹配方向图

Zs和ZL分别是PA在负载牵引和源牵引得到的值，方向指向端口方向；
Zin和Zout可以视为S11和S22阻抗。

一、LNA匹配

LNA的匹配可以归结为两种，一种是S参数匹配，一种是共轭匹配。下面详细概述。
对于LNA的输入匹配，其通常是希望满足最小噪声匹配，但考虑到以最小噪声匹配时，S11通常会不好，除非你的Ga_circle和Ns_circle是几乎重合，否则S参数一般是不好的，这个时候就需要我们去考虑到底选用怎样一种匹配是可以达到好的要求。
首先，在仿真LNA时，以笔者设计为例，加入如下图所示控件。

1、控件部署

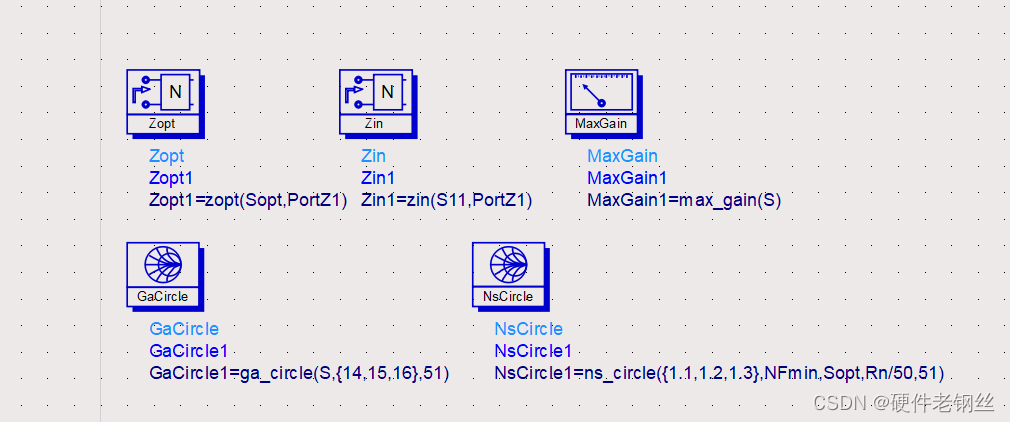
在这里插入图片描述

图2 控件图

Zopt1返回的数据是最佳噪声，一般用圆图显示比较好。
Zin1返回是的S11参数，也就是标记端口的阻抗值，可以用圆图或者数据表的形式来显示。如果想看2端口的S参数，S11变为S22，如果存在多个zin控件，记得更改为Zin2或者Zin3。
Maxgain为最大增益。
GaCircle为这里的输入增益圆，我这里选择看增益为14、15、16的圆
NsCircle为输入噪声系数圆，在初步仿真后我知道我的NFmin为1.006，所以我这里选择看nf(2)为1.1、1.2、1.3的圆，读者也可以根据自己的设计选择圆。

2、仿真结果和仿真结果

在部署完上述控件后，仿真电路和仿真结果如下图所示。
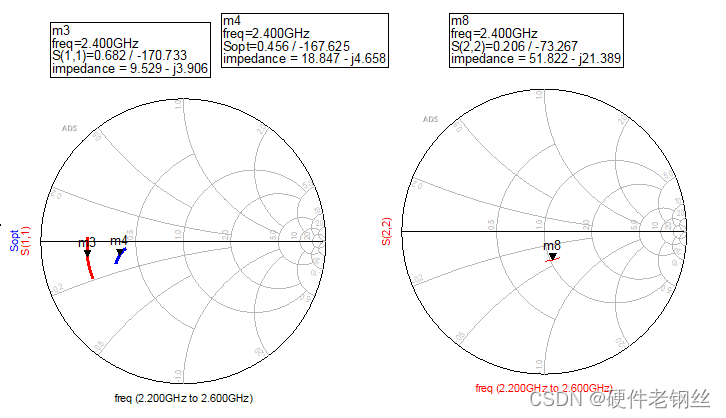
在这里插入图片描述

图3 电路结构图

在这里插入图片描述

图4 S参数和Sopt圆图显示

在这里插入图片描述

图5 最大增益和S21

在这里插入图片描述

图6 NFmin和nf(2)

在这里插入图片描述

图7 GaCircle和NsCircle圆图

3、结果分析

对于图4，我们得到中心频点的S11为9.53-j3.9，Sopt为18.85-j4.66，S22为51.8-j*21.4。
这里得到的曲线是是2.2GHz-2.6GHz范围内的曲线，首先我们要知道匹配的方向。S11得到的阻抗方向是指向晶体管的，而Sopt的方向是指向端口的，用一个最简单的方式去判断匹配是否要共轭，对于最简单的阶梯阻抗变换线，如下图所以，我们知道如果从左向右匹配，最后得到得阻抗方向向右，同理，如果从右往左匹配方向指向左边。
在这里插入图片描述

图8 用阶梯阻抗变换线表明匹配方向

S11匹配

如果我们采用S11阻抗进行匹配，他代表着“最大”增益匹配，在匹配时，我们是从输入端口匹配到左边的Port1，方向向左，而此时的S11方向是指向右边，所以要变成共轭进行匹配。我们直接将图3中的端口1变成S11共轭进行观察。得到下面的结果。
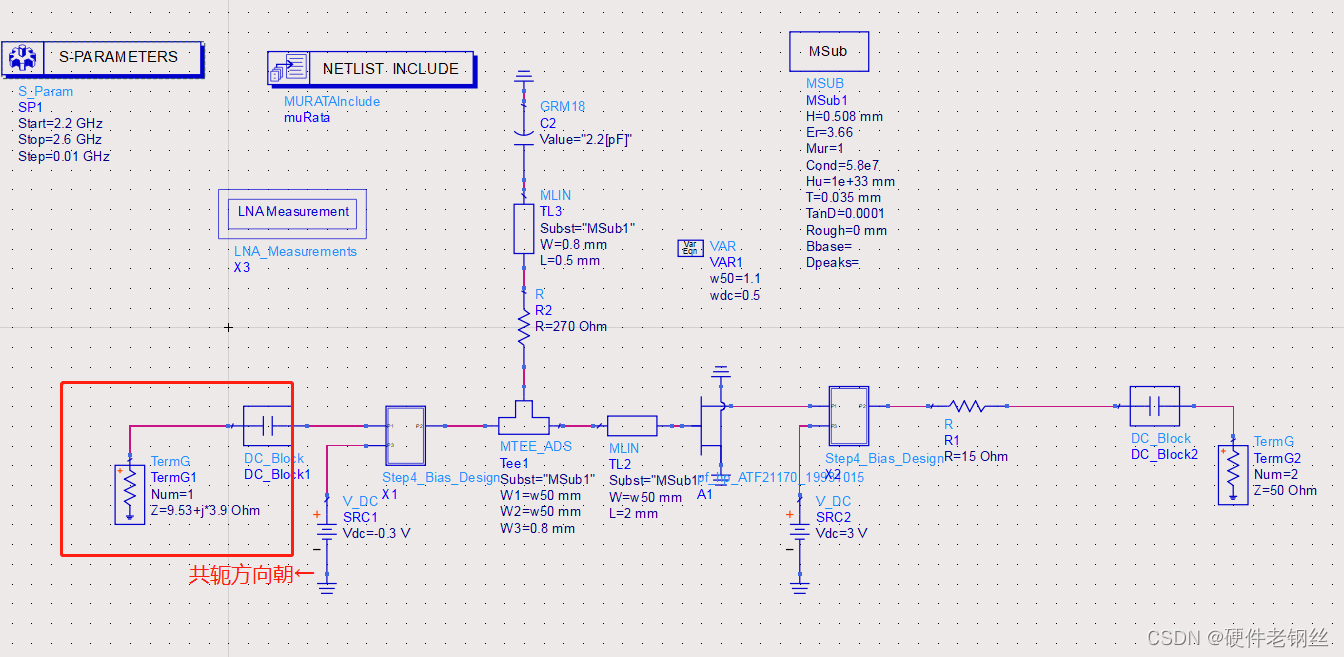
在这里插入图片描述

图9 变换端口1为S11共轭

在这里插入图片描述

图10 匹配完后的S11

可以看到按S11匹配后落到了中心位置，当然这是因为参考阻抗变成了现在的阻抗，不是50欧姆的参考阻抗了。
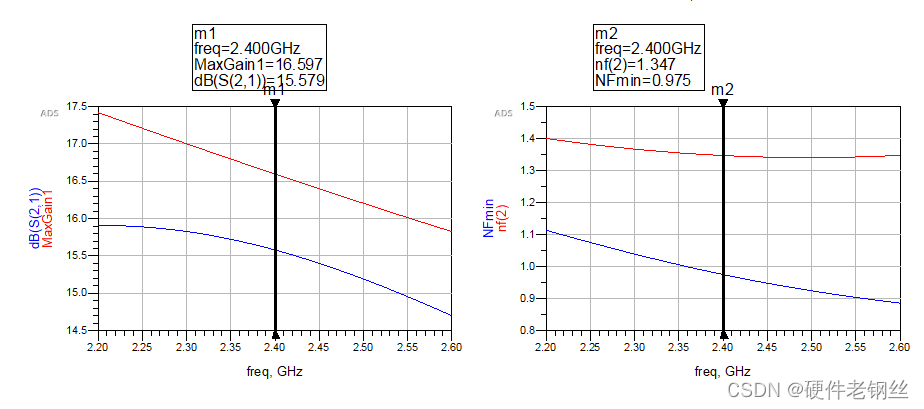
在这里插入图片描述

图11 S11匹配结果

在这里插入图片描述

图12 匹配过后的增益和噪声

从图中可以看出，在按S11匹配后，增益得到了很大的提升，噪声系数变化不大，如果说现在得到的nf(2)是满足我们最后的需求，那么用S11匹配即可。

Sopt匹配

Sopt阻抗是最佳噪声阻抗，其方向相当于图1中的Zs方向，所以在以Sopt阻抗匹配时，方向一致，不需要进行共轭，匹配过程下图所示。

在这里插入图片描述

图13 Sopt匹配

在这里插入图片描述

图14 Sopt 匹配结果

在这里插入图片描述

图15 S11结果

很明显，以最小噪声匹配时，S11结果是很差的
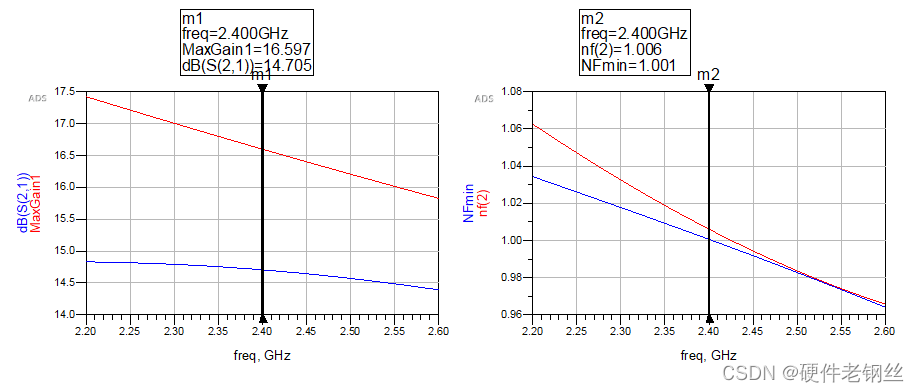
在这里插入图片描述

图16 增益和噪声匹配结果

在对Sopt匹配匹配之后，可以看到中心频点的NFmin和nf(2)几乎要重合了，也表明了匹配方向的正确性。
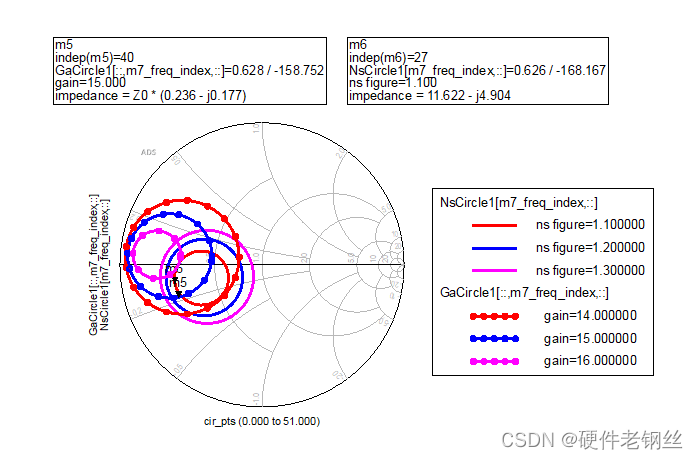
但是综合来看，输入匹配最好不好按Sopt来匹配，S11反正更好，为了折中增益和噪声系数，我们可以用图7所示的增益圆和噪声圆，这个值的方向是和Zs方向一致。
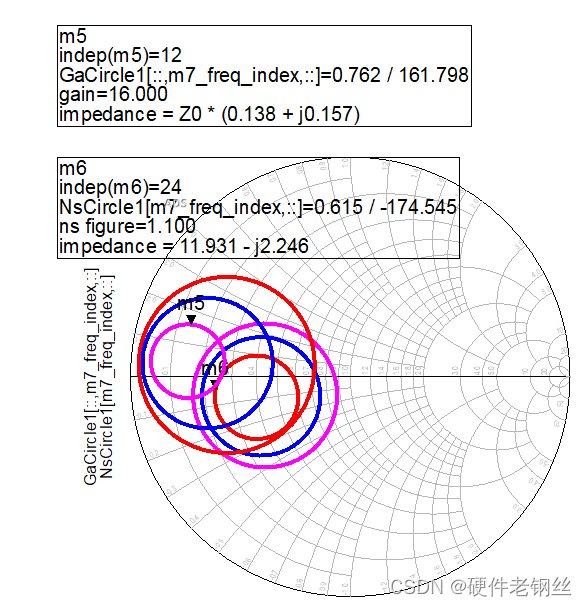
在这里插入图片描述

图17 噪声和增益圆

利用该图选点去进行匹配，有时候得到的S参数依旧不好，我们尽量选择点靠近最大增益的阻抗点，如果还不好可以采用自动优化的方式进行优化设计。
下面我们取了一个值，在Smith Chart中进行匹配，注意，在控件中的值，是本来取得值，ZS方向和匹配方向相同所以不需要共轭。
在这里插入图片描述

图18 Smith Chart匹配示意图

S22匹配

得到S22阻抗为51.8-j*22，同理其匹配的时候，由于是向右匹配，S22方向向左，所以要变成共轭匹配。在用控件匹配时，要注意一点。如下图所示，在控件中进行匹配时，默认都是从ZL开始匹配，也就是从50匹配到我们S22，整体方向向左，而S22方向本身就是向左，但是Zs上面有一个共轭符号，所以这里要给他变成共轭值，共轭的共轭就是S22本身的值。
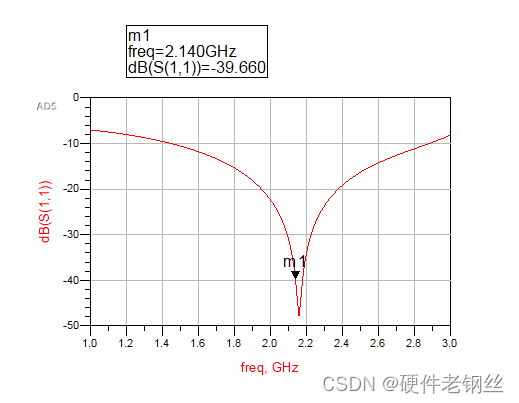
在这里插入图片描述