对于需要迭代计算的算法,MapReduce显然不可用,迭代n次的IO量太大,而基于消息的传递模型,BSP和MPI的优势就出来了。BSP的编程模型,试验过了,确实容易入门,只要将求解问题(例如,优化问题、图的最短路径问题等等)抽象成图模型(顶点Vertex、边Edge)后,再通过消息Message,来不断迭代求解即可。拿前面有篇文章,NMF的矩阵分解这个优化问题,来实验:
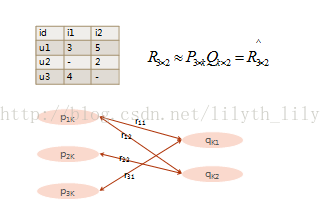
1)NMF的矩阵分解基本思想:用分解后的两个矩阵P、Q乘积,来逼近原始矩阵R,越逼近越好。这里,采用L2正则避免过拟合。
2)选定优化方法,将问题抽象成图模型,采用BSP编程模型求解。这里选用批量梯度下降,将待求解问题抽象成顶点、边,举例如下,设用户数m,item数n,k是分解后的m的维数,ks是原始稀疏矩阵的非空元素的个数。则抽象后的节点个数m+n,边数ks。其中,r_ij的值是存储到图的边上。
3)上面的图模型抽象好后,用批量梯度下降来迭代求解这个最优化问题。例如,求p矩阵中每个元素值如下公式,每次迭代更新时就用下面第二个公式。求解q类似,公式略。
4)选定步长0.002试验








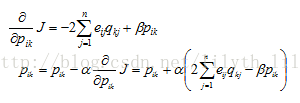
















 1722
1722

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








