强化学习系列14：动态规划求解法

本文是强化学习系列1的举例补充。这里介绍可以求解连续决策问题的动态规划问题。

1. 关于动态规划

动态规划将状态对应的值记录了下来，可以避免重复计算；这是它和Divide and Conquer最大的区别。两者都是树搜索的过程，但是Divide and Conquer没有使用值函数的步骤，因此如果可以的话，尽量使用动态规划求解。
动态规划要求问题是马尔科夫决策过程（Markov Decision Process，MDP），核心即每一阶段的决策过程不依赖于以往的状态。
下面使用Fibonacci来进行对比
递归法如下：

def fib(n):
  if n <= 0: # base case 1
    return 0
  if n <= 1: # base case 2
    return 1
  else: # recursive step
    return fib(n-1) + fib(n-2)

而DP法如下：

calculated = {}

def fib(n):
  if n == 0: # base case 1
    return 0
  if n == 1: # base case 2
    return 1
  elif n in calculated:
    return calculated[n]
  else: # recursive step
    calculated[n] = fib(n-1) + fib(n-2)
    return calculated[n]

更常见的是使用bottomUp：

def fib(n):
  if n == 0:
    return 0
  if n == 1:
    return 1
  # table for tabulation
  table = [None] * (n+1) 
  table[0] = 0        # base case 1, fib(0) = 0
  table[1] = 1        # base case 2, fib(1) = 1
  # filling up tabulation table starting from 2 and going upto n
  for i in range(2,n+1):  
    # we have result of i-1 and i-2 available because these had been evaluated already
    table[i] = table[i-1] + table[i-2]  
  # return the value of n in tabulation table
  return table[n]

2. 练习

2.1 背包问题

背包问题是个典型的整数规划问题，可以用Divide and Conquer树进行搜索。我们尝试在搜索过程中加上状态存储，即使用topDown方法求解。阶段定义为：第i个物品；状态定义为：剩余容量；决策定义为：是否采用第i个物品。

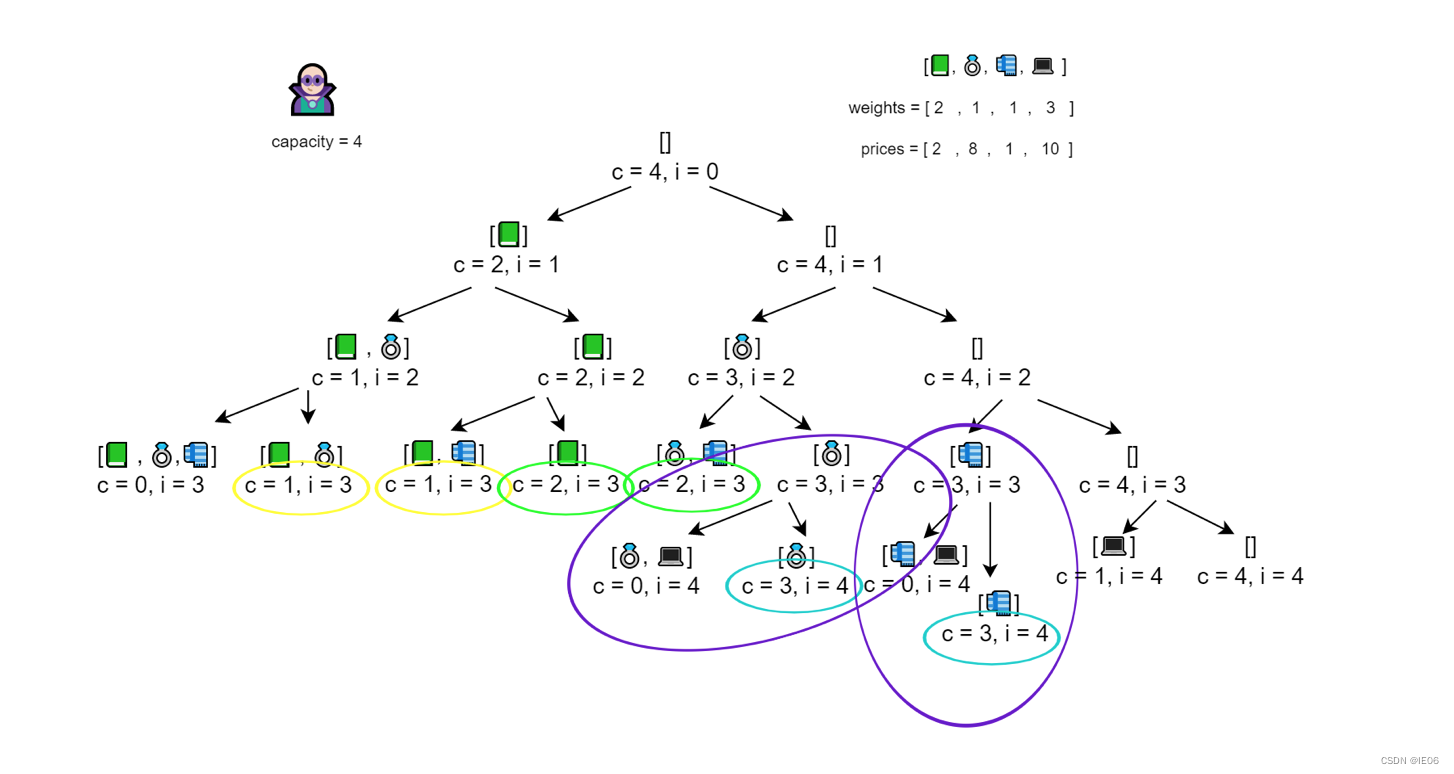
在上面的例子中，总共有4个物品，因此总共有4阶段。注意观察画圈的部分，可重复利用。

2.2 换零钱问题

bills：零钱额度清单，例如[1,2,5]代表有1元，2元和5元三种额度。
amount：待换额度，例如5代表要换5元。
那么迭代法为：

def countways_(bills, amount, index):
  if amount == 0:     # base case 1
    return 1
  if amount < 0 or index >= len(bills):      # base case 2
    return 0
  # count the number of ways to make amount by including bills[index] and excluding bills[index]
  return countways_(bills, amount - bills[index], index) + countways_(bills, amount, index+1)

def countways(bills, amount):
  return countways_(bills, amount, 0)

print(countways([5,2,1], 5))

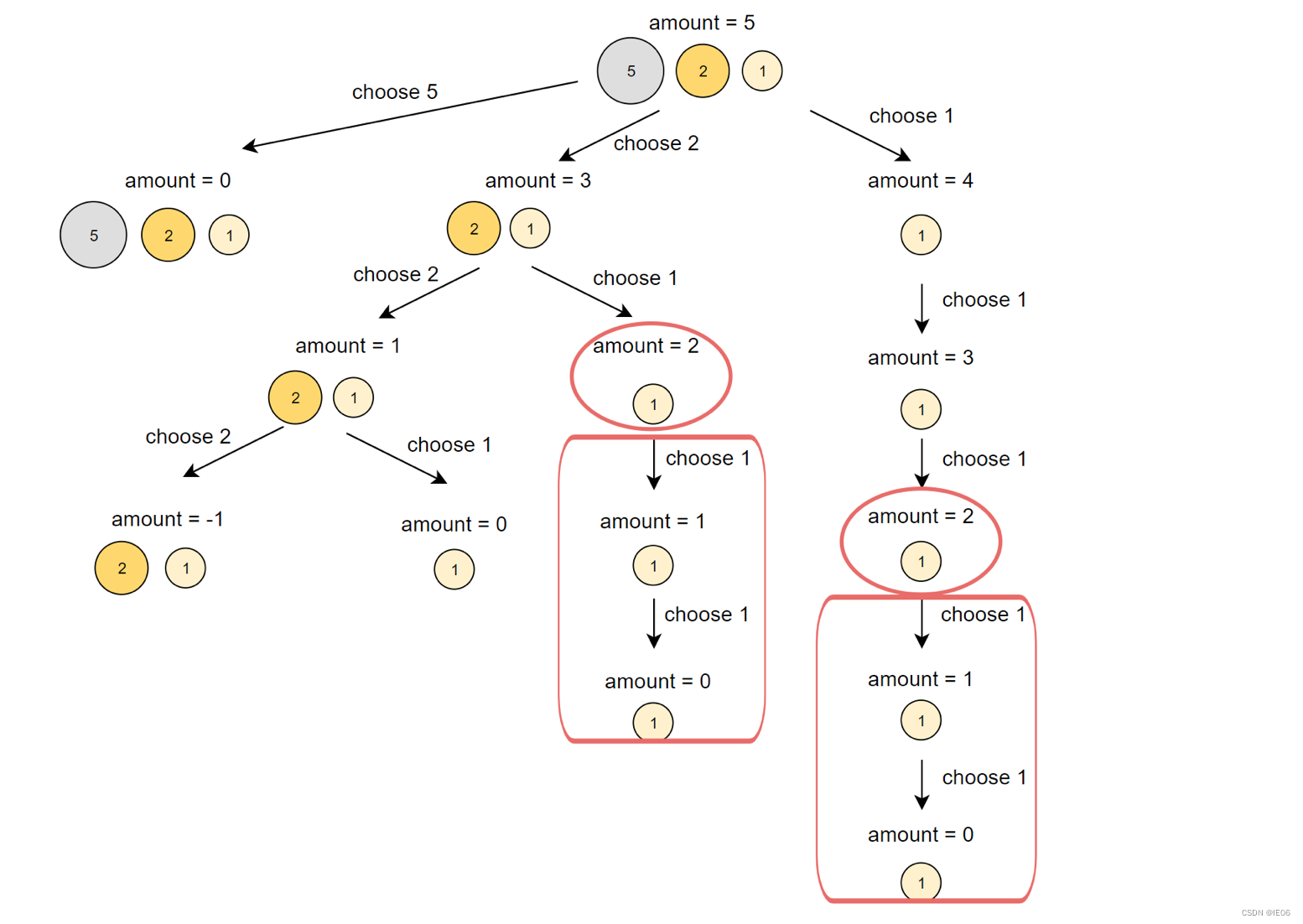
上图展示了使用topdown法的图示。
下面使用bottomup法进行求解，需要使用到lookuptable，记作dp。它是一张二维表，横坐标为bills的id，纵坐标为剩余待换零钱量。

def countways(bills, amount):
  if amount <= 0:
    return 0 # 终止条件
  dp = [[1 for _ in range(len(bills))] for _ in range(amount + 1)]
  for amt in range(1, amount+1): # 剩余待换数量
    for j in range(len(bills)): # 允许使用的id为j～n
      bill = bills[j]
      if amt - bill >= 0:
        x = dp[amt - bill][j] # x为继续使用一张j
      else:
        x = 0
      if j >= 1: # y为拓展允许使用的id为j-1～n
        y = dp[amt][j-1]
      else:
        y = 0
      dp[amt][j] = x + y
  return dp[amount][len(bills) - 1]

print(countways([1,2,5], 5))

3. 一些优化方法

观察2.1节的背包问题，我们将其建立成了连续决策问题，一共4个阶段，并满足1. 最优子结构性质；2. 决策和历史状态无关。
这里再举一个最大流问题：

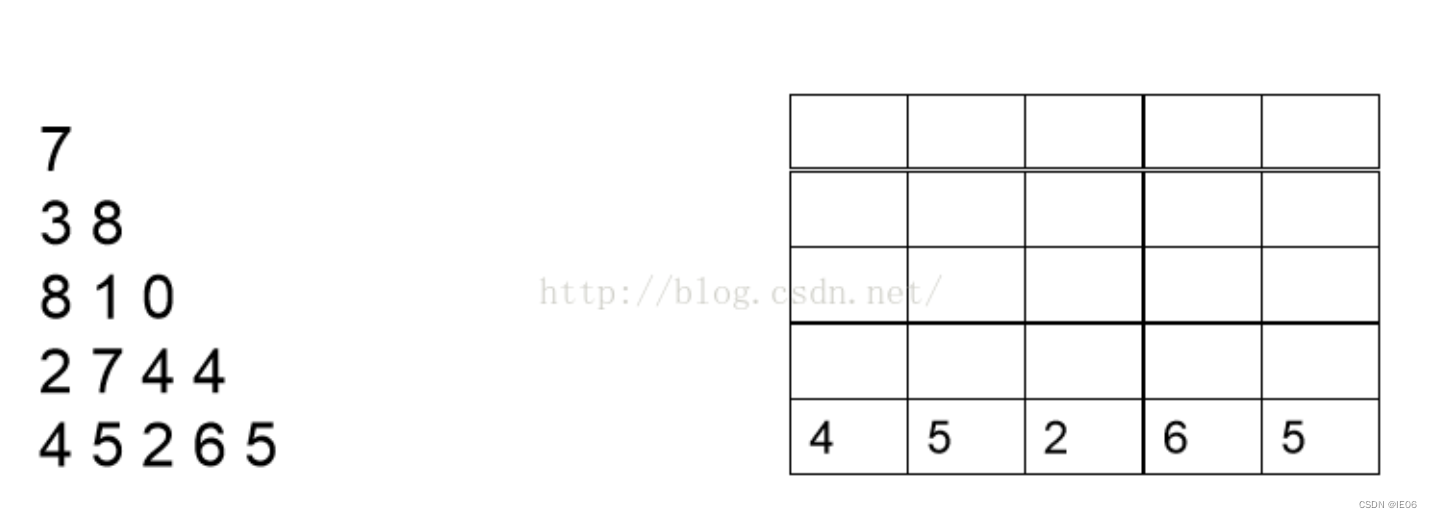
在上面的数字三角形中寻找一条从顶部到底边的路径，使得路径上所经过的数字之和最大。路径上的每一步都只能往左下或右下走。
问题拥有非常直观的有5个阶段，并拥有最优子结构和历史无关性，使用bottomup的方法，lookup表的值为决策数之和（value），纵坐标为阶段（stage），横坐标为选择第几个数（即action）。

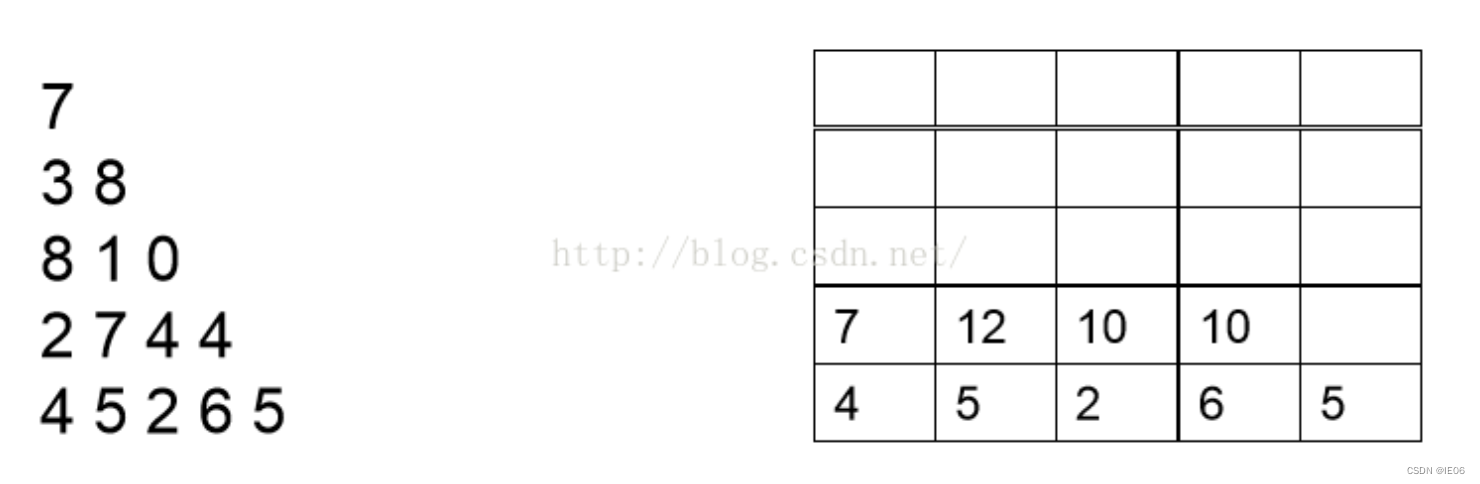
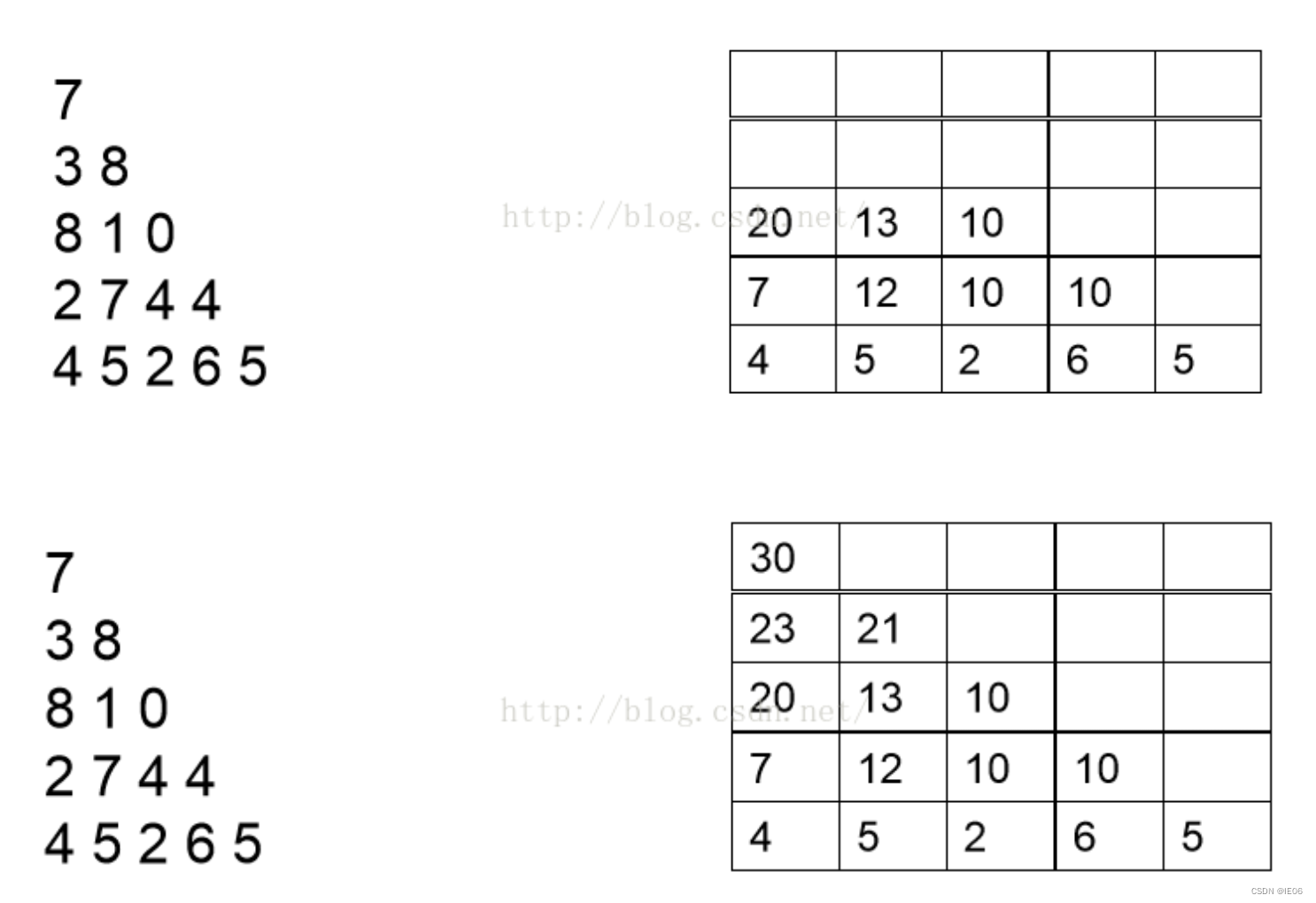
这是个经典的DP求解连续决策问题的案例，子问题是从后向前求解的。

还有一种更省空间的方法，即只使用一维数组：