Python系动--绘制洛伦兹吸引子

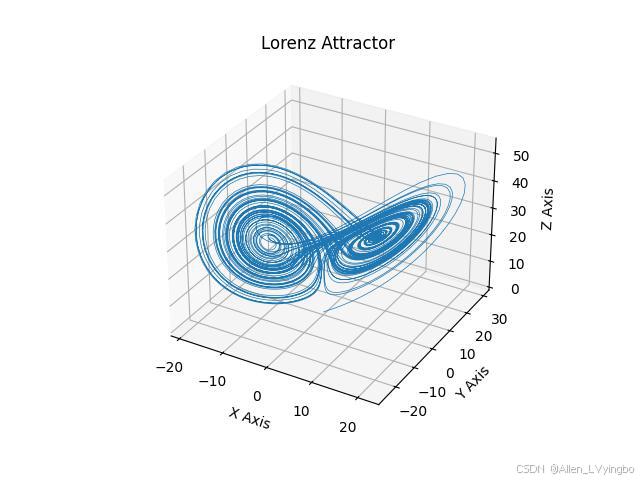
Python画出洛伦兹吸引子的图像： 使用matplotlib库和numpy库来绘制洛伦兹吸引子的图像。下面是绘制洛伦兹吸引子图像

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
import numpy as np

# 洛伦兹系统参数
sigma = 10.0
rho = 28.0
beta = 8.0 / 3.0

# 洛伦兹系统方程
def lorentz_system(x, y, z, sigma, rho, beta):
    dx = sigma * (y - x)
    dy = x * (rho - z) - y
    dz = x * y - beta * z
    return dx, dy, dz

# 时间步长和迭代次数
dt = 0.01
N = 10000

# 初始化变量
x = np.empty(N)
y = np.empty(N)
z = np.empty(N)

# 初始条件
x[0], y[0], z[0] = (0.1, 0.0, 0.0)

# 时间演化
for i in range(N - 1):
    dx, dy, dz = lorentz_system(x[i], y[i], z[i], sigma, rho, beta)
    x[i + 1] = x[i] + (dx * dt)
    y[i + 1] = y[i] + (dy * dt)
    z[i + 1] = z[i] + (dz * dt)

# 绘制图像
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot(x, y, z, lw=0.5)
ax.set_xlabel("X Axis")
ax.set_ylabel("Y Axis")
ax.set_zlabel("Z Axis")
ax.set_title("Lorenz Attractor")
plt.show()

在医学系统工程学中，奇异吸引子的概念和特性可以应用于多个方面，以下是一些具体的应用场景：

1. 系统稳定性分析：

   • 混沌控制：在工程系统中，混沌现象可能会导致系统的不稳定和不可预测性。通过识别奇异吸引子，工程师可以设计控制策略来避免或减少混沌行为，从而提高系统的稳定性。
   • 故障检测：奇异吸引子可以揭示系统行为的变化，这有助于在系统出现故障或异常时进行早期检测。

2. 系统设计与优化：

   • 参数调优：奇异吸引子对系统参数非常敏感，这可以用于指导工程师如何调整系统参数以实现所需的性能。
   • 非线性动力学建模：在系统设计过程中，奇异吸引子的特性可以帮助工程师更好地理解和模拟系统的非线性动力学行为。

3. 控制系统设计：

   • 控制器设计：奇异吸引子提供了系统动态行为的详细视图，这对于设计高级控制器（如自适应控制器、滑模控制器）至关重要。
   • 预测控制：在预测控制中，对系统未来行为的准确预测是关键。奇异吸引子的知识可以帮助改善预测模型的准确性。

4. 时间序列分析：

   • 信号处理：奇异吸引子可以用于分析时间序列数据，以识别隐藏的模式和趋势，这在信号处理和通信系统中非常有用。

5. 复杂网络分析：

   • 网络同步：在复杂网络中，理解节点之间的动态关系对于实现网络同步至关重要。奇异吸引子的概念有助于分析网络中的同步行为。

6. 模式识别与机器学习：

   • 特征提取：奇异吸引子的特性可以用于从复杂系统数据中提取有用的特征，这对于模式识别和机器学习任务很有帮助。

7. 医疗能源系统：

   • 电力系统稳定性：在电力系统中，奇异吸引子的分析可以帮助评估系统的稳定性和响应能力，特别是在面对突发事件（如短路、负载变化）时。